Рассмотрим световой поток, излучаемый элементарной площадкой, находящейся на оптической оси системы и перпендикулярной к ней
Лекция 10
Световой поток, проходящий через оптическую систему.
Освещенность изображения.
Рассмотрим световой поток, излучаемый элементарной площадкой, находящейся на оптической оси системы и перпендикулярной к ней.
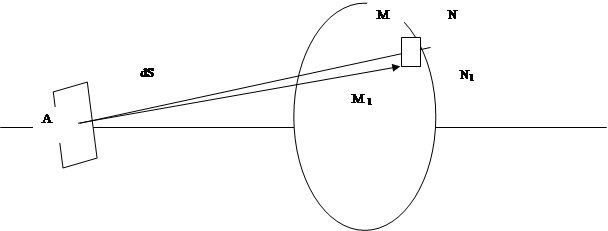

Величина светового потока dФ, входящего во входной зрачок ОС определяется следующим образом.
Световой поток d2 Ф, падающий на элементарную площадку dS1 на входном зрачке, равен d2 Ф=Idw;
подставим выражение для силы света I= LdScoss; где dS – площадь элементарной излучающей площадки,
d2 Ф =LdScossdw;
телесный угол dw определяется как
dw = sinsdS1 /r2 ,
где dS1 – площадь элементарной площадке в плоскости входного зрачка,
r – расстояние от этой площадки до точки А.
Площадь dS1 = MM1 *MN . Тогда выражение для dw можно записать в следующем виде:
MM1 MN
dw= ¾ * ¾ * sins =dsdj sins.
r r
Поток, падающий на площадку:
d2 Ф == LdScoss sins dsdj.
Для того чтобы определить весь поток, входящий во входной зрачок, необходимо провести интегрирование по плоскости входного зрачка, т.е. по углу dj, и по углу ds.
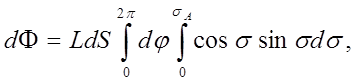
где sА - апертурный угол. Проведя интегрирование, получаем:
d Ф = p LdSsin2 sA ,
Аналогично для пространства изображений можно записать:
d Ф’= p L’dS’sin2 s’A’
где dS’–элементарная площадка, сопряженная с dS.
Яркости предмета и изображения связаны законом Кирхгофа
L’=t (n’/n)2 L, где t- коэффициент пропускания ОС. Тогда
d Ф’= p t (n’/n)2 LdS’sin2 s’A’ (1)
Найти поток можно, используя закон сохранения энергии:
d Ф’= t dФ = p t LdS sin2 sA . (2)
Освещенность изображения
E’=d Ф’/dS’= p t LdS sin2 sA /dS’ .
Площадки dS и dS’ сопряженные, а значит и подобные, поэтому отношение их площадей равно квадрату отношения их линейных размеров, отношение линейных размеров – это, по определению, линейное увеличение, т.е.
E’= p t L (sin sA /b)2 .
Если взять из d Ф’ формулы (1): E’= p t (n’/n)2 L sin2 s’A’ .
Приравняем правые части, сократим: b=nsinsA / n’sins’A’ .
Это выражение носит название закона синусов. Закон синусов является необходимым условием существования совершенного изображения малого участка плоскости, близкого к оптической оси и перпендикулярного ей. Закон синусов можно записать в следующем виде:
n’y’sins’= nysins .
Это выражение является инвариантом для реальной ОС. Сравнивая его с инвариантом Лагранжа-Геймгольца видим, что они совпадают при малых апертурных углах.
Рассмотрим элементарную площадку вне оси.
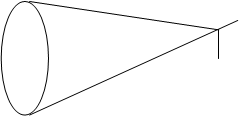

d Ф’= p L’dS’ sin2 A’/2 . E’/E’0 = sin2 ( A’/2)/ sin2 s’A’ .
Исследование этой формулы показывает, что для систем с относительным отверстием 1:3,5 и ниже ее можно упростить следующим образом:
E’/E’0 =cos4 w’.
При наличии в ОС виньетирования : E’ = k S E’0 cos4 w’.
.
Закон косинусов
N’dl’cose’ - ndlcose =dС, - закон косинусов.
Рассмотрим частные случаи.
1. Пусть точка О1 находится на оптической оси, отрезок перпендикулярен оптической оси. Тогда e=900 -s; e’=900 -s’,
n’dl’sins’ - ndlsins = dC.
Если луч идет по оптической оси s=s'=0, а значит dC =0
n’dl’sins’ = ndlsins .
Получили уже известный нам закон синусов.
2. Найдем условие получения совершенного изображения участка оптической оси реальной оптической системы. e = s; e’ = s’; dl=dz; dl’=dz’:
n’dz’coss’- ndzcoss =dC; разделим обе части на dz и обозначим dC/dz через новую постоянную С1,:
n’dz’coss’/ dz - ncoss =C1 .
Значение С1 определим положив s=s'=0:
C1 =n’a - n; тогда получим:
n’a(1-coss’)=n(1-coss);
n’asin2 s’/2=nsin2 s/2 - условие Гершеля.
Лекция 11
Аберрации оптических систем
Нарушение гомоцентричности пучков лучей оптическими системами называют погрешностями или аберрациями. Аберрации представляют в виде волновых аберраций и в виде геометрических аберраций.
Волновые аберрации
R2 –r1 =(1-n2 )d/n2 .
Это условие носит название условия ахроматизации мениска Максутова. d>0, (1- n2 )<0, (r2 –r1) <0, в этом случае мы имеем отрицательную линзу.
Для предмета, находящегося на конечном расстоянии, продифференцируем формулу отрезков:
1/a’ –1/a=1/f’; a=cons;
da’= dSхр’ = - a’2 /(nf’); a’=(1-b)f’; dS’=-(1- b)2 f’/n.
При b = –1, когда предмет и его изображение находятся на двойном фокусном расстоянии от оптической системы, dSхр’= - 4 f’/n.
Кроме частного случая, мениска Максутова, простейшей оптической системой, позволяющей устранить хроматизм положения, является двухлинзовый склеенный объектив. Оптические силы линз определяются из совместного решения условия масштаба и условия ахроматизации:
F1 +F2 =1; F1 /n1 +F2 /n2 = 0.
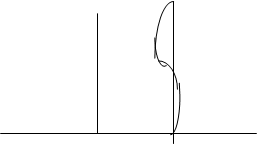
Если dS’l1=dS’l2, то dS’= 0 .В этом случае график зависимости S’ от l имеет дугообразный вид.
 l
l
0 S’,
Оптическая система, в которой для двух длин волн устранен хроматизм положения, называется ахроматом.
Остаточная хроматическая аберрация называется вторичным спектром. Стрелка дуги кривой хроматизма положения характеризует величину вторичного спектра. Величина вторичного спектра 2-х линзового склеенного объектива для предмета, находящегося на бесконечности равна:
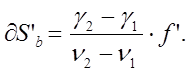
В особых случаях добиваются равенства нулю хроматизма положения для 3-х длин волн.
 l,
l,
S’
Оптическая система, в которой хроматизм положения исправлен для трех длин волн, называется апохроматом.
Если в оптической системе устранен хроматизм положения, то этим не обеспечивается отсутствие окраски в изображении, т.к. линейное увеличение является функцией показателей преломления:
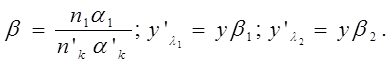 |
Вследствии наложения изображений разной величины на краях изображения появляется цветная кайма.
Изменение величины изображения для различных длин волн называется хроматизмом увеличения.
db=bl1 –bl2 или dy’= y’l1 –y’l2 .
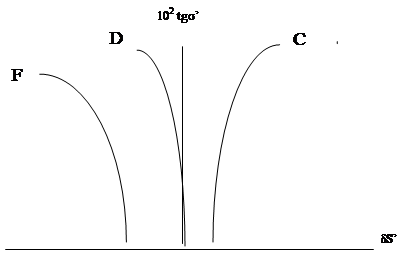
Хроматическая аберрация пучка лучей, выходящих из точки предмета, находящейся на оптической оси, называется сферохроматической аберрацией. Она равна разности сферических аберраций для данных длин волн.
Для характеристики сферохроматической аберрации строят графики сферической аберрации для длин волн, для которых исправляется хроматизм положения, и для основной длины волны, для которой коррегируются монохроматические аберрации.
Лекция 13