ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. ЭКСТЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. ЭКСТЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ - Лекция, раздел Философия, Лекция 13 ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ План 8. Введение. 9. Частные Производные...
ПЛАН
8. Введение.
9. Частные производные высших порядков.
10. Экстремумы функции двух переменных.
11. Наибольшее и наименьшее значение функции в замкнутой области.
12. Подбор параметров для эмпирических формул простейшего вида по методу наименьших квадратов
13. Заключение.
17.1. Введение
При изучении функции одной переменной кроме производной первого порядка, характеризующей скорость изменения какого-либо процесса, мы ввели понятие второй производной, которая отвечала за ускорение. У функции двух переменных существует две частные производные, которые в общем случае также являются функциями тех же переменных, и, следовательно, их снова можно дифференцировать и по х, и по у. Покажем, как это делается.
17.2. Частные производные высших порядков
Пусть функция z = f(x,y) непрерывна вместе со своими частными производными  и
и  в некоторой области D плоскости ХОY.
в некоторой области D плоскости ХОY.
Определение 17.1. Частными производными второго порядка (или вторыми частными производными) называются производные от производных  и
и  .
.
Вторые частные производные обозначаются так:
 ,
,
здесь функция последовательно дифференцируется по х дважды;
 ,
,
здесь f дифференцируется сначала по х, а потом результат по у;
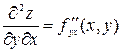 ,
,
здесь f дифференцируется сначала по у, а потом результат по х;
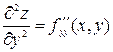 ,
,
здесь f дифференцируется дважды по у.
Первая и последняя производные называются иногда чистыми, а вторая и третья – смешанными производными второго порядка.
Можно доказать (см. учебник Кремера)), что
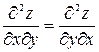 ,
,
при условии непрерывности этих производных в заданных точках, т. е. вторая смешанная производная не зависит от порядка дифференцирования и поэтому четыре частных производных сводятся к трем.
Производные второго порядка можно вновь дифференцировать как по х, так и по у. Получим производные третьего порядка, две из которых чистые, а остальные шесть – смешанные:
 ,
, 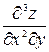 ,
, 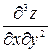 ,
,  .
.
Здесь мы учли, что
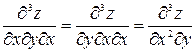 и
и 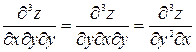 ,
,
и поэтому восемь частных производных сводятся к четырем.
Этот процесс можно продолжить и получить производные любого порядка, при условии, что все они непрерывны в заданной точке.
Пример 17.1. Вычислить производные второго порядка от функции 
Решение. Найдем производные первого порядка, учитывая, что частная производная по х вычисляется в предположении, что у – постоянная и наоборот:
 ,
, 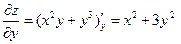 .
.
Найдем производные второго порядка:
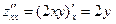 ,
, 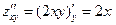 ,
, 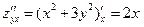 ,
,  .
.
Пример 17.2. Дана функция 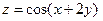 . Показать, что
. Показать, что  .
.
Решение. Найдем последовательно значения всех производных и проверим данное равенство.
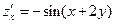 ,
,  ,
,  ,
,  .
.
Подставим найденные значения в исходное равенство:
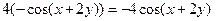 .
.
Мы видим, что равенство  для заданной функции выполняется.
для заданной функции выполняется.
Пример 17.3.Дана функция 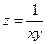 . Показать, что
. Показать, что  .
.
Решение.
 ,
, 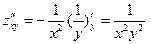 ,
, 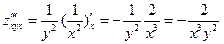
– это левая часть равенства.
Для вычисления правой учтем, что  уже известно, и найдем
уже известно, и найдем
 ,
,  .
.
Т.о. исходное равенство для заданной функции.
Как видно из приведенных примеров, следует соблюдать бдительность и отделять по возможности те переменные, которые в данном случае играют роль постоянной.
17.3. Экстремумы функции двух переменных
Мы достаточно подробно обсуждали экстремумы функции одной переменной. Перенесем эти знания на функции двух переменных.
Определение 17.2. Точка  называется точкой максимума функции
называется точкой максимума функции  , если
, если

для всех точек (х,у), достаточно близких к точке  и отличных от нее (рис. 17.1).
и отличных от нее (рис. 17.1).
Определение 17.2. Точка  называется точкой минимума функции
называется точкой минимума функции  , если
, если

для всех точек (х,у), достаточно близких к точке  и отличных от нее. (рис. 17.2).
и отличных от нее. (рис. 17.2).
Точки, в которых частные производные равны нулю или не существуют, называются критическими.
Иногда точку экстремума и ее характер можно определить из соображений здравого смысла.
Например, функция  имеет минимум при
имеет минимум при 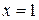 и
и  , т.е. в точке М(1,2). Действительно, для любых
, т.е. в точке М(1,2). Действительно, для любых  первое слагаемое будет расти, и для
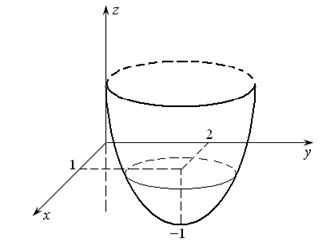
первое слагаемое будет расти, и для  – тоже, поэтому в точке М(1,2) функция имеет минимум, причем
– тоже, поэтому в точке М(1,2) функция имеет минимум, причем  (рис. 17.1).
(рис. 17.1).

– Конец работы –
Эта тема принадлежит разделу:
Лекция 13 ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Лекция ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ У Сойер английский математик и педагог... Рис... Как ведет себя функция в остальных точках мы не знаем поэтому торопиться с общим графиком не будем Мы исследуем ее...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. ЭКСТЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов