Ортогональный базис
Ортогональный базис
Материал из Википедии — свободной энциклопедии
Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты.
Содержание
- 1 Конечномерный случай
- 2 Бесконечномерный случай
- 3 Примеры
- 4 Литература
- 5 См. также
Конечномерный случай[править | править исходный текст]
Ортогональный базис — базис, составленный из попарно ортогональных векторов.
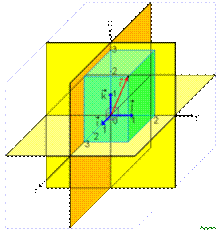

Ортонормированный базис в 3-мерном евклидовом пространстве
Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.
Последнее удобно записывается при помощи символа Кронекера:

то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают ( ), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.
), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.
Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности.
Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы).
Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.
Коэффициенты в разложении вектора по ортогональному базису:
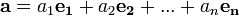
можно найти так:
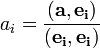 .
.
Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора 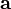 квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:
квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:
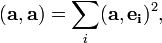
Аналогичные соотношения имеют место и для бесконечномерного случая (см. ниже).
Бесконечномерный случай[править | править исходный текст]
Ортогональный базис — система попарно ортогональных элементов  гильбертова пространства
гильбертова пространства  такая, что любой элемент
такая, что любой элемент  однозначно представим в виде сходящегося по норме ряда
однозначно представим в виде сходящегося по норме ряда

называемого рядом Фурье элемента  по системе
по системе  .
.
Часто базис  выбирается так, что
выбирается так, что  , и тогда он называется ортонормированным базисом. В этом случае числа
, и тогда он называется ортонормированным базисом. В этом случае числа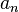 , называются коэффициентами Фурье элемента
, называются коэффициентами Фурье элемента 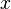 по ортонормированному базису
по ортонормированному базису  , имеют вид
, имеют вид
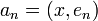 .
.
Необходимым и достаточным условием того, чтобы ортонормированная система  была базисом, является равенство Парсеваля.
была базисом, является равенство Парсеваля.
Гильбертово пространство, имеющее ортонормированный базис, является сепарабельным, и обратно, во всяком сепарабельном гильбертовом пространстве существует ортонормированный базис.
Если задана произвольная система чисел 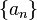 такая, что
такая, что 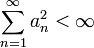 , то в случае гильбертова пространства с ортонормированным базисом
, то в случае гильбертова пространства с ортонормированным базисом  ряд
ряд 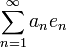 — сходится по норме к некоторому элементу
— сходится по норме к некоторому элементу  . Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству
. Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству  (теорема Рисса — Фишера).
(теорема Рисса — Фишера).
Примеры[править | править исходный текст]
- Стандартный базис
 в n-мерном евклидовом пространстве Rn является ортонормированным.
в n-мерном евклидовом пространстве Rn является ортонормированным.
- Множество
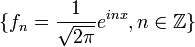 образует ортонормированый базис в L2([-π, π]).
образует ортонормированый базис в L2([-π, π]).
Автокорреляционная функция
График 100 случайных величин со скрытой синусоидой. Автокорреляционная функция позволяет увидеть периодичность в ряде…Содержание
- 1 Применение в технике
- 2 Другие применения
- 3 См. также
- 4 Ссылки
Применение в технике[править | править исходный текст]
Корреляционные свойства кодовых последовательностей, используемых в широкополосных системах, зависят от типа кодовой последовательности, её длины, частоты следования её символов и от её посимвольной структуры.
Изучение АКФ играет важную роль при выборе кодовых последовательностей с точки зрения наименьшей вероятности установления ложной синхронизации.
Интеграл
Определённый интеграл как площадь фигурыСодержание
- 1 Типы интегралов
- 1.1 По области интегрирования
- 2 Интегралы, зависящие от параметров
- 2.1 Дифференцирование по параметру
- 3 История
- 3.1 Интеграл в древности
- 3.2 Обозначение
- 4 См. также
- 5 Примечания
- 6 Литература
- 7 Ссылки
Типы интегралов[править | править исходный текст]
- Определённый интеграл и Неопределённый интеграл
- Интеграл Римана и Римана — Стилтьеса
- Интеграл Лебега и Лебега — Стилтьеса
- Интеграл Даниэля
По области интегрирования[править | править исходный текст]
- Кратный интеграл
- Криволинейный интеграл
- Поверхностный интеграл
Интегралы, зависящие от параметров[править | править исходный текст]
Основная статья: Зависящий от параметра интеграл
Дифференцирование по параметру[править | править исходный текст]
Пусть задан интеграл вида
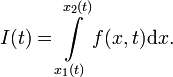
В таком случае, производная по параметру t будет равна[1]
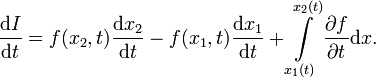
История[править | править исходный текст]
Интеграл в древности[править | править исходный текст]
Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 г. до н. э.[источник не указан 83 дня], Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н. э. Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод впоследствии использовали Цзу Чунчжи и Цзу Гэн для нахождения объёма шара.
Следующий крупный шаг в исчисление интегралов был сделан в Ираке, в XI веке, математиком Ибн ал-Хайсамом (известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвёртой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определённого интеграла, чтобы найти объём параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвёртой степени. Таким образом, он был близок к поиску общей формулы для интегралов от полиномов, но он не касается любых многочленов выше четвёртой степени.
Следующий значительный прогресс в исчислении интегралов появится лишь в XVI веке. В работах Кавальери с его методом неделимых, а также в работах Ферма, были заложены основы современного интегрального исчисления. Дальнейшие шаги были сделаны в начале XVII века Барроу и Торричелли, которые представили первые намеки на связь между интегрированием и дифференцированием.
Обозначение[править | править исходный текст]
Ньютон использовал (не везде) в качестве символа интегрирования значок квадрата (перед обозначением функции или вокруг него), но эти обозначения не получили широкого распространения. Современное обозначение неопределённого интеграла было введено Лейбницем в 1675 году. Он образовал интегральный символ  из буквы ſ («длинная s») — сокращения словалат. summa (тогда ſumma, сумма).[2] Современное обозначение определённого интеграла, с указанием пределов интегрирования, были впервые предложены Жаном Батистом Жозефом Фурье в 1819-20 годах.
из буквы ſ («длинная s») — сокращения словалат. summa (тогда ſumma, сумма).[2] Современное обозначение определённого интеграла, с указанием пределов интегрирования, были впервые предложены Жаном Батистом Жозефом Фурье в 1819-20 годах.
Скалярное произведение
Скаля́рное произведе́ние иногда внутреннее произведение — операция над двумя векторами, результатом которой является число (скаляр), не… Обычно используется одно из следующих обозначений: ,Содержание
[убрать]
- 1 Определение
- 2 Геометрическое определение
- 3 Связанные определения
- 4 Примеры
- 5 Свойства
- 5.1 Неравенство Коши — Буняковского
- 6 История
- 7 Вариации и обобщения
- 8 См. также
- 9 Примечания
- 10 Ссылки
Определение[править | править исходный текст]
Скалярным произведением в векторном пространстве  над полем
над полем 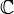 комплексных (или
комплексных (или 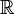 вещественных) чиселназывается функция
вещественных) чиселназывается функция 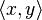 для элементов
для элементов  , принимающая значения в
, принимающая значения в  (или
(или  ), определенная для каждой пары элементов и удовлетворяющая следующим условиям:
), определенная для каждой пары элементов и удовлетворяющая следующим условиям:
- для любых трех элементов
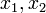 и
и 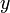 пространства
пространства  и любых чисел
и любых чисел 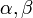 из
из 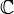 (или
(или  ) справедливо равенство
) справедливо равенство  (линейность скалярного произведения по первому аргументу);
(линейность скалярного произведения по первому аргументу); - для любых
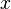 и
и 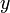 справедливо равенство
справедливо равенство 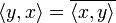 , где черта означает комплексное сопряжение (эрмитова симметричность);
, где черта означает комплексное сопряжение (эрмитова симметричность); - для любого
 имеем
имеем  , причем
, причем 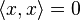 только при
только при 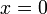 (положительная определенность скалярного произведения).
(положительная определенность скалярного произведения).
Заметим, что из п.2 определения следует, что 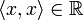 . Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения.
. Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения.
Геометрическое определение[править | править исходный текст]


A • B = |A| |B| cos(θ)
Если определения длины вектора и угла между векторами введены независимым образом до введения понятия скалярного произведения (как правило, так и поступают при изложении классической геометрии), то скалярное произведение определяется через длины сомножителей и угол между ними:
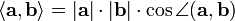
Современная аксиоматика обычно строится начиная со скалярного произведения, и тогда длина вектора и угол определяются уже через скалярное произведение (см. ниже).
Связанные определения[править | править исходный текст]
- Вещественное конечномерное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.
В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:
- Длина вектора, под которой обычно понимается его евклидова норма:
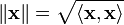 (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
(термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств). - Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число,косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):

- Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например,ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
- Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называетсяпредгильбертовым пространством.
- При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
- Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым(важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.
Примеры[править | править исходный текст]
- В трёхмерном вещественном векторном пространстве векторов
 введение скалярного произведения по формуле
введение скалярного произведения по формуле  превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).
превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства). - В любом евклидовом пространстве (размерности n) всегда можно выбрать[1] ортонормированный базис

при разложении векторов по которому:
 ,
,
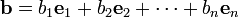 итд,
итд,
скалярное произведение будет выражаться приведённой следующей формулой:
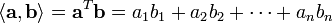 .
.
- В таком же, но комплексном, пространстве, скалярное произведение вводится по несколько другой формуле:
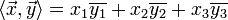 . Здесь через
. Здесь через 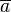 обозначено число, комплексно сопряжённое к
обозначено число, комплексно сопряжённое к  . При таком определении скалярное произведение становится положительно определённым. Без комплексного сопряжения аксиомаэрмитовости скалярного произведения была бы нарушена, а значит, вещественности определённой через него нормывектора добиться бы не удалось, то есть норма в обычном смысле им бы не порождалась.
. При таком определении скалярное произведение становится положительно определённым. Без комплексного сопряжения аксиомаэрмитовости скалярного произведения была бы нарушена, а значит, вещественности определённой через него нормывектора добиться бы не удалось, то есть норма в обычном смысле им бы не порождалась.
- В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных функций можно ввести положительно определённое скалярное произведение:
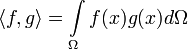
- В аналогичном случае для комплексных функций, если требуется эрмитовость (и положительная определённость) скалярного произведения, надо добавить комплексное сопряжение к f или g под интегралом.
- При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора
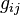 :
:

при этом сама метрика (говоря точнее, ее представление в данном базисе) так связана со скалярными произведениями базисных векторов 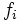 :
:
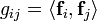
- (метрика в ортонормированных базисах тривиальна, то есть представлена единичной матрицей
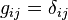 )
)
- Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:
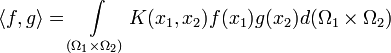

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).
Свойства[править | править исходный текст]
- теорема косинусов легко выводится с использованием скалярного произведения:
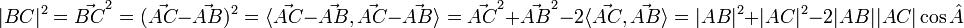
- Угол между векторами:
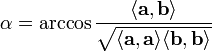
- Оценка угла между векторами:
в формуле 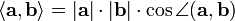 знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
- Проекция вектора
 на направление, определяемое единичным вектором
на направление, определяемое единичным вектором  :
:
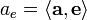 ,
,
- условие ортогональности[2] (перпендикулярности) векторов
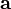 и
и 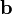 :
:

- Площадь параллелограмма, натянутого на два вектора
 и
и 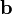 , равна
, равна

Неравенство Коши — Буняковского[править | править исходный текст]
Для любых элементов  и
и 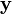 линейного пространства со скалярным произведением выполняется неравенство [1]
линейного пространства со скалярным произведением выполняется неравенство [1]

История[править | править исходный текст]
Скалярное произведение было введено У. Гамильтоном в 1846 году[3] одновременно с векторным произведением в связи скватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю[4].
Вариации и обобщения[править | править исходный текст]
Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам. Аналогичное обобщение в принципе нетрудно сделать и в бесконечномерном случае (Для бесконечномерных пространств функций — см. примеры (выше)).
См. также[править | править исходный текст]
- Псевдоскалярное произведение
- Внешнее произведение
- Векторное произведение
- Смешанное произведение
- Гильбертово пространство
- Метрический тензор
Примечания[править | править исходный текст]
- ↑ Ортонормированность базиса определяется условием
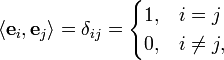
заключающемся в равенстве нулю скалярных произведений разных базисных векторов, например, первого и второго, первого и третьего, итд (ортогональность), и равенстве единице — скалярного произведения каждого базисного вектора с самим собой (нормированность). Упоминаемые в основном тексте формулы получаются прямым перемножением векторов, разложенных по такому базису, учитывая свойства скалярного произведения, особенно его билинейность, позволяющую раскрывать скобки итп как при вычислениях с обычными числами.
- ↑ В абстрактной формулировке названное условие
 — это всего лишь определение ортогональности. Аналогично, две формулы выше в абстрактной формулировке также являются просто определениями соответствующих понятий через скалярное произведение, но они все могут с успехом быть использованы в конкретных вычислениях, например, в элементарной геометрии, независимо от того, какая система определений используется, современная абстрактная или традиционная элементарная.
— это всего лишь определение ортогональности. Аналогично, две формулы выше в абстрактной формулировке также являются просто определениями соответствующих понятий через скалярное произведение, но они все могут с успехом быть использованы в конкретных вычислениях, например, в элементарной геометрии, независимо от того, какая система определений используется, современная абстрактная или традиционная элементарная. - ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Вектор (математика)
Материал из Википедии — свободной энциклопедии


Вектор 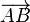
У этого термина существуют и другие значения, см. Вектор.
Ве́ктор — понятие, широко используемое в математике, изначально возникшее как геометрическая абстракция объектов, характеризуемых одновременно направлением и величиной (таких как скорость, момент силы) — направленный отрезок в евклидовом пространстве[⇨], обобщённое до представления в виде упорядоченной последовательности  компонент в
компонент в  -мерном пространстве[⇨] (и в развитие этой интерпретации используется в информатике для обозначения последовательности однородных элементов[⇨]) и до произвольного элемента алгебры, определённой над полем[⇨]. Во всех случаях вместе с вектором определяется сопутствующее понятие скаляра — объекта, характеризующегося только величиной (число, компонента
-мерном пространстве[⇨] (и в развитие этой интерпретации используется в информатике для обозначения последовательности однородных элементов[⇨]) и до произвольного элемента алгебры, определённой над полем[⇨]. Во всех случаях вместе с вектором определяется сопутствующее понятие скаляра — объекта, характеризующегося только величиной (число, компонента  -мерного пространства, элемент поля), определяются операции умножения вектора на скаляр, скалярного произведения двух векторов (комбинации векторов, дающей в результате скаляр)[⇨].
-мерного пространства, элемент поля), определяются операции умножения вектора на скаляр, скалярного произведения двух векторов (комбинации векторов, дающей в результате скаляр)[⇨].
Является одним из основополагающих понятий линейной алгебры. При использовании наиболее общего определения векторами оказываются практически все изучаемые в линейной алгебре объекты, в том числе матрицы, тензоры, однако, при наличии в окружающем контексте этих объектов, под вектором понимаются соответственно вектор-строка или вектор-столбец, тензор первого ранга. Свойства операций над векторами изучаются в векторном исчислении.
В геометрических интерпретациях векторы обозначаются буквами с чертой или стрелкой сверху (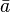 ,
,  ) или обозначением точек, объединёнными стрелкой сверху (
) или обозначением точек, объединёнными стрелкой сверху ( ), в алгебраических интерпретациях — прямым жирным шрифтом (
), в алгебраических интерпретациях — прямым жирным шрифтом ( ), встречаются и другие обозначения[⇨].
), встречаются и другие обозначения[⇨].
Содержание
[убрать]
- 1 Общее определение
- 2 В евклидовом пространстве
- 3 Вектор в линейном пространстве
- 3.1 Операции над векторами
- 3.2 Евклидовы и нормированные пространства
- 4 Геометрическая интерпретация
- 4.1 Свободные, скользящие и фиксированные векторы
- 4.2 Операции над векторами
- 4.2.1 Сложение
- 4.2.2 Вычитание
- 4.2.3 Скалярное произведение
- 4.2.4 Векторное произведение
- 4.2.5 Смешанное произведение
- 4.2.6 Базис и разложение по базису
- 4.3 Обозначения
- 5 Физическая интерпретация
- 6 Вектор как последовательность
- 7 История
- 8 См. также
- 9 Литература
- 10 Ссылки
Общее определение[править | править исходный текст]
Наиболее общее определение вектора даётся средствами общей алгебры. Пусть 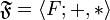 — некоторое поле с аддитивной операцией
— некоторое поле с аддитивной операцией  , мультипликативной операцией
, мультипликативной операцией  , аддитивной единицей
, аддитивной единицей 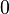 и мультипликативной единицей
и мультипликативной единицей  . Пусть
. Пусть  — некоторая абелева группа с единицей
— некоторая абелева группа с единицей  . Если существует операция
. Если существует операция  , такая что для любых
, такая что для любых 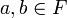 и для любых
и для любых 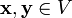 выполняются соотношения:
выполняются соотношения:
 ,
,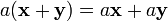 ,
, ,
, ,
,
тогда 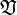 называется векторным пространством над полем
называется векторным пространством над полем 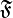 (или линейным пространством), элементы
(или линейным пространством), элементы  называютсявекторами, элементы
называютсявекторами, элементы 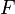 — скалярами, а указанная операция
— скалярами, а указанная операция  — умножением вектора на скаляр.
— умножением вектора на скаляр.
Многие результаты линейной алгебры обобщены до унитарных модулей над некоммутативными телами и даже произвольныхмодулей над кольцами, таким образом, в наиболее общем случае, в некоторых контекстах, вектором может быть назван как любой элемент модуля над кольцом.
В евклидовом пространстве[править | править исходный текст]
Вектор в арифметическом  -мерном пространстве является частным случаем определения вектора в абстрактной алгебре: если
-мерном пространстве является частным случаем определения вектора в абстрактной алгебре: если
- в качестве поля
 взять поле вещественных чисел
взять поле вещественных чисел 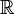 с их обычными операциями сложения и умножения;
с их обычными операциями сложения и умножения; - n-мерное пространство
 задать как декартову степень множества вещественных чисел
задать как декартову степень множества вещественных чисел 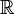 ;
; - точку — как кортеж
 длины n из вещественных чисел, что соответствует определению пространства как множества точек;
длины n из вещественных чисел, что соответствует определению пространства как множества точек; - операцию «+» для
 задать следующим образом:
задать следующим образом: 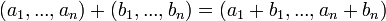 ,
, - нейтральный элемент:
 =(0,…,0),
=(0,…,0), - обратный элемент:
 ;
; - операцию умножения на скаляр задать выражением
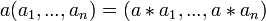
— тогда алгебраический вектор, задаваемый кортежем длиной n, состоящим из вещественных чисел, является
арифметическим вектором векторного пространства 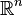 над полем вещественных чисел
над полем вещественных чисел 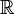 .
.
Вектор в планарной евклидовой геометрии (связанный вектор) — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора.
Два вектора равны, если разности по каждой из координат с одинаковыми номерами конечной и начальной точки для этих векторов равны. Эти разности называются пространственными координатами вектора.
Свободный вектор задается классом всех равных связанных векторов и полагается равным каждому из этих связанных векторов и таким образом может быть определен как вектор в арифметическом пространстве (кортеж чисел длины n (пространственных координат равных ему связанных векторов) с операциями сложения и умножения на скаляр).
Результатом операций со связанными векторами принимается вектор, начальная точка которого совпадает с начальной точкой первого слагаемого при сложении векторов и начальной точке исходного вектора при умножении вектора на скаляр.
Нуль-вектор — вектор, начало и конец которого совпадают.
Также существует более распространенное определение вектора как направленного отрезка, но оно требует определения прямой и отрезка в n-мерном пространстве. Однако, прямую и отрезок можно задать через вектор, определённый алгебраически:
- Прямая, на которой лежит ненулевой вектор
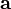 с началом в точке
с началом в точке 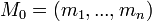 , заданный свободным вектором с пространственными координатами
, заданный свободным вектором с пространственными координатами  — множество точек
— множество точек 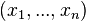 , удовлетворяющее условию
, удовлетворяющее условию 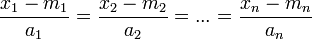
- Отрезок MN — множество всех точек O (удовлетворяющих условию
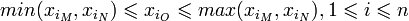 ), все различные точки которого принадлежат одной прямой. Точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
), все различные точки которого принадлежат одной прямой. Точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
При введении операций получения скалярного произведения двух векторов, угла между векторами и длины вектора, как расстояния между начальной и конечной точками вектора (см. ниже), векторное пространство 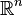 становится евклидовым нормированным пространством и
становится евклидовым нормированным пространством и
- при n=3 соответствует модели физического трехмерного пространства;
- при n=2 — плоскости этого пространства;
- при n=1 точка соответствует числу на числовой прямой, свободный вектор — разности двух чисел, а длина вектора соответствует модулю;
- при n=0 существует только одна точка (задается пустым кортежем), декартово произведение содержит только пустой кортеж, соответственно пространство представляет собой точку, есть только нулевой вектор;
- пространство при n>3 не имеет наглядной геометрической интерпретации, так как физическое пространство трёхмерно.
Скалярное произведение в этом случае определяется по формуле: 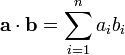 , где
, где 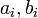 — пространственные координаты векторов
— пространственные координаты векторов 
Длина вектора 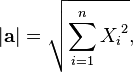 где
где  — пространственные координаты вектора.
— пространственные координаты вектора.
Угол между двумя векторами  определяется через скалярное произведение
определяется через скалярное произведение  где
где 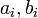 — пространственные координаты векторов
— пространственные координаты векторов  .
.
Вектор в линейном пространстве[править | править исходный текст]
Линейное пространство — это множество элементов, называемых векторами, над которыми определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых базисом линейного пространства. Количество векторов в базисе равно размерности пространства. Любой вектор из пространства можно представить, как линейную комбинацию базисных векторов. То есть, если у нас есть базис  , то
, то  , где
, где  — это поле, над которым определенно линейное пространство
— это поле, над которым определенно линейное пространство  .
.
Выбор базиса в линейном пространстве неоднозначен, однако коэффициенты векторов при измерении базиса связанны определённым образом. Пусть есть базис 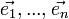 и
и 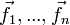 . Причём:
. Причём:  . Матрица
. Матрица  , полученная из коэффициентов
, полученная из коэффициентов  называться матрицей перехода от базиса
называться матрицей перехода от базиса  к базису
к базису 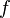 и связывает координаты вектора в различных базисах следующем образом:
и связывает координаты вектора в различных базисах следующем образом: 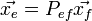 . Связь между матрицами перехода между двумя базисами:
. Связь между матрицами перехода между двумя базисами: 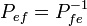 . Векторы могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
. Векторы могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
Операции над векторами[править | править исходный текст]
Пусть в линейном пространстве выбран базис  и в нём представлены вектора
и в нём представлены вектора  ,
, 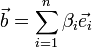 , тогда суммой векторов
, тогда суммой векторов 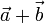 будет называется следующий вектор:
будет называется следующий вектор: 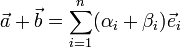 .
.
Пусть есть число  , тогда произведением вектора
, тогда произведением вектора  на число
на число  будет называться следующий вектор:
будет называться следующий вектор: 
Два ненулевых вектора  и
и 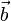 называются коллинеарными, если
называются коллинеарными, если 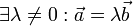 .
.
Евклидовы и нормированные пространства[править | править исходный текст]
Основная статья: Евклидово пространство
Основная статья: Нормированное пространство
Функция  (в другом обозначении
(в другом обозначении 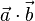 ), ставящая любым двум векторам
), ставящая любым двум векторам 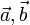 в соответствие число и удовлетворяющая следующим аксиомам:
в соответствие число и удовлетворяющая следующим аксиомам:
- Линейность по первому аргументу:
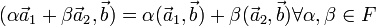
- Эрмитова симметричность:
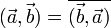 (в случае если векторы определены над полем действительных чисел, то
(в случае если векторы определены над полем действительных чисел, то  )
) - Положительная определённость:
 тогда и только тогда, когда
тогда и только тогда, когда  ,
,
называется скалярным произведением вектора  на вектор
на вектор 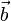 . Конечномерное линейное пространство с введённым скалярным произведением называется евклидовым. Для пространств над полем комплексных чисел иногда применяют термин унитарное пространство.
. Конечномерное линейное пространство с введённым скалярным произведением называется евклидовым. Для пространств над полем комплексных чисел иногда применяют термин унитарное пространство.
Два ненулевых вектора 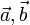 называются ортогональными, если
называются ортогональными, если 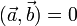 .
.
Базис  евклидова пространства называется ортогональным, если
евклидова пространства называется ортогональным, если 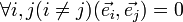 . Базис называется ортонормированным, если
. Базис называется ортонормированным, если  , где
, где  — символ Кронекера.
— символ Кронекера.
Скалярное произведение является билинейной формой, поэтому его можно записать в следующем виде:
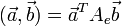 , где
, где  — матрица Грамма.
— матрица Грамма.
В случае ортонормированного базиса матрица будет единичной, и тогда, если  ,
, 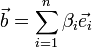 , то
, то
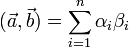 в случае действительного пространства и
в случае действительного пространства и  в случае комплексного.
в случае комплексного.
Так же в линейном пространстве можно ввести понятие нормы. Это функция, ставящая в соответствие любому вектору линейного пространства неотрицательное вещественное число и удовлетворяющая следующим аксиомам:
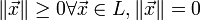 тогда и только тогда, когда
тогда и только тогда, когда 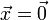 .
.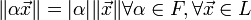 .
.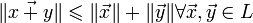 .
.
Угол 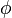 между векторами
между векторами 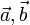 определяется, как
определяется, как 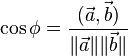 .
.
Геометрическая интерпретация[править | править исходный текст]
Вектор в геометрии — упорядоченная пара точек (или направленный отрезок), одна из которых называется началом, вторая — концом вектора. Операция сложения вводится по правилу треугольника: пусть есть векторы  и
и  . Оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
. Оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
Операция умножения вектора на число вводится следующим образом: пусть есть вектор  и число
и число  , тогда вектор
, тогда вектор 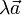 получается изменением длины вектора
получается изменением длины вектора  в
в  раз. Направление вектора сохраняется, если
раз. Направление вектора сохраняется, если 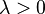 и меняется, если
и меняется, если  .
.
Нулевой вектор — такой, начало которого совпадает с его концом.
Противоположным данному называется вектор, начало которого совпадает с концом данного, а конец с началом данного (то есть такой, сумма которого с данным дает нулевой вектор).
Два геометрических вектора называются ортогональными, если они (как направленные отрезки) перпендикулярны друг другу.
Норма геометрического вектора определяется как длина соответвующего ему отрезка. Чаще всего называется модулем вектора и обозначается как  .
.
Свободные, скользящие и фиксированные векторы[править | править исходный текст]
Иногда вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или — одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Иными словами, подразумевается, что свободный вектор может быть перенесен (параллельным переносом) как угодно (так, чтобы его начало совпало с любой точкой пространства), однако не перестает от этого быть собой. Скользящий же вектор может так же свободно переноситься только вдоль прямой, на которой он лежит, а фиксированный вообще не может переноситься. То есть его приложение к другой точке не имеет смысла; в частности любые операции, такие как сложение или вычитание, фиксированного вектора с фиксированным вектором, имеющим другое начало («приложенным к другой точке») не определены (не имеют смысла).
- Важно заметить, что все операции над векторами (сложение, умножение на число, скалярное и векторное произведения, вычисление модуля или длины, угла между векторами итд) в принципе определены одинаково для всех типов векторов (свободных, скользящих или фиксированных), различие в типах сводится в этом отношении только к тому, что для скользящих и фиксированных наложено ограничение на возможность осуществления операций между двумя векторами, имеющими разное начало (так, для двух фиксированных векторов запрещено — или лишено смысла — сложение, если их начала отличаются; однако для всех случаев, когда эта операция разрешена — или имеет смысл — она такова же, как для свободных векторов). Поэтому часто тип вектора вообще явно не указывается, подразумевается, что он очевиден из контекста. Более того, один и тот же вектор в зависимости от контекста задачи может рассматриваться как фиксированный, скользящий или свободный, например, в механике векторы сил, приложенных к телу, могут суммироваться независимо от точки приложения при нахождении равнодействующей (и в статике, и в динамике при исследовании движения центра масс, изменения импульса итп), но не могут складываться друг с другом без учета точек приложения при вычислении вращающего момента (также и в статике и в динамике).
Можно дать такие строгие определения:
Говорят, что свободные векторы 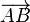 и
и 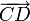 равны, если найдутся точки
равны, если найдутся точки  и
и 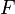 такие, что четырёхугольники
такие, что четырёхугольники 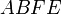 и
и  — параллелограммы.
— параллелограммы.
- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки
 располагаются на одной прямой. В противном случае определение выглядит проще:
располагаются на одной прямой. В противном случае определение выглядит проще:
Говорят, что свободные векторы 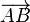 и
и 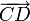 , не лежащие на одной прямой, равны, если четырёхугольник
, не лежащие на одной прямой, равны, если четырёхугольник  —параллелограмм.
—параллелограмм.
Говорят, что скользящие векторы 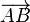 и
и 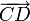 равны, если
равны, если
- точки
 располагаются на одной прямой,
располагаются на одной прямой, - векторы
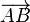 и
и 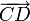 равны между собой как свободные векторы.
равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике —сила. Перенос такого начала вектора вдоль прямой, на которой он лежит, не меняет момента силы ни относительно никакой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Говорят, что фиксированные векторы  и
и  равны, если попарно совпадают точки
равны, если попарно совпадают точки  и
и  ,
,  и
и  .
.
Вектором в одном случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Операции над векторами[править | править исходный текст]
Сложение[править | править исходный текст]
Операцию сложения геометрических векторов можно определить несколькими в принципе эквивалентными способами, каждый из которых однако может быть удобнее или естественнее в зависимости от ситуации и типа рассматриваемых векторов. Так, правило треугольника наиболее простое и геометрически фундаментальное, удобно для сложения любого количества векторов, однако правило параллелограмма более удобно для фиксированных или скользящих векторов, так как не требует переноса второго слагаемого (что в принципе могло бы смущать или запутывать в этих случаях) для построения суммы, то есть удобно для сложения векторов с началом в одной точке, вдобавок имея то преимущество, что в нём более очевидно равноправие слагаемых; координатное же определение, являясь простым и удобным, бывает очень полезно для вычислений.
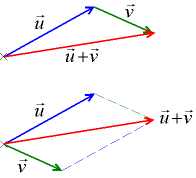
Два вектора u, v и вектор их суммы
Правило треугольника. Для сложения двух векторов  и
и  по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего — с концом второго и т. д., сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).
по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего — с концом второго и т. д., сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).
Правило параллелограмма. Для сложения двух векторов  и
и  по правилупараллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
по правилупараллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Сложение векторов с использованием координат. Каждая координата (см. Базис и разложение по базису) суммы векторов есть сумма соответствующей координаты всех (двух или более) суммируемых векторов. Например, для двумерного случая:

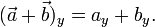
(Могут быть использованы прямоугольные или косоугольные координаты; правило сложения остаются одинаковыми для обоих этих типов координат).
- Модуль (длину) вектора суммы
 можно вычислить, например, используя теорему косинусов
можно вычислить, например, используя теорему косинусов  где
где  — угол между отрезками, изображающими данные векторы, когда начало одного вектора совпадает с концом другого. Или:
— угол между отрезками, изображающими данные векторы, когда начало одного вектора совпадает с концом другого. Или:  где
где  — угол между векторами (выходящими из одной точки).
— угол между векторами (выходящими из одной точки).
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Прямые, на которых расположены векторы и , пересекаются всегда, за… Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во…Корреляция. Автокорреляция
Взаимная корреляция
Рассмотрим две последовательности данных, представляющие собой выборки двух сигналов, взятых с одинаковой частотой оцифровки, размерностью N – s1(k)… (1) Сумма произведений выборок случайных процессов стремится к исчезающее малому значению с увеличением N. Это объясняется…Автокорреляция
(3) Для вычисления одного элемента функции автокорреляции с индексом n находят… Пример. Пусть имеется процесс с периодическим повторением пятиразрядной последовательности Баркера +1 +1 +1 −1…Приложения корреляции
Корреляция и автокорреляция являются одним из «китов» цифровой обработки сигналов наравне со сверткой и преобразованием Фурье. Корреляция применяется в радарных и гидроакустических установках для дальнометрии и пеленгации (местоопределении), в которых сравниваются переданные и отраженные сигналы и по задержке определяются расстояние и местоположение, при детектировании сигналов в шуме, для синхронизации принимаемых данных (нахождении и детектировании начала посылки), в экономике, социологии, политологии для установления причинно-следственных связей. Функция автокорреляции применяется для оценки периодичности процессов, для выбора кодовых последовательностей для систем с шумоподобными сигналами (ШПС, примером может служить оценка уникальных кодов Баркера, рассмотренных выше).
_____________________________________________________________________________________