рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Уточнение понятия алгоритма
Реферат Курсовая Конспект
Уточнение понятия алгоритма
Уточнение понятия алгоритма - раздел Образование, АКСИОМАТИЧЕСКИАЯ ТЕОРИЯ «То, Что Вообще Может Быть Сказано, Может Быть Сказано Ясно, А О Чем Невоз...
«То, что вообще может быть сказано, может быть сказано ясно, а о чем невозможно говорить - о том следует молчать».
Людвиг Витгенштейн (Эпиграф, предпосланный изложению языка программирования АЛГОЛ-60.)
Точное математическое определение понятия «алгоритм» было выработано лишь в тридцатых годах XX века. Почему же до этого времени математики довольствовались интуитивным понятием алгоритма? Это связано с тем, что обычно понятие алгоритма встречалось в связи с конкретным решением задачи. Об алгоритме говорили лишь тогда, когда предлагался способ решения какого-либо класса задач. В начале XX века в математике накопилось большое количество задач, которые не поддавались решению, несмотря на то, что над ними думали первоклассные ученые. Возникло подозрение, что для некоторых из этих задач вообще не существует разрешающего алгоритма. Утверждение о неразрешимости того или иного класса задач можно было вывести, только имея точное определение алгоритма, надо было знать, несуществование чего требуется доказать.
Попытки дать строгое математическое определение алгоритма, согласующееся с интуитивным представлением об алгоритме, привели к выработке сразу нескольких определений (Черч, Пост, Тьюринг, Марков и др.). Впоследствии выяснилось, что все эти определения равносильны между собой и, следовательно, определяют одно и то же понятие.
В качестве основы для уточнения понятия алгоритма мы выбираем так называемые машины с неограниченными регистрами, или, короче, МНР [4]. Изложение на базе МНР привлекательно ввиду близости этих машин к реальным ЭВМ.
Каждый алгоритм имеет дело с данными - входными, промежуточными и выходными. Поскольку мы собираемся уточнять понятие алгоритма, нужно уточнить и понятие данных. В качестве данных для МНР мы ограничиваемся множеством Z0 неотрицательных целых чисел. Такое ограничение не является существенным, поскольку другие виды объектов и операции над ними могут быть закодированы натуральными числами и представлены как операции над натуральными числами.
Ниже мы перечислим все команды из списка предписаний МНР (для уточнения свойства «понятность»), однозначно определим действие каждой команды (для уточнения свойства «определенность») и опишем механизм реализации алгоритма (для уточнения свойства «точность»).
Машина с неограниченными регистрами является исполнителем, представляющим собой простой «идеализированный компьютер». Идеализация состоит в том, что каждый отдельный реальный компьютер ограничен как величиной чисел, которые поступают на вход, так и размером памяти (необходимой для запоминания промежуточных результатов), МНР лишена этих ограничений. Машина с неограниченными регистрами имеет неограниченно большую память, ячейки которой будем называть регистрами и обозначать  Каждый регистр в любой момент времени содержит неотрицательное целое число.
Каждый регистр в любой момент времени содержит неотрицательное целое число.
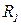
| 
| 
| 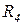
| ... |
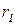
| 
| 
| 
| ... |
Рис. 3.1. Регистры МНР
При этом только конечное множество регистров содержит числа, отличные от нуля. Все остальные регистры заполнены нулями. Это допущение предполагает, что каждый алгоритм использует только конечный объем памяти.
В список предписаний МНР входит четыре команды: команда обнуления Z(n); команда прибавления единицы S(n); команда переадресации T(m, n) и команда условного переходам J(m, n, q). Команды обнуления, прибавления единицы и переадресации называются арифметическими.
| Обозначение команды | Действие, производимое МНР по данной команде |
| Z(n) | 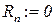
|
| S(n) | 
|
| T(m, n) | 
|
| J(m, n, q) | Если  , то перейти к вычислению команды алгоритма с номером q. , то перейти к вычислению команды алгоритма с номером q.
|
Рис. 3.2. Список предписаний МНР
Алгоритмом называется конечная непустая последовательность команд из списка предписаний МНР, начинающаяся с команды с номером 1.
Производя вычисления по данному алгоритму, МНР изменяет содержимое регистров памяти в точном соответствии с командами алгоритма. Исходное состояние памяти, то есть последовательность чисел  в регистрах
в регистрах  перед началом вычислений, называется начальной конфигурацией.
перед началом вычислений, называется начальной конфигурацией.
Предположим, что некоторый алгоритм P состоит из последовательности команд I1, I2, ..., Is. МНР начинает вычисление с команды I1, затем выполняются команды I2, I3 и т. д. до тех пор, пока не встретится команда вида J(m, n, q). В этом случае МНР переходит к выполнению команды, предписанной J(m, n, q) и текущим содержанием регистров Rm и Rn
Пример 3.2. Рассмотрим алгоритм P1
| I1 | J(1, 2, 6) |
| I2 | S(2) |
| I3 | S(3) |
| I4 | J(1, 2, 6) |
| I5 | J(1, 1, 2) |
| I6 | T(3, 1) |
Применим алгоритм к следующей начальной конфигурации:
| R1 | R2 | R3 | R4 | R5 | ... |
| 5 | 3 | 0 | 0 | 0 | ... |
Рис. 3.3. Начальная конфигурация
Ход вычисления на МНР по алгоритму P1 с начальной конфигурацией, изображенной на рисунке 3.3, можно представить, записывая последовательно сверху вниз конфигурации машины вместе со следующей командой, к которой она переходит на данном шаге.
| R1 | R2 | R3 | R4 | R5 | ... | Следующая команда | ||
| 5 | 3 | 0 | 0 | 0 | ... | I1 | ||
| 5 | 3 | 0 | 0 | 0 | ... | I2 | (так как R1 ¹ R2) | |
| 5 | 4 | 0 | 0 | 0 | ... | I3 | ||
| 5 | 4 | 1 | 0 | 0 | ... | I4 | ||
| 5 | 4 | 1 | 0 | 0 | ... | I5 | (так как R1 ¹ R2) | |
| 5 | 4 | 1 | 0 | 0 | ... | I2 | (так как R1 = R2) | |
| 5 | 5 | 1 | 0 | 0 | ... | I3 | ||
| 5 | 5 | 2 | 0 | 0 | ... | I4 | ||
| 5 | 5 | 2 | 0 | 0 | ... | I6 | (так как R1 = R2) | |
| 2 | 5 | 2 | 0 | 0 | ... | I7 |
Рис. 3.4. Вычисление по алгоритму P1
МНР выполняет алгоритм P: I1, I2, ..., Is до тех пор, пока это возможно. Вычисление останавливается тогда и только тогда, когда нет следующей команды, то есть когда МНР только что выполнила команду Ik и следующая команда в вычислении есть Iv, где v > s. Это может произойти одним из способов:
I) если Ik = Is (выполнена последняя команда в P) и Ik - арифметическая команда;
2) если Ik = J(m, n, q), Rm = Rn и q > s.
3) если Ik = J(m, n, q), Rm ¹ Rn и q = s.
В этом случае будем говорить, что вычисление остановилось после выполнения команды Ik, и заключительная конфигурации есть последовательность r1, r2, r3, ... содержимого регистров на этом шаге.
Результатом применения алгоритма к некоторой начальной конфигурации будем считать число r1 из регистра R1 заключительной конфигурации.
Бывают, конечно, вычисления, которые никогда не заканчиваются, например, никогда не заканчивается ни при какой начальной конфигурации вычисление по алгоритму:
| I1 | S(1) |
| I2 | J(1, 1, 1) |
В случае, если вычислительный процесс не заканчивается получением результата, говорят, что алгоритм неприменим к начальной конфигурации.
– Конец работы –
Эта тема принадлежит разделу:
АКСИОМАТИЧЕСКИАЯ ТЕОРИЯ
Е П Емельченков В Е Емельченков...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Уточнение понятия алгоритма
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов