Упражнения

5.1. Докажите непротиворечивость аксиоматической теории порядка – теории с одним бинарным отношением a, удовлетворяющим аксиомам транзитивности и антисимметричности.

5.2. Докажите непротиворечивость аксиоматической теории с одним бинарным отношением a, удовлетворяющим аксиомам симметричности и антисимметричности.

5.3. Докажите непротиворечивость аксиоматической теории строгого линейного порядка – теории с одним бинарным отношением a, удовлетворяющим аксиомам транзитивности, антисимметричности, антирефлексивности и связности.

5.4^*. Докажите непротиворечивость аксиоматической теории проективных плоскостей. Эта теория имеет дело с двумя типами объектов - прямыми и точками. Объекты связаны единственным отношением I инцидентности точки A и прямой a (обозначение: A I a). Все свойства прямых, точек и отношения инцидентности описываются тремя аксиомами:

D1. Существуют три точки не инцидентные одной прямой.

D2. Любые две различные точки инцидентны точно одной прямой.

D3. Любым двум различным прямым инцидентна точно одна точка.

Обсудим теперь свойство полноты аксиоматических теорий. Можно сказать, что аксиоматическая теория называется полной, если она содержит достаточное для какой-нибудь цели количество теорем. В зависимости от целей различают несколько видов полноты. Мы ограничимся рассмотрением лишь одного из них.

Определение 5.2. Аксиоматическая теория называется полной, если для любого утверждения A, сформулированного в терминах этой теории, по крайней мере, одно из утверждений A или доказуемо в этой теории.

Другими словами, аксиоматическая теория T является полной, если средств теории T достаточно для того, чтобы доказать или опровергнуть любое утверждение, сформулированное в терминах данной теории.

Теория, являющаяся одновременно непротиворечивой и полной, является максимальной в отношении непротиворечивости – в том смысле, что добавление к такой теории T в качестве аксиомы любого сформулированного в терминах этой теории предложения, не являющегося теоремой в T, приводит к противоречивой теории. Действительно, если T - непротиворечивая и полная теория и A - недоказуемое в T предложение, то после присоединения к T предложения A получаем новую теорию T1, в которой предложение A уже является теоремой. С другой стороны, в силу полноты теории T из недоказуемости предложения A следует доказуемость 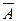. Таким образом, в теории T1 доказуемы предложения A и , и, следовательно, теория T1 противоречива.

Исследование аксиоматической теории на полноту является непростой задачей. Однако, иногда удается доказать неполноту теории, указав конкретное предложение, недоказуемое и неопровержимое в этой теории (предложение A теории T называется неопровержимым, если в T нельзя доказать предложение ).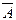

Докажем, например, неполноту аксиоматической теории эквивалентности T. Рассмотрим предложение A, утверждающее связность отношения a. На рисунке 5.2 с помощью двух графов заданы две модели теории эквивалентности.

Рис. 5.2. Две модели теории эквивалентности

В первой модели предложение A выполняется. Следовательно, в теории T невозможно доказать предложение . Действительно, если бы в T предложение было доказуемо, то это предложение должно было бы выполняться для всех интерпретаций T, в которых выполняются аксиомы теории, т. е. для всех моделей теории T. Так как в модели M1 предложение не выполняется, то в T невозможно доказать . Таким образом, A неопровержимо в T.

Во второй модели предложение A не выполняется. Поэтому в теории T предложение A недоказуемо.

Итак, мы указали конкретное предложение A теории T, которое недоказуемо и неопровержимо в T. Следовательно, теория T неполна.

Аналогично доказывается неполнота теории аффинных плоскостей. Рассмотрим, например, следующее предложение теории.

Предложение A. Пусть A, B, C – три точки плоскости не инцидентные одной прямой. Через D обозначим точку пересечения прямых l и m, проходящих через точки A и C соответственно, и таких, что m BA и l BC (рис. 5.3). Тогда прямые AC и BC пересекаются в единственной точке.

Рис. 5.3. Предложение A о пересечении прямых

Выше мы рассмотрели две модели теории аффинных плоскостей: обычную евклидову плоскость и конечную четырехточечную аффинную плоскость (рис. 4.1). Из первой модели следует неопровержимость предложение A, а из второй – его недоказуемость. Следовательно, теория аффинных плоскостей неполна.

Заканчивая обсуждение свойства полноты аксиоматических теорий, заметим, что многие современные аксиоматические теории неполны.