рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Формулировка аксиоматической теории
Реферат Курсовая Конспект
Формулировка аксиоматической теории
Формулировка аксиоматической теории - раздел Образование, АКСИОМАТИЧЕСКИАЯ ТЕОРИЯ В Этом Параграфе Вводится Понятия Формулировки Теории И Независимости Системы...
В этом параграфе вводится понятия формулировки теории и независимости системы аксиом.
Как уже говорилось, неформальная теория T включает в себя некоторый список T0 неопределяемых терминов, список T1 определяемых терминов, список P0 аксиом и список P1 всех остальных высказываний, которые можно вывести из P0 по некоторым фиксированным логическим правилам. Назначение множества T0 состоит в том, чтобы получить из него множество T0 È T1 всех используемых в теории T терминов; аналогично, множество P0 нужно для получения множества P0 È P1 всех теорем теории T. Упорядоченную пару <T0, P0 > обычно называют формулировкой теории T.
Изучение теории T может привести нас к обнаружению самых разнообразных и полезных других ее формулировок. Задание какой-либо из этих формулировок равносильно заданию некоторого подмножества  множества T0 È T1 и подмножества
множества T0 È T1 и подмножества  множества P0 È P1, состоящего из высказываний, выразимых в терминах элементов множества
множества P0 È P1, состоящего из высказываний, выразимых в терминах элементов множества  , причем из высказываний, входящих в
, причем из высказываний, входящих в  , можно вывести все остальные теоремы данной теории. Чтобы пара вида < T0, P0> была формулировкой теории T, достаточно, очевидно, чтобы термины из T0 могли быть определены через термины из
, можно вывести все остальные теоремы данной теории. Чтобы пара вида < T0, P0> была формулировкой теории T, достаточно, очевидно, чтобы термины из T0 могли быть определены через термины из  и чтобы высказывания из P0 могли быть выведены из высказываний из
и чтобы высказывания из P0 могли быть выведены из высказываний из  .
.
Для многих общеизвестных аксиоматических теорий имеются различные формулировки. Различные формулировки какой-либо теории - это ни что иное, как различные возможные подходы к одной и той же математической структуре. В зависимости от принятых критериев можно предпочесть ту или иную из таких различных формулировок. Основаниями для такого предпочтения могут, например, служить соображения эстетического характера; важную роль может здесь играть и желание иметь как можно более простое множество аксиом, а также возможность более изящных доказательств теорем. Одни исследователи предпочитают какую-либо конкретную формулировку теории, находя ее более «естественной», нежели остальные. Другие стремятся располагать формулировкой, включающей минимальное количество первичных терминов или аксиом.
Казалось бы, от формулировки аксиоматической теории ничего не зависит. Две разные формулировки <T0, P0 > и < ,
,  > одной теории T определяют, очевидно, одно и то же множество теорем. Однако, исследователи, отправляясь от разных формулировок, часто развивают теорию в различных направлениях. При этом множество теорем, доказанных исследователями, взявшими за основу формулировку <T0, P0 >, может значительно отличаться от множества теорем, доказанных исследователями, взявшими за основу формулировку <
> одной теории T определяют, очевидно, одно и то же множество теорем. Однако, исследователи, отправляясь от разных формулировок, часто развивают теорию в различных направлениях. При этом множество теорем, доказанных исследователями, взявшими за основу формулировку <T0, P0 >, может значительно отличаться от множества теорем, доказанных исследователями, взявшими за основу формулировку < ,
,  >. Различные формулировки теории во многих случаях определяют различные направления исследований. Так, например, теория графов и теория бинарных отношений значительно отличаются друг от друга наборами доказанных теорем, хотя по существу они являются различными формулировками одной и той же теории.
>. Различные формулировки теории во многих случаях определяют различные направления исследований. Так, например, теория графов и теория бинарных отношений значительно отличаются друг от друга наборами доказанных теорем, хотя по существу они являются различными формулировками одной и той же теории.
Формулировки неформальной теории можно характеризовать с помощью такого понятия, как независимость множества аксиом.
Определение 6.1. Множество аксиом называется независимым, если исключение любой аксиомы из этого множества приводит к уменьшению запаса теорем; в противном случае множество аксиом называют зависимым.
Отдельная аксиома (рассматриваемая как элемент множества аксиом некоторой формулировки) независима, если ее исключение из этого множества уменьшает запас теорем, и зависима в противном случае. Ясно, что независимая аксиома не может быть выведена из остальных аксиом. Разумеется, независимость какого-либо множества аксиом равносильна тому, что независима каждая аксиома из этого множества.
Рассмотрим непротиворечивую теорию T с формулировкой <T0, P0 >, и пусть A – одна из ее аксиом. Чтобы убедиться в независимости аксиомы A от остальных аксиом 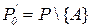 , надо доказать, что ни A, ни
, надо доказать, что ни A, ни  нельзя вывести из
нельзя вывести из  . Для этого достаточно построить две модели теории
. Для этого достаточно построить две модели теории  с формулировкой <T0,
с формулировкой <T0,  > так, чтобы в одной из них выполнялось предложение A (это будет модель теории T), а в другой -
> так, чтобы в одной из них выполнялось предложение A (это будет модель теории T), а в другой -  . Так как непротиворечивость теории T считается установленной ранее, то первую модель уже фактически строить не надо. Достаточно построить вторую модель – модель теории с формулировкой
. Так как непротиворечивость теории T считается установленной ранее, то первую модель уже фактически строить не надо. Достаточно построить вторую модель – модель теории с формулировкой 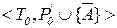 .
.
Например, независимость системы аксиом A1, A2, A3 теории аффинных плоскостей может быть доказана посредством построения трех интерпретаций теории, для каждой из которых не выполняется одна из аксиом A1, A2, A3, а две другие выполняются (рис. 6.1).

Рис. 6.1. Три интерпретации для доказательства независимости
аксиом A1, A2, A3 соответственно
Независимость не является обязательным требованием для системы аксиом. Независимость системы аксиом свидетельствует в известном смысле об изяществе содержащей эту систему формулировки теории. Не всегда для той или иной аксиоматической теории целесообразно выбирать независимую систему аксиом: изящество системы аксиом может привести к громоздкости доказательств теорем теории.
– Конец работы –
Эта тема принадлежит разделу:
АКСИОМАТИЧЕСКИАЯ ТЕОРИЯ
Е П Емельченков В Е Емельченков...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Формулировка аксиоматической теории
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов