рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Вид работы: Лекции
- /
- Критерий согласия Пирсона
Реферат Курсовая Конспект
Критерий согласия Пирсона
Критерий согласия Пирсона - Лекция, раздел Образование, Лекция 2 Оценки параметров распределения Критерий Пирсона Применяется, Если Объем Выборки ...
Критерий Пирсона применяется, если объем выборки  , а интервалы содержат более 5 вариант.
, а интервалы содержат более 5 вариант.
Рассмотрим случайную величину
 ,
,
где  – эмпирическая частота,
– эмпирическая частота,  – теоретическая частота, которая равна
– теоретическая частота, которая равна  , где
, где  – вероятность попадания случайной величины в
– вероятность попадания случайной величины в  –й интервал сгруппированного статистического ряда. Тогда
–й интервал сгруппированного статистического ряда. Тогда
 .
.
Если рассматривать различные выборки, то случайная величина  принимает различные значения. Чем меньше различаются
принимает различные значения. Чем меньше различаются  и
и  , тем меньше
, тем меньше  , следовательно, величина
, следовательно, величина  в известной степени характеризует близость теоретического и эмпирического распределения.
в известной степени характеризует близость теоретического и эмпирического распределения.
Заметим, что возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей, а делением на  достигают уменьшения каждого из слагаемых.
достигают уменьшения каждого из слагаемых.
Доказано, что при 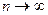 распределение С.В.
распределение С.В.  стремится к закону распределения
стремится к закону распределения  с
с 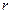 степенями свободы, где
степенями свободы, где  . Здесь
. Здесь  – число интервалов,
– число интервалов, – число параметров распределения (для нормального распределения
– число параметров распределения (для нормального распределения  , для распределения Пуассона
, для распределения Пуассона  ). Плотность распределения
). Плотность распределения  равна
равна
 . где
. где 
По такому закону распределена сумма квадратов 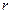 случайных величин, каждая из которых распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией равной единице
случайных величин, каждая из которых распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией равной единице 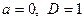 .
.
Множество всех значений критерия  разбивают на 2 непересекающихся множества
разбивают на 2 непересекающихся множества  и
и  , при этом
, при этом  –критическая область –содержит значения критерия, при которых нулевая гипотеза отвергается, а
–критическая область –содержит значения критерия, при которых нулевая гипотеза отвергается, а  – область принятия гипотезы –содержит значения критерия, при которых нулевая гипотеза принимается. Эти области разделяются критической точкой
– область принятия гипотезы –содержит значения критерия, при которых нулевая гипотеза принимается. Эти области разделяются критической точкой 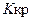 . Гипотеза принимается, если
. Гипотеза принимается, если 
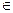
 , и гипотеза отвергается, если
, и гипотеза отвергается, если  .
.
Вероятность ошибки первого рода, т.е.  , называют уровнем значимости критерия
, называют уровнем значимости критерия  . Если
. Если  — вероятность ошибки второго рода, то величину
— вероятность ошибки второго рода, то величину 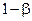 =
= называют мощностью критерия
называют мощностью критерия  .
.
Если проверяемая гипотеза  верна, то
верна, то  . Если известен закон распределения критерия, то точка
. Если известен закон распределения критерия, то точка 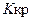 находится из условия
находится из условия  , где
, где  – заданный уровень значимости, т.е. для нахождения критической точки
– заданный уровень значимости, т.е. для нахождения критической точки 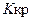 задаются уровнем значимости
задаются уровнем значимости  и требуют, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий
и требуют, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий 
 примет значение большее
примет значение большее 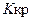 была равна
была равна  .
.  .
.
Существуют подробные таблицы вероятности  при заданном
при заданном  . При практическом использовании критерия
. При практическом использовании критерия  по заданному уровню значимости
по заданному уровню значимости  и числу степеней свободы
и числу степеней свободы 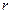 из таблицы находят
из таблицы находят  и сравнивают это значение с
и сравнивают это значение с  . Если
. Если  , то нулевую гипотезу принимают, если же
, то нулевую гипотезу принимают, если же  , то нулевую гипотезу отвергают.
, то нулевую гипотезу отвергают.
Наблюдаемое значение критерия может оказаться большим  не потому, что нулевая гипотеза ложна, а по другим причинам, например, вследствие малого объема выборки. В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода.
не потому, что нулевая гипотеза ложна, а по другим причинам, например, вследствие малого объема выборки. В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода.
Иногда область  принятия гипотезы о законе распределения ограничивают с двух сторон
принятия гипотезы о законе распределения ограничивают с двух сторон  , где
, где 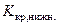 находят из условия
находят из условия  . Тогда гипотеза о виде распределения случайной величины
. Тогда гипотеза о виде распределения случайной величины 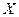 принимается при
принимается при  .
.
Критерий Пирсона применяется для проверки правдоподобия гипотез любых законов распределения. С помощью критерия Пирсона нельзя доказать, что рассматриваемая гипотеза действительно справедлива, критерий указывает лишь на то, что гипотеза не противоречит опытным данным.
Схема применения критерия  для проверки гипотезы
для проверки гипотезы  :
:
1. Для заданной выборки строят вариационный ряд– группированный статистический ряд.
2. Определяется мера расхождения эмпирических и теоретических частот по формуле 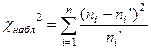 .
.
3. Для уровня значимости  по таблице
по таблице  распределения находят критическое значение
распределения находят критическое значение  , где
, где  – число степеней свободы (
– число степеней свободы ( – число интервалов,
– число интервалов,  – число параметров распределения случайной величины).
– число параметров распределения случайной величины).
4. По той же таблице находят 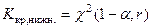 .
.
5. Если  или
или  , то нулевая гипотеза отвергается. Если же
, то нулевая гипотеза отвергается. Если же  , то считают, что гипотеза не противоречит экспериментальным данным.
, то считают, что гипотеза не противоречит экспериментальным данным.
Критерий Пирсона дает удовлетворительные результаты, если объем выборки велик ( и частоты (эмпирические и теоретические) имеют значения не меньше, чем 5. Если для некоторых из интервалов
и частоты (эмпирические и теоретические) имеют значения не меньше, чем 5. Если для некоторых из интервалов  , то следует объединить соседние интервалы. Отметим, что в двух крайних интервалах допускается значение
, то следует объединить соседние интервалы. Отметим, что в двух крайних интервалах допускается значение  .
.
Критерий согласия Колмогорова или критерий 
В качестве меры расхождения теоретического и экспериментального распределений в критерии Колмогорова рассматривается величина 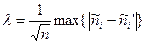 , где
, где
 – накопленные теоретические частоты,
– накопленные теоретические частоты,
 – накопленные экспериментальные частоты,
– накопленные экспериментальные частоты,
Т–объем выборки.
Колмогоров нашел, что при 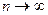

Существуют подробные таблицы  , из которых по заданному
, из которых по заданному  определяют
определяют  .
.
Если  , то нулевую гипотезу принимают.
, то нулевую гипотезу принимают.
Если  , то нулевую гипотезу отвергают.
, то нулевую гипотезу отвергают.
Критерий Колмогорова часто дает несколько завышенные оценки правдоподобности гипотезы. В некоторых случаях можно принять за правдоподобную гипотезу, плохо согласующуюся с опытными данными.
– Конец работы –
Эта тема принадлежит разделу:
Лекция 2 Оценки параметров распределения
На сайте allrefs.net читайте: Лекция 2.
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Критерий согласия Пирсона
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов