Линейные преобразования. Их запись матрицами.
1) Линейные преобразования. Их запись матрицами.
Пусть 
-- 
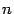-мерное линейное пространство, в котором задан базис 
,
-- линейное преобразование. Возьмем произвольный вектор 
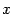. Пусть 
-- его координатный столбец. Координатный столбец вектора 
обозначим 
.
Запишем разложение вектора 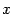по базису пространства 
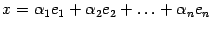. Для образа этого вектора получим
| (19.2) |
Векторы 
имеют какие-то координатные столбцы, обозначим
их 
, 
, ..., 
соответственно. В этой записи первый индекс показывает номер координаты, а второй индекс -- номер вектора. Соответственно,
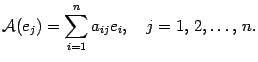
Подставим это выражение в равенство (19.2) и, изменим порядок суммирования
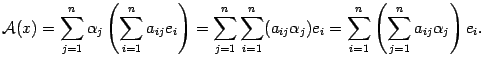
Это равенство означает, что 
-той координатой вектора служит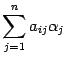 
.
Составим матрицу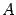 
из координатных столбцов векторов 
, ..., 
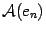
Вычислим произведение матрицы 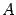на столбец 
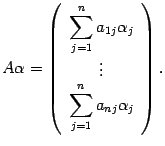
Мы видим, что -ый элемент столбца совпадает с -ой координатой вектора . Поэтому
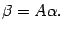
| (19.3) |
Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора.
Матрица 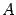называется матрицей линейного преобразования . Еще раз напомним, как она составлена: первый столбец является координатным столбцом образа первого базисного вектора, второй столбец -- координатным столбцом образа второго базисного вектора и т.д.
2) Закон умножения матриц как композиций линейных преобразований. Ассоциативность умножения
Операции над матрицами
Умножение матрицы на число
Свойства умножения матриц на число: § 1. 1A = A;Решение систем линейных уравнений. Однородные и неоднородные уравнения. Различные методы решения
или: .Однородные системы
Однородной системой линейных уравнений называется система вида:
Нулевое решение 
системы (1) называется тривиальным решением.
Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.
Если существует любое ненулевое решение системы, то оно называется нетривиальным.
Неоднородные системы
— её расширенная матрица. § Ме́тод Га́усса[1] — классический метод решения системы линейных уравнений (СЛУ). Это метод…Пример
Система линейных уравнений:
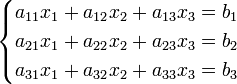
Определители:
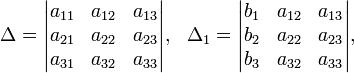
Решение:
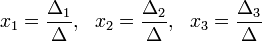
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с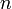 
неизвестными (над произвольным полем):
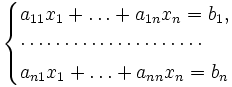
Тогда её можно переписать в матричной форме:
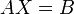, где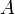 
— основная матрица системы, 
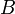и 
— столбцы свободных членов и решений системы соответственно:
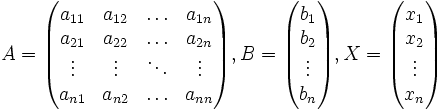
Умножим это матричное уравнение слева на 
— матрицу, обратную к матрице :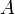 
Так как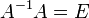 
, получаем 
. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность
.
6) Основная теорема арифметики.
Основная теорема арифметики
Любое составное число можно единственным (с точностью до перестановки сомножителей) образом представить в виде произведения простых чисел