Определение. Разбиением с отмеченными точками называется разбиение и набор точек
Определенный интеграл
Определение. Разбиением 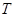 отрезка
отрезка 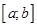 называется набор точек
называется набор точек 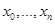 этого отрезка такой, что
этого отрезка такой, что 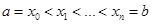 .
.
Отрезки 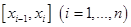 называются отрезками разбиения.
называются отрезками разбиения.
Максимум 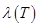 из длин отрезков разбиения называется параметром разбиения.
из длин отрезков разбиения называется параметром разбиения.
Определение. Разбиением с отмеченными точками  называется разбиение
называется разбиение 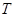 и набор точек
и набор точек 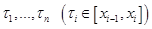 .
.
Определение. Пусть функция 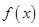 определена на отрезке
определена на отрезке 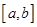 , а
, а  - разбиение с отмеченными точками этого отрезка. Сумма
- разбиение с отмеченными точками этого отрезка. Сумма
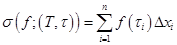 ,
,
где 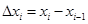 , называется интегральной суммой функции
, называется интегральной суммой функции  , соответствующей разбиению с отмеченными точками
, соответствующей разбиению с отмеченными точками  .
.
Определение. Говорят, что число 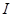 является интегралом Римана от функции
является интегралом Римана от функции  на отрезке
на отрезке 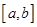 , если для любого
, если для любого  найдется такое
найдется такое 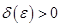 , что для любого разбиения
, что для любого разбиения  с отмеченными точками отрезка
с отмеченными точками отрезка 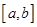 , параметр разбиения которого
, параметр разбиения которого 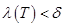 , имеет место соотношение
, имеет место соотношение
 .
.
Интеграл от функции 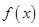 по отрезку
по отрезку 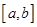 обозначается символом
обозначается символом 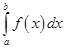 , числа
, числа  и
и  называются верхним и нижним пределом интегрирования соответственно;
называются верхним и нижним пределом интегрирования соответственно;
 - подынтегральная функция,
- подынтегральная функция,  - подынтегральное выражение,
- подынтегральное выражение,  - переменная интегрирования.
- переменная интегрирования.
Таким образом,
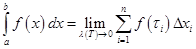 .
.
Определение. Функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке 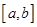 , если для нее определен интеграл Римана.
, если для нее определен интеграл Римана.
Необходимое условие интегрируемости.
Утверждение. Если функция  , определенная на отрезке
, определенная на отрезке 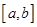 , интегрируема на нем, то она ограничена на этом отрезке.
, интегрируема на нем, то она ограничена на этом отрезке.
Доказательство. 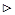 Если
Если  неограниченна на
неограниченна на 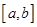 , то при любом разбиении
, то при любом разбиении 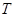 функция будет неограниченной по крайней мере на одном из отрезков
функция будет неограниченной по крайней мере на одном из отрезков 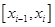 . Это означает, что, выбирая соответствующим образом точку
. Это означает, что, выбирая соответствующим образом точку 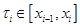 , можно сделать величину
, можно сделать величину 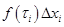 сколь угодно большой, но тогда и интегральную сумму
сколь угодно большой, но тогда и интегральную сумму 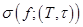 можно сделать сколь угодно большой по модулю, что означает, что конечного предела у интегральных сумм нет.
можно сделать сколь угодно большой по модулю, что означает, что конечного предела у интегральных сумм нет.
Суммы Дарбу.
. Эти суммы называются, соответственно, нижней и верхней интегральными суммами,…Свойства сумм Дарбу.
Доказательство. Для доказательства этого факта достаточно ограничиться присоединением одной точки . Пусть она попала на й промежуток: . Обозначим через новую верхнюю сумму Дарбу, от прежней она отличается только слагаемыми, соответствующими промежутку .…Условие существования интеграла.
Доказательство. Необходимость. Предположим, что интеграл существует, то есть , причем предел здесь берется по всем интегральным суммам, а, значит, и . Достаточность. Пусть теперь . Тогда, перейдя в неравенствах (и здесь строятся по одному разбиению) к пределу, получим…Классы интегрируемых функций.
Теорема. Если функция непрерывна на отрезке 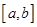 , то она интегрируема на нем.
, то она интегрируема на нем.
Доказательство.  Непрерывная на отрезке функция равномерно непрерывна на нем (теорема Кантора). То есть по заданному
Непрерывная на отрезке функция равномерно непрерывна на нем (теорема Кантора). То есть по заданному  найдется такое
найдется такое  , что из
, что из  следует
следует 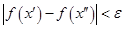 . Но тогда, если
. Но тогда, если 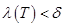 , то
, то 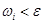 и
и
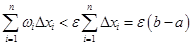 ,
,
откуда следует существование интеграла.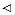
Справедливо также следующее утверждение.
Теорема. Если ограниченная на отрезке функция имеет на нем лишь конечное число точек разрыва, то она интегрируема на этом отрезке.
Пример. Функция 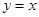 непрерывна на отрезке
непрерывна на отрезке 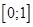 , а значит интегрируема на нем. Интеграл
, а значит интегрируема на нем. Интеграл 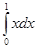 будет пределом любой последовательности интегральных сумм с
будет пределом любой последовательности интегральных сумм с  . Рассмотрим последовательность разбиений
. Рассмотрим последовательность разбиений 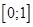 на равные отрезки:
на равные отрезки: 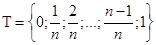 и выделим точки
и выделим точки 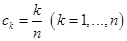 . Тогда
. Тогда
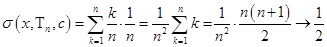 при
при 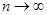 . То есть
. То есть 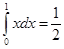 .
.