рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Свойства и вычисление определенных интегралов.
Реферат Курсовая Конспект
Свойства и вычисление определенных интегралов.
Свойства и вычисление определенных интегралов. - раздел Математика, Задачи, приводящие к понятию определенного интеграла Начнем С Того, Что Введем Понятие Определенного Интеграла Без...
Начнем с того, что введем понятие определенного интеграла без привязки его к каким-либо геометрическим, физическим и экономическим задачам (что было сделано выше ). То есть введем его сугубо математически.
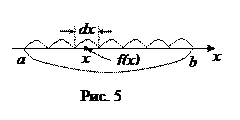 Пусть
Пусть 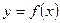 - некоторая непрерывная функция, заданная на некотором числовом промежутке [а; b] оси ox. Разобьем его на бесконечно большое число бесконечно малых участков длиной
- некоторая непрерывная функция, заданная на некотором числовом промежутке [а; b] оси ox. Разобьем его на бесконечно большое число бесконечно малых участков длиной  и выберем на каждом
и выберем на каждом  некоторую точку
некоторую точку  . Так как каждый из этих участков бесконечно мал (то есть фактически представляет собой точку), то
. Так как каждый из этих участков бесконечно мал (то есть фактически представляет собой точку), то 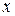 и есть эта точка. Тогда
и есть эта точка. Тогда 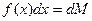 - бесконечно малое число (смысл его зависит от смысла функции
- бесконечно малое число (смысл его зависит от смысла функции 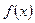 и может быть самым разным - см. предыдущий параграф). А сумма всех этих бесконечно малых чисел
и может быть самым разным - см. предыдущий параграф). А сумма всех этих бесконечно малых чисел 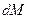 называется определенным интегралом
называется определенным интегралом
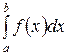 (17)
(17)
от функции 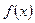 с пределами интегрирования
с пределами интегрирования  и
и 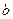 (нижним и верхним).
(нижним и верхним).
Ниже мы покажем, что при непрерывной подынтегральной функции 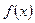 и конечных пределах интегрирования а и b определенный интеграл (13) заведомо существует (представляет собой некоторое конечное число
и конечных пределах интегрирования а и b определенный интеграл (13) заведомо существует (представляет собой некоторое конечное число 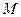 ). То есть при указанных условиях
). То есть при указанных условиях
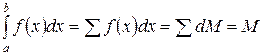 - число. (18)
- число. (18)
 Равенство (18) будем считать математическим определением определенного интеграла. Определенным он называется потому, что в отличие от неопределенного интеграла
Равенство (18) будем считать математическим определением определенного интеграла. Определенным он называется потому, что в отличие от неопределенного интеграла 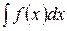 , представляющего собой бесчисленное множество функций, он представляет собой вполне определенное число. Таким образом, несмотря на внешнее сходство в обозначениях определенного и неопределенного интегралов, это совершенно разные вещи. Впрочем, как это ни удивительно, между ними имеется связь. Но об этом мы поговорим несколько позже.
, представляющего собой бесчисленное множество функций, он представляет собой вполне определенное число. Таким образом, несмотря на внешнее сходство в обозначениях определенного и неопределенного интегралов, это совершенно разные вещи. Впрочем, как это ни удивительно, между ними имеется связь. Но об этом мы поговорим несколько позже.
А сейчас подтвердим, что в случае непрерывной подынтегральной функции и конечных пределов интегрирования определенный интеграл (17) действительно представляет собой некоторое конечное число. Для этого рассмотрим все возможные случаи относительно функции 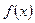 .
.
а) Пусть непрерывная функция 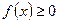 для всех
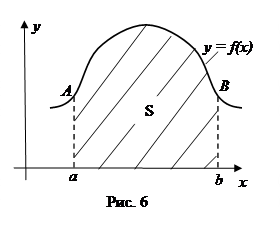
для всех 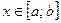 . Тогда, согласно (4), определенный интеграл (17) можно представлять себе как площадь
. Тогда, согласно (4), определенный интеграл (17) можно представлять себе как площадь 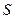 криволинейной трапеции (рис.6). И эта площадь S заведомо представляет собой число:
криволинейной трапеции (рис.6). И эта площадь S заведомо представляет собой число:
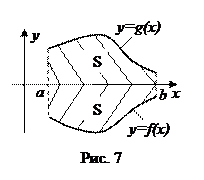
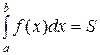 - число (19)
- число (19)
б) Пусть непрерывная функция 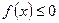 для всех
для всех 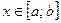 . Тогда функция
. Тогда функция 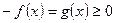 для всех
для всех 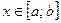 (см. рис. 5). В этом случае
(см. рис. 5). В этом случае
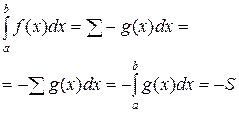 (20)
(20)
То есть и в этом случае 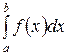 - число (только отрицательное). А именно, этот интеграл, как и в случае (а), представляет собой площадь
- число (только отрицательное). А именно, этот интеграл, как и в случае (а), представляет собой площадь 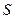 криволинейной трапеции, заключенной между осью ох и графиком функции
криволинейной трапеции, заключенной между осью ох и графиком функции 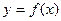 , только со знаком минус (рис. 8):
, только со знаком минус (рис. 8):
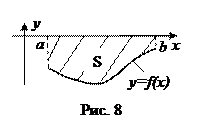
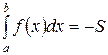 (21)
(21)
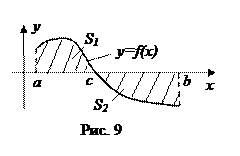 в) Наконец, если на части
в) Наконец, если на части 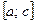 отрезка
отрезка 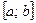 функция
функция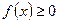 , а на другой части
, а на другой части 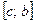 этого отрезка функция
этого отрезка функция 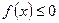 (рис 9), то
(рис 9), то
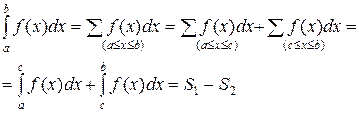 То есть и в этом случае
То есть и в этом случае  представляет собой число.
представляет собой число.
Итак, подтверждение получено: для любой непрерывной на конечном промежутке 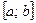 функции f(x) определенный интеграл
функции f(x) определенный интеграл  существует (представляет собой некоторое число).
существует (представляет собой некоторое число).
Заметим, что определенные интегралы рассматривают и для разрывных подынтегральных функций, а также тогда, когда пределы интегрирования бесконечные. В таких случаях определенные интегралы могут и не существовать. Об этих интегралах мы поговорим позднее.
– Конец работы –
Эта тема принадлежит разделу:
Задачи, приводящие к понятию определенного интеграла
Задачи приводящие к понятию определенного интеграла Задача о вычислении площади произвольной...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свойства и вычисление определенных интегралов.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов