Интегрирование линейных ДУ высших порядков
Лекция № 17
Интегрирование линейных ДУ высших порядков.
Уравнения, допускающие понижение порядка
Уравнения вида (1.1) решается путем n – кратного интегрирования. Уравнение , (1.2)Пример1.1 Решить уравнение .
Решение (аналитическое).
В левой части этого уравнения стоит третья производная искомой функции, в правой – функция только от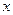 
, это уравнение вида (1.1).
Т.к. 
, то 
, 
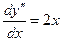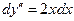, откуда 
.
Поскольку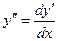 
, то последнее уравнение можно переписать так:
, 
, откуда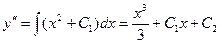
или 
.
Интегрируя еще раз, находим общее решение исходного уравнения 
.
Решение в среде MATLAB.
(Синтаксис команд MATLAB будет приведен ниже.)
1.Решим уравнение аналитически
>> dsolve('D3y=t*2')
ans =1/12*t^4+1/2*C1*t^2+C2*t+C3.
Как видно, ответ совпадает с точностью до названия переменной.
2.Решим уравнение численно и построим его график.
Для этого необходимо составить задачу Коши (т.е. задать начальные условия),а также интервал интегрирования и построения графика.
- Создаем m.- файл, где задаем условие уравнения:
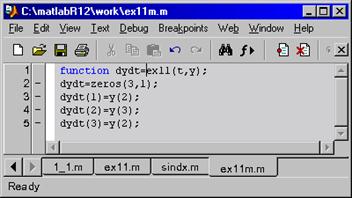
- Задаем интервал интегрирования, начальные условия, и производим поиск решения.
>> tspan=[0 20];
>> y0=[1 1 1];
>> [t,y]=ode45('ex11',tspan,y0);
>> plot(t,y)
Пример 1.2 Решить уравнение .
Решим уравнение аналитически. Это уравнение вида (1.2) , для которого 
, 
.
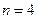Принимая низшую производную 
за новую неизвестную функцию 
, осуществим подстановку (1.3):
,откуда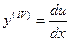 
. Т.о., данное уравнение сводится к уравнению первого порядка относительно : 
или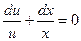 
, из которого получаем 
, в котором правая часть зависит только от 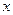, т.е. уравнение вида(1.1).
Трижды интегрируя, получаем соответственно: 
; 
;
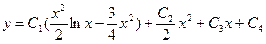;или 
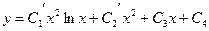, где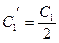 
, 
.
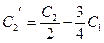Решение в среде MATLAB.
1.Решим уравнение аналитически
>> dsolve('D4y*t+D3y=0')
ans = C1+C2*t+C3*t^2+C4*t^2*log(t)
2.Решим уравнение численно и построим его график.
Для этого необходимо составить задачу Коши (т.е. задать начальные условия),
а также интервал интегрирования и построения графика.
Создаем m.- файл, где задаем условие уравнения:
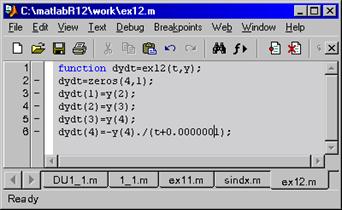
Для избежания деления на 0 и «зацикливания» программы, добавляем к t малую величину 0,0000001, не влияющую, в общем, на численное решение.
Задаем интервал интегрирования, начальные условия, и производим поиск решения.
>> y0=[1 1 1 1];
>> tspan=[0 20];
>> [T,Y]=ode45('ex12',tspan,y0);
>> plot(T,Y(:,1))
Пример 1.3 Определить тип уравнения и метод решения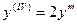 
Это уравнение вида (1.2). Положим 
, тогда 
, поэтому уравнение имеет вид
, 
.
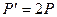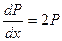Пример 1.4 Решить дифференциальное уравнение 
Решим уравнение аналитически. Это уравнение вида (1.5) решаем с помощью подстановки 
Получаем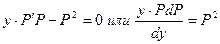 
. Отсюда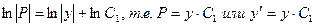 
Подставляем начальные условия 
. Имеем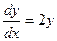 
. Решая, получаем 
. Подставляем начальные условия 
. 
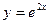- частное решение дифференциального уравнения.
Аналитическое решение в среде Matlab.
>> y=dsolve('y*D2y-Dy^2=0','y(0)=1','Dy(0)=2','x')
y = exp(2*x)
Численное решение в среде Matlab.
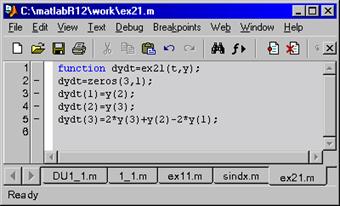
Создаем m.- файл, где задаем условие уравнения:
function dydt=pr7(t,y);
dydt=zeros(2,1);
dydt(1)=y(2);
dydt(2)=y(2).^2./(y(1)+0.0000001); % Для избежания деления на 0 и «зацикливания» программы
Задаем интервал интегрирования, начальные условия, и производим поиск решения.
>> y0=[1 2];
>> tspan=[0 1];
>> [t,y]=ode45('pr7',tspan,y0);
Линейные однородные уравнения с постоянными коэффициентами
Дифференциальное уравнение , (2.1) где - постоянные величины, называется линейным однородным уравнением - го… где - его линейно независимые частные решения. Последние находятся с помощью характеристического уравнения. (2.3)Пример 2.1 Решить уравнение .
Решение (аналитическое).
Для данного уравнения с постоянными коэффициентами составим характеристическое уравнение( при этом нужно сохранить коэффициенты, вместо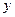 
поставить 1, вместо ее производной 
-того порядка поставить 
): 
.
Преобразуя правую часть уравнения , получим 
,
откуда 
.
В соответствии с формулой (2.5) получаем общее решение 
.
Решение в MATLAB.
Аналитическое:
>> dsolve('D3y-2*D2y-Dy+2*y=0')
ans = C1*exp(t)+C2*exp(2*t)+C3*exp(-t)
Численное:
>> y0=[1 1 1 ];
>> tspan=[0 20];
>> [T,Y]=ode45('ex21',tspan,y0);
>> plot(T,Y)
Пример 2.2Решить уравнение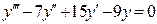 
.
Решение. Составим характеристическое уравнение 
,
один из корней которого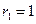 
можно получить методом проб.
Так как 
,
то уравнение принимает вид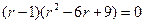 
,
откуда 
. таким образом, характеристическое уравнение имеет один простой (однократный 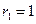) корень и двукратный корень 
.В соответствии с формулами (2.6) и (2.2) получаем общее решение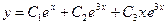 
.
MATLAB >> dsolve('D3y-7*D2y+15*Dy-9*y=0') ans = C1*exp(t)+C2*exp(3*t)+C3*exp(3*t)*t
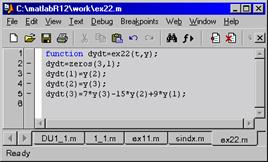
>> y0=[2 0.5 0];
>> tspan=[0 10];
>> [T,Y]=ode45('ex21',tspan,y0);
>> plot(T,Y(:,1))
Пример 2.3 Решить уравнение .
Решение . Характеристическое уравнение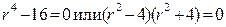 
имеет корни 
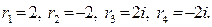Мнимым сопряженным корням 
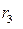и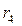 
(для которых 
,
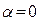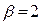) соответствуют частные решения 
,полученные из формул (2.7).
Таким образом, общее решение имеет вид 
.
Решение в MATLAB
>> dsolve('D4y-16*y=0')
ans = C1*cos(2*t)+C2*sin(2*t)+C3*exp(2*t)+C4*exp(-2*t)
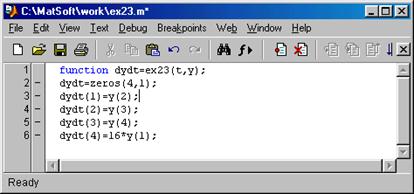
>> y0
y0 = -5.0000 0.3300 7.0000 -5.0000
>> tspan=[0 1];
>> [t,y]=ode45('ex23',tspan,y0);
>> plot(t,y(:,1))
Пример 2.4 Решить уравнение .
Составим характеристическое уравнение, соответствующее данному дифференциальному уравнению:
.
Преобразуя левую часть этого уравнения , получим 
или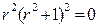 
.
Таким образом характеристическое уравнение 
имеет один двукратный действительный корень 
и пару двукратных мнимых сопряженных корней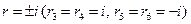 
. По формулам (2.8), (2.2) и (2.6) получаем общее решение 
.
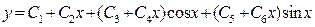Решение в MATLAB
>> dsolve('D6y+2*D4y+D2y=0')
ans = C1+C2*t+C3*cos(t)+C4*sin(t)+C5*cos(t)*t+C6*sin(t)*t
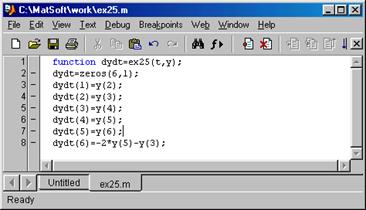
>> tspan=[0 5];
>> y0=[-1 1 0 -5 0 10];
>> [t,y]=ode45('ex25',tspan,y0);
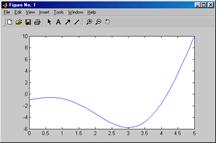
>> plot(t,y(:,1))
Линейные неоднородные уравнения с постоянными коэффициентами
Дифференциальное уравнение (3.1) называется линейным неоднородным уравнением с постоянными коэффициентами .Пример 3.2 Решить уравнение .
Решение. Характеристическое уравнение 
имеет корни 
поэтому
Поэтому общее решение выразится формулой 
.
Методом вариации произвольных постоянных находим общее решение данного неоднородного уравнения, полагая 
.
Система (3.13) для определения функций 
запишется так
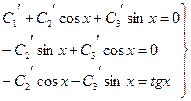
Умножив обе части второго уравнения на 
, третьего на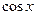 
и сложив почленно, получим
. Из второго уравнения имеем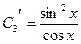 
. Сложив почленно первое уравнение с третьим, получим 
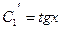. Интегрируя три полученных уравнения, находим: 
; 
; 
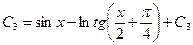, где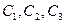 
- произвольные постоянные.
Следовательно, общее решение данного неоднородного уравнения выразиться формулой
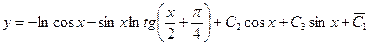, где 
.
>> dsolve('D3y+Dy=tan(t)')
ans = 1/2-log(cos(t))-sin(t)*log((1+sin(t))/cos(t))+C1+C2*cos(t)+C3*sin(t)
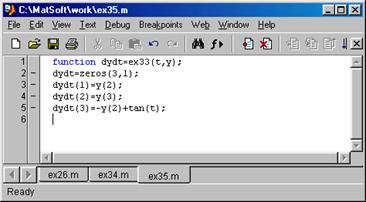
>> y0=[-10 -1 -1];
>> tspan=[-3 1.5];
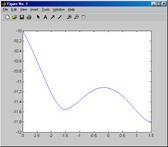
>> [t,y]=ode45('ex35',tspan,y0);
>> plot(t,y(:,1))