Линейные неоднородные уравнения с постоянными коэффициентами

1.3.1. Теоретическая справка

Дифференциальное уравнение

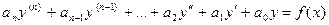(3.1)

называется линейным неоднородным уравнением с постоянными коэффициентами .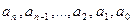

Если 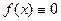, то уравнение (3.1) становится однородным:

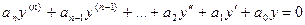. (3.2)

Общее решение уравнения (3.1) определяется формулой

, (3.3)

где 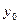- общее решение соответствующего однородного уравнения (3.2), а - частное решение данного неоднородного уравнения.

В простейших случаях частное решение может быть найдено с помощью метода неопределенных коэффициентов. Если , (3.4)

где - многочлен степени 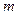, то частное решение ищут в виде

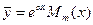, (3.5)

где 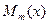- многочлен той же степени с неопределенными коэффициентами, если 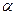не является корнем характеристического уравнения, соответствующего уравнению (3.2), и в виде

, (3.6)

если 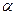- корень указанного уравнения кратности

В частности, при 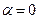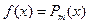и если 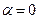не является корнем характеристического уравнения, то существует частное решение 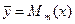, если 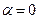- корень характеристического уравнения кратности , то .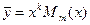

Если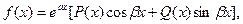 (3.7)

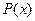где и 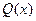- многочлены, наибольшая степень которых 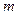, то частное решение ищут в виде

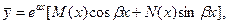(3.8)

если не является корнем характеристического уравнения, и в виде

(3.9)

где и 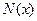- многочлены степени 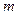, если - корень указанного уравнения кратности .

Если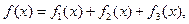 (3.10)

где 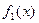, , 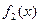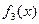- функции вида (3.4) и (3.7), то существует частное решение

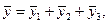(3.11)

определяемое указанными выше правилами.

 

В общем случае частное решение уравнения (3.1) может быть найдено с помощью метода вариации произвольных постоянных (метода Лагранжа). Если

общее решение однородного уравнения (3.2), то общее решение неоднородного уравнения (3.1) ищут в виде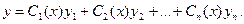 (3.12)

Функции 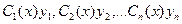находят из системы уравнений:

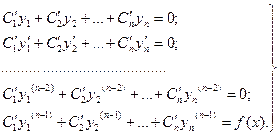(3.13)

 

Пример 3.1. Решить уравнение .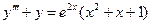

Решение. Это линейное неоднородное уравнение третьего порядка с постоянными коэффициентами, правая часть которого есть функция вида (3.4), гд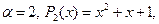е т.е. .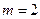

Найдем сначала общее решение соответствующего однородного уравнения .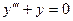

Так как характеристическое уравнение 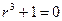имеет корни 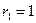, , 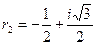, 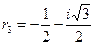то общее решение однородного уравнения определяется формулой

.

В соответствии с формулой (3.5) частное решение исходного уравнения ищем в виде

,

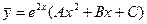поскольку число 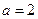не является корнем характеристического уравнения 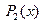- многочлен второй степени.

Находим производные функции :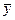

;

;

.

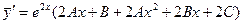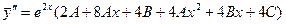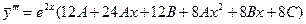Подставляя выражения для 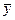и 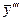в данное уравнение и сокращая на 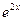, получим тождество

,

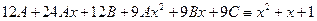откуда

и ,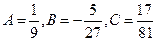

поэтому .

Общее решение данного уравнения имеет вид

.

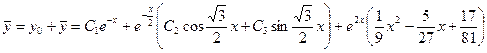Решение в MATLAB

>> dsolve('D3y+y=(e^2*t)*(t^2+t+1)')

Решение в Matlab

ans = -6*e^2+e^2*t+e^2*t^2+e^2*t^3+C1*exp(-t)+C2*exp(1/2*t)*sin(1/2*3^(1/2)*t)+C3*exp(1/2*t)*cos(1/2*3^(1/2)*t)

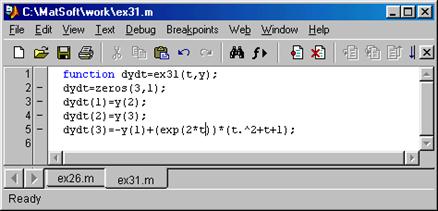
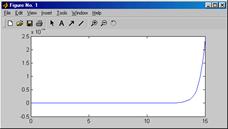
>> y0=[-0.1 -1 1];

>> tspan=[0 15];

>> [t,y]=ode45('ex31',tspan,y0);

>> plot(t,y(:,1))