Элементы математической логики

Элементы математической логики

В повседневной жизни процесс вывода заключений происходит в большей степени подсознательно, интуитивно, в соответствии с на­копленным индивидуальным… Тем не менее, все возрастающее число задач научной, технической и… Термин «логика» про­исходит от греческого слова логос, что означает «мысль», «разум», «слово», «понятие». Логика (или…

Алгебра высказываний.

Высказывания и операции над ними

1.1 Понятие высказывания.Основным понятием математической логики является понятие «простого высказывания». Под высказываниемпонимается предложение, представляющее собой такое утверждение, о котором можно судить, истинно оно или ложно. Логическими значениями высказываний являются «истина» и «ложь».

Приведем примеры высказываний.

1. Москва – столица России.

2. Омск находится на берегу Волги.

3. 3+2=5.

4. Кислород – газ.

5. 3<2.

Высказывания 1), 3), 4) истинны, а высказывания 2), 5) ложны.

Не всякое предложение является высказыванием. К высказываниям не относятся вопросительные и восклицательные предложения. Предложения «Математика – интересный предмет», «Осень – лучшая пора года» не являются высказываниями, так как нет единого мнения о том, истинны эти предложения или ложны. Предложения «Сегодня плохая погода», «3х<2» также не являются высказываниями, для того чтобы определить их истинность или ложность, нужны дополнительные сведения: конкретный день, о котором идет речь; значение, которое принимает х.

Высказывания, представляющие собой одно утверждение, называют простым или элементарным. Из элементарных высказываний с помощью логических связок можно построить высказывания, называемые сложными или составными. Образование составного высказывания с помощью логической связки называют логической операцией.

Из элементарных высказываний можно получить составные с помощью логических связок «не», «неверно, что», «и», «или», «если…, то…», «либо», «тогда и только тогда». Остальные логические связки либо близки по смыслу к каким-либо указанным, либо могут быть заменены их комбинацией. Например, союзы «а», «но» близки по смыслу союзу «и».

Так, из элементарных высказываний «На улице светит солнце» и «В классе идут занятия» можно образовать следующие составные высказывания: «На улице светит солнце, и в классе идут занятия»; «В классе не идут занятия, а на улице светит солнце»; «На улице светит солнце, или в классе идут занятия»; «Если на улице светит солнце, то в классе идут занятия»; «На улице светит солнце тогда и только тогда, когда в классе идут занятия».

В алгебре высказываний все высказывания рассматриваются не с точки зрения их содержания, а с точки зрения их истинности или ложности, то есть их логического значения. Каждое высказывание либо истинно, либо ложно, ни одно высказывание не может быть одновременно и истинным, и ложным. Истинное значение высказывания обозначают буквой и (истина) или символом 1, ложное значение – буквой л (ложь) или символом 0.

Логические операции над высказываниями.

Над высказываниями определяются следующие основные логические операции, которые позволяют из имеющихся высказываний строить новые сложные высказывания: 1) отрицание (инверсия); 2) конъюнкция; 3) дизъюнкция; 4) импликация; 5) эквиваленция.

Отрицание (инверсия).

  А   Примеры.

Конъюнкция (логическое умножение).

  А В А / В …   Примеры.

Импликация.

В высказывании высказывание А называется условием или по­сылкой , а высказывание В – следствием или заключением импликации. Логическое значение…   А В …  

Эквиваленция.

  Примеры. 1. Для высказываний «Омск находится на берегу Волги», «2<3» их эквиваленцией будет высказывание «Омск находится на…

Формулы алгебры логики.

Такая схема построения со­ставного высказывания может быть применена к различ­ным конкретным высказываниям, а не только к высказы­ваниям А, В, С .… Теперь сформулируем точное определение формулы ал­гебры высказываний. Определение формулы алгебры высказываний.

Равносильные формулы алгебры логики

Классификация формул алгебры высказываний.

Формула Х называется тождественно истинной (или тавтологией), если она превращается в истинное высказывание, то есть принимает значение 1, при всех наборах значений входящих в нее переменных. Тавтологии представляют собой схемы построения истинных высказываний, независимо от содержания и истинности составляющих элементарных высказываний.

Формула Х называется тождественно ложной, если она принимает значение 0 при всех наборах значений входящих в нее переменных.

Две формулы алгебры логики X и Y называются рав­носильными, если при любых значениях входящих в них высказывательных переменных логические значения высказываний, получающихся из формул X и Y , совпадают. Для указания равносильности формул использу­ют обозначение .

Существует тесная связь между понятием равно­сильности формул и понятием тавтологии.

Признак равносильности формул. Две формулы X и Y алгебры высказываний равносильны тогда и только тогда, когда формула 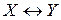является тавто­логией, и обратно, если формула 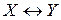– тавтология, то формулы X и Y равносильны.

Отношение равносильности между формулами алгебры высказываний:

а) рефлексивно: ;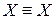

б) симметрично: если , то ;

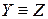в) транзитивно: если и , то .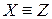

 

 

3.2 Примеры равносильных формул. Равносильности формул алгебры логики часто называют законами логики.

Вот наиболее важные из них:

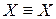1. – закон тождества.
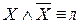2. – закон противоречия.
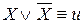3. – закон исключенного третьего.
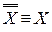4. – закон двойного отрицания.
5. .
6. .
7. .
8. .
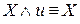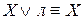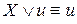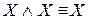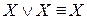9. ; – законы идемпотентности.
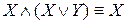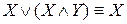10. ; – законы поглощения.
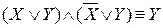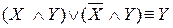11. ; – законы склеивания.
12. законы коммутативности (переместительности):

– коммутативность конъюнкции;

– коммутативность дизъюнкции.

1. законы ассоциативности (сочетательности):

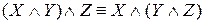– ассоциативность конъюнкции;

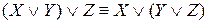– ассоциативность дизъюнкции.

1. законы дистрибутивности (распределительности):

– дистрибутивность конъюнкции относительно дизъюнкции;

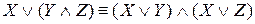– дистрибутивность дизъюнкции относительно конъюнкции.

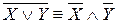1. ; – законы де Моргана.

Доказать эти равносильности можно, например, с помощью таблиц истинности.

 

 

Пример.

Докажем равносильность – закон де Моргана. При любых комбинациях значений, от которых зависят формулы X и Y , эти формулы принимают некоторые логические значения. Всего будет четыре способа распределения логических значений X и Y . Надо показать, что в каждом из этих случаев значения левой и правой части равносильности совпадают.

X	Y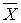

 

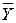
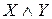
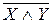
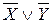
Логические значения в последних двух столбцах совпадают, следовательно, закон де Моргана справедлив.

Имеют место равносильности, выражающие одни логические операции через другие.

Импликациявыражается через:

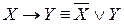1. – дизъюнкцию и отрицание;
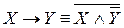2. – конъюнкцию и отрицание.

Эквиваленция выражается через:

1. – конъюнкцию и импликацию;
2. – конъюнкцию, дизъюнкцию и отрицание;
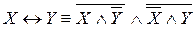3. – конъюнкцию и отрицание.

Из этих равносильностей следует вывод, что любую формулу алгебры логики можно заменить равносильной ей формулой, которая будет содержать только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Дальнейшее исключение логических операций невозможно.

Существует логическая операция, через которую можно выразить любую из пяти логических операций, которыми мы пользуемся: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Эта операция называется «штрих Шеффера», обозначается символом 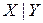и определяется таблицей истинности

 

X	Y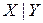

 

Согласно таблице, имеем: ; .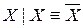

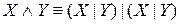Равносильные преобразования формул.

Равносильные преобразования применяются, прежде всего, для упрощения формул. Полученная в результате упрощений формула не должна содержать знаки и ,… Равносильные преобразования формул применяются также для приведения формул к… Отметим, что если некоторая формула является тавтологией, то и всякая равносильная ей формула также является…

Решение логических задач

Методами алгебры логики.

 

Суть применения методов алгебры логики к решению логических задач состоит в том, что, имея конкретные условия логической задачи, стараются записать их в виде формулы алгебры логике. В дальнейшем путем равносиль­ных преобразований упрощают полученную формулу. Простейший вид формулы, как правило, приводит к от­вету на все вопросы задачи.