рефераты конспекты курсовые дипломные лекции шпоры

Раздел Механика
/
Узловой метод получения математических моделей систем

Реферат Курсовая Конспект

Выберите учебное заведение

Узловой метод получения математических моделей систем

Узловой метод получения математических моделей систем - раздел Механика, МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕХНИЧЕСКИХ ОБЪЕКТОВ Узловой Метод Является Популярным При Создании Программных Комплексов Анализа...

Узловой метод является популярным при создании программных комплексов анализа динамических систем. В качестве вектора базисных координат в этом методе используется вектор переменных типа узловых потенциалов, в качестве топологических уравнений - уравнения типа первого закона Кирхгофа.

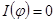(7),

где - вектор переменных, величин типа потенциала, характеризующих состояние узла (скорости, давления, температуры); I - вектор переменных величин типа потока (токи, силы, расходы, тепловые потоки).

Топологические уравнения типа (7) могут быть получены с помощью матрицы инциденций А:

(8)

Из уравнений обобщенного метода получения топологических уравнений уравнение (8) может быть выведено следующим образом. В эквивалентную схему объекта вводятся фиктивные ветви, связывающие все узлы схемы с базовым (базовым может быть любой узел эквивалентной схемы; как правило, это узел, к которому подключено наибольшее количество ветвей). Проводимости этих ветвей равны нулю, т. е. переменная типа I в этих ветвях равна нулю. В дерево включается только эти фиктивные ветви.

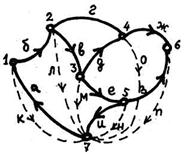
Рис. 5. Матрица инциденций графа.

Для графа, изображенного на рис. 5, без учета ветвей, отмеченных пунктиром, построим матицу инциденций А (таблица 7).

Таблица 7.

а	б	в	г	д	е	ж	з	и
-1	+1
	-1	+1	+1
		-1		+1	+1
			-1	-1		+1
					-1		+1	+1
						-1	-1

Для этого же графа с учетом того, что ветви, отмеченные пунктирными линиями, являются его деревом, построим М-матрицу (таблица 8).

Таблица 8.

	к	л	м	о	н	п
а	+1
б	-1	+1
в		-1	+1
г		-1		+1
д			-1	+1
е			-1		+1
ж				-1		-1
з					-1	+1
и					-1

Фиктивные ветви в эквивалентной схеме имеют направление от небазового узла к базовому.

Сравним полученную М-матрицу с матрицей инциденций А. Если каждой фиктивной ветви поставить в соответствие узел, из которого она выходит, то .

Преобразуем общие топологические уравнения:

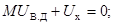(1)

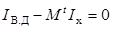(2)

Так как ветви дерева фиктивные, то и из уравнения (2) получим , где I - вектор переменных типа потока реальных ветвей.

Из уравнения (1) получим уравнение связи переменных типа потенциала 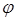с переменными типа разности потенциалов U на реальных ветвях. Так как 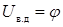, то или .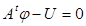

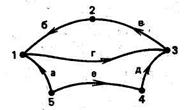
Рис. 6. Граф.

В узловом методе в вектор неизвестных включается вектор или 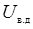, компонентные уравнения алгебраизуются так же, как и в табличном методе, но накладывается ограничение на вид компонентного уравнения: оно обязательно должно быть представлено в виде зависимости переменной типа потока от переменной типа потенциала, т.е. 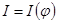, либо от времени.

Тогда алгебраизованная и линеаризованная система уравнений приобретает вид

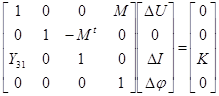(9)

где - матрица частных производных компонентных уравнений по переменным типа разности потенциалов; К - вектор невязок компонентных уравнений.

Исключим из вектора неизвестных подвекторы и . Из первого уравнения системы (9) имеем 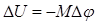. Подставим это значение в третье уравнение системы, а полученный результат - во второе: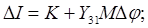 , или

(10)

где - матрица Якоби (матрица узловых проводимостей), алгоритм экономического вычисления которой будет рассмотрен ниже; 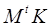- вектор сумм переменных типа потока в узлах схемы.

Уравнение (10) и есть линеаризованная MMС для узлового метода.

Рассмотрим, что представляет собой матрица .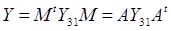

Для графа, показанного на рис. 6, построим матрицу инциденций (таблица 9), приняв за базовый узел 5.

Таблица 9

	а	б	в	г	д	е
1	-1	-1		+1
2		+1	-1
3			+1	-1	-1
4					+1	-1

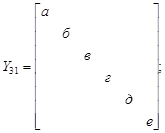
Матрица Y₃₁ при оговоренной структуре компонентных уравнений будет диагональной с размерностью, равной количеству ветвей. Для удобства обозначим 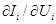именем ветви, тогда:

Покажем, что элементы матрицы Y есть не что иное, как узловые проводимости 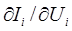. Узловой поток

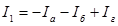
Поток в ветви считается положительным, если направлен от узла:

Предполагая, что , , , 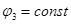получим 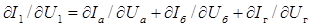, т. е. элемент y₁₁ и матрицы Y.

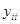Аналогично можно определить остальные элементы матрицы. Рассмотрим экономичную процедуру формирования матрицы Якоби: поочередно выбирается каждая ветвь эквивалентной схемы. Пусть очередная k-я ветвь включена между узлами с номерами i и j. Тогда проводимость этой ветви даст слагаемое в элементы матрицы и со знаком плюс, а в элементы и 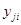- со знаком минус.

Отличительная черта узлового метода - простое формирование ММС, имеющих в своем составе многополюсные элементы. Допустим, есть элемент, включенный между тремя узлами с номерами i, j, k. Тогда этот элемент даст слагаемые в элементы матрицы Якоби:

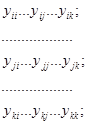
Примечание. В матрице Якоби многополюсник представлен только своими внешними узлами, в то время как может иметь и внутренние.

При применении узлового метода в эквивалентной схеме допускаются и зависимые ветви, но аргументами функциональных зависимостей должны быть только элементы вектора . Допустим, переменная типа потока в k-й ветви, включенной между узлами с номерами i и j, зависит от переменных величин типа потенциала в l-м m-м узлах:

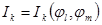Тогда эта зависимость приведет к появлению следующих элементов матрицы:

Достоинство узлового метода - простота формирования матрицы Якоби и низкий порядок получаемой системы уравнений, поскольку именно для этого метода характерно предварительное исключение большого числа неизвестных из обобщенного базиса.

Недостаток узлового метода - ограничения, накладываемые на тип используемых элементов: в узловом методе, запрещены идеальные источники переменной типа разности потенциалов, а также ветви, зависимые от переменных типа потока. Эти недостатки в узловом методе можно устранить введением специальных ветвей, которые не должны искажать физических процессов в объекте. Последовательно с идеальным источником типа разности потенциалов включается ветвь типа R, благодаря чему этот источник можно свести к источнику типа потока (рис. 8).

Рис. 8. Преобразование источника типа Е в источник типа I.

Последовательно с ветвями, потоки через которые являются управляющими, включается ветвь, у которой связь между переменными типа потока и типа разности потенциалов - линейная, т. е. ветвь типа R. Тогда зависимость от переменной типа потока через ветвь может быть заменена зависимостью от разности потенциалов на этой вспомогательной ветви.

Объясним сказанное. Пусть есть зависимый источник потока с компонентным уравнением 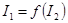, где 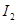- поток через управляющую ветвь, последовательно с ней включается ветвь типа R с компонентным уравнением 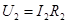тогда компонентное уравнение зависимого источника можно записать в виде .

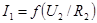Преобразования эквивалентной схемы, выполняемые для снятия ограничений в узловом методе, не всегда удобны для пользователя, более формально подобные ограничения снимаются в модифицированном узловом методе. Он получается, если базис узлового метода расширить переменными типа потока управляющих ветвей и источников типа разности потенциалов. Поскольку увеличивается количество неизвестных, соответственно должно увеличиться количество уравнений. Уравнения узлового метода дополняются компонентными уравнениями управляющих ветвей и источников типа разности потенциалов. Аддитивный вклад модели в левую и правую части системы уравнений :

Здесь 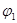и - потенциалы узлов 1 и 2, к которым подключен источник; I_Е - ток, протекающий через источник (значения I_Е определяются по результатам предыдущих итераций); - приращения соответствующих переменных.

Достоинство модифицированного узлового метода - получение ММС сравнительно невысокого порядка при практически любых зависимых ветвях, недостаток - дискретизация компонентных уравнений реактивных ветвей методами интегрирования, в результате чего смена метода интегрирования может привести к необходимости смены всех подпрограмм элементов, содержащих реактивные элементы, т. е. библиотека методов интегрирования САПР в этом случае жестко связана с библиотекой моделей элементов.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕХНИЧЕСКИХ ОБЪЕКТОВ

На сайте allrefs.net читайте: "МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕХНИЧЕСКИХ ОБЪЕКТОВ"

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Узловой метод получения математических моделей систем

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

ТЕХНИЧЕСКИХ ОБЪЕКТОВ
ВВЕДЕНИЕ. 2 1 КЛАССИФИКАЦИЯ И МЕТОДЫ ПОЛУЧЕНИЯ ММ.. 3 1.1 Классификация математических моделей. 3 1.2 Методы получения ММ... 6 1.3 Требования к м

Методы получения ММ
Основными методами получения ММ объектов на макроуровне являются: · Обобщенный метод; · Табличный метод; · Узловой метод; · Метод переменных состояний.

Требования к математическим моделям и численным методам в САПР
К математическим моделям предъявляются требования универсальности, адекватности, точности и экономичности. Степень универсальности ММ характеризует полноту отображения в модели свой

Методика получения математических моделей элементов
В общем случае процедура получения математических моделей элементов включает в себя следующие операции: 1. Выбор свойств объекта, которые подлежат отражению в модели. Этот выбор основан на

Постановка задачи
Математические модели на микроуровне, называемым распределенными, представлены дифференциальными уравнениями в частных производных вместе с краевыми условиями. Проектирование м

Краевые условия
Уравнения (1.2), (1.4), (1.6), (1.7) имеют множество решений. Для получения единственного решения необходимо задавать краевые условия (сведения об искомых непрерывных функциях на границах ра

Приближенные модели объектов на микроуровне
Точное решение краевых задач удается получить лишь для немногих частных случаев. Поэтому общий способ их решения, в том числе и в САПР, заключается в использовании различных приближенных моделей. В

Метод конечных разностей
В САПР решение дифференциальных или интегро-дифференциальных уравнений с частными производными выполняется численными методами. Эти методы основаны на дискретизации независимых переменных - их пред

Построение сетки в заданной области
В МКР пользуются, как правило, регулярные сетки, шаг которых либо постоянен, либо меняется по несложному закону. Ниже на рис. 1 приведен пример построения сеток в МКР. Для одномерных облас

Метод конечных элементов
В настоящее время метод конечных элементов (МКЭ) является одним из наиболее популярных методов решения краевых задач в САПР. В математическом отношении метод относится к группе вариационно-разностн

Метод, основанный на вариационной постановке задачи
Метод, основанный на вариационной постановке задачи, требует минимизации некоторого специально подобранного функционала, который связан с физическим смыслом задачи. Подбор функционала являет

Метод Галеркина
Метод Галеркина - другой широко известный метод вычисления вектора узловых значений - представляет собой частный случай более общего метода взвешенных невязок. Основным преимуществ

Метод граничных элементов
При решении краевых задач приближенные модели технических объектов можно строить на основе интегральных уравнений. При этом первый шаг на пути к решению состоит в переходе от дифференциальных уравн

Переход от исходного дифференциального уравнения интегральному
Рассмотрим на простом примере алгоритм перехода. В двухмерной однородной области произвольной формы с коэффициентом проницаемости k требуется найти распределение функции

Дискретизация границы рассматриваемой области
Для приближенного решения (5) производится дискретизация границы рассматриваемой области. Аналогично МКЭ разбиение границы на элементы можно производить различными способами. В простейшем случае гр

ПОСТАНОВКА ЗАДАЧИ АНАЛИЗА ОБЪЕКТОВ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
Использование ММ объекта в виде системы дифференциальных уравнений в частных производных можно только для очень простых технических систем, и даже в этом случае порядок аппроксимирующей алгебраичес

Аналогии компонентных уравнений
В большинстве технических систем можно выделить три типа простейших элементов: A. Элемент типа R - элемент диссипации энергии. На этом элементе, как правило, происходит преобразован

Электрическая подсистема
Фазовыми переменными электрической подсистемы являются токи I и напряжения U. Запишем уравнения трех типов простейших элементов: A. Уравнение сопротивления (закон Ома)

Механическая поступательная подсистема
Фазовые переменные механической поступательной подсистемы - силы F и скорости V - соответственно аналоги токов и напряжений. Запишем уравнения трех типов простейших элементов:

Механическая вращательная подсистема
Фазовые переменные этой подсистемы - моменты сил М и угловые скорости - соответ

Гидравлическая (пневматическая) подсистема
Фазовые переменные гидравлической подсистемы – массовые расходы Qm и давления Р - соответственно аналоги токов и напряжений. Запишем уравнения трех типов простейших элемент

Тепловая подсистема
Фазовые переменные этой подсистемы - тепловые потоки Ф и температура Т - соответственно аналоги токов и напряжений. Запишем уравнения трех типов простейших элементов: А. Из с

Электрическая подсистема
Связи между отдельными элементами этой подсистемы устанавливаются на основе законов Кирхгофа. Уравнение первого закона Кирхгофа устанавливает равенство нулю суммы токов в узлах схемы, т. е

Механическая поступательная подсистема
Аналогом уравнения первого закона Кирхгофа является уравнение принципа Даламбера: сумма сил, действующих на тело, включая инерционные, равна нулю, т. е.

Механическая вращательная подсистема
Аналогом уравнения первого, закона Кирхгофа является уравнение принципа Даламбера для вращательных подсистем, т. е.

Гидравлическая (пневматическая) подсистема
Аналогом уравнения первого закона Кирхгофа является уравнение равновесия в узлах подсистемы, т.е.

Тепловая подсистема
Аналогом уравнения первого закона Кирхгофа является уравнение равновесия в узлах подсистемы, т. е.

Эквивалентные схемы технических объектов
При получении ММ достаточно сложного технического объекта, состоящего из нескольких физических подсистем, нужно: 1) выделить в объекте однородные физические подсистемы, например механическ

Эквивалентные схемы механических поступательных подсистем
При построении эквивалентной схемы сначала в моделируемом объекте выделяют элементы, массу которых необходимо учесть. Такие элементы изображаются двухполюсниками (условное обозначение двухполюсника

Эквивалентные схемы гидравлических (пневматических) подсистем
За базовый узел при составлении эквивалентных схем таких подсистем обычно принимается внешняя среда. Примечание. Гидравлическая и пневматическая подсистемы аналогичны.

Эквивалентные схемы электрических подсистем
Эквивалентные схемы таких подсистем практически совпадают с их принципиальными схемами, заменяются только сложные радиокомпоненты их схемами замещения, а также могут быть учтены «паразитные» элемен

Рекомендации к составлению эквивалентных схем
При составлении эквивалентных схем следует избегать последовательного соединения источника типа I и ветви типа L, а также параллельного соединения источника типа E и ветви типа

Типы связей между подсистемами различной физической природы
Ранее были рассмотрены эквивалентные схемы однородных физических подсистем. Но реальный объект представляет собой совокупность разнородных физических подсистем. Согласно основным этапам получения М

ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
Графы в математическом обеспечении САПР используются при решении задач синтеза, особенно в конструкторском проектировании, при проектировании программного обеспечения, баз данных, при решении задач

Метод получения топологических уравнений на основе матрицы контуров и сечений
Метод, основанный на использовании информации, заключенной в М-матрице (в матрице контуров и сечений), - наиболее удобный и общий метод получения топологических уравнений.

Обобщенный метод получения математических моделей систем
Математической моделью технического объекта на макроуровне является система обыкновенных дифференциальных уравнений, в общем случае не разрешенная относительно производных, т. е.

Табличный метод получения математических моделей систем
В табличном методе в вектор базисных координат включаются переменные величины типа U и I для всех ветвей схемы. Выбор такого базиса позволяет в эквивалентной схеме иметь любые зависимые ветв

Метод переменных состояния
Базис метода переменных, характеризующих состояние системы, или более коротко - метода переменных состояния, составляют переменные типа потока через элементы типа

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ТЕХНИЧЕСКИХ ОБЪЕКТОВ ДЛЯ ПОЛУЧЕНИЯ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
Для многих технических объектов, описываемых системой линейных дифференциальных уравнений, необходимо получение амплитудно-частотных и фазочастотных характеристик (АЧФ и ФЧХ). Часто АЧХ и ФЧХ опред

Численный метод анализа частотных характеристик
Поскольку модель технического объекта предполагается линейной, целесообразно записать ее относительно приращений:

Метод полиномиальных коэффициентов
Так как математическая модель объекта линейна, то , где

Символический метод
Здесь большая часть действий по определению коэффициентов аi и bj производится в общем виде, т. е. выполняются операции над символическими обозначениями, в резул

МЕТОДЫ АНАЛИЗА ПОВЫШЕННОЙ ЭФФЕКТИВНОСТИ
Одновариантный анализ служит для оценки выходных параметров объектов при заданных внутренних и внешних параметрах. Он является необходимой составной частью более сложных задач много

Диакоптические методы анализа
Диакоптические методы (методы разбиения, декомпозиции) основаны на разделении сложной системы уравнений высокой размерности на более простые подсистемы с учетом связей между ними. В результа