Воздействие скачка постоянного напряжения на последовательный колебательный контур

Несколько усложним задачу, рассмотрев воздействие скачка постоянного напряжения на последовательный колебательный контур (рис. 6.5).

 

 

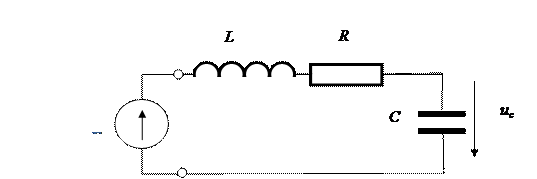Рис. 6.5. Воздействие скачка постоянного напряжения на последовательный колебательный контур

 

На основании второго закона Кирхгофа можно записать уравнение для напряжений в контуре

.

 

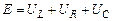Если напряжения на зажимах элементов выразим через ток в контуре, то получим следующее интегро-дифференциальное уравнение

 

,

 

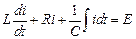Введя интеграл с переменным верхним пределом, найдем

 

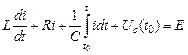. (6.15)

где t₀ - время, принятое за начало отсчета;

U_c(t₀) - значение напряжение на емкости при t=t₀.

Если при t = 0 напряжение на емкости равно нулю, то последнее уравнение можно записать в виде

 

.

 

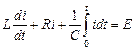Выразим значение тока через

 

.

 

Подставив это выражение в предыдущее уравнение, после несложных преобразований получим

 

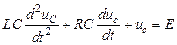(6.16)

 

Уравнение (6.16) -неоднородное линейное дифференциальное уравнение второго порядка.

Соответствующее ему однородное уравнение имеет вид

. (6.17)

 

Уравнение (6.17) определяет свободные колебания в цепи RLC.

Эйлер, основываясь на свойстве пропорциональности экспоненты своим производным, предложил искать решение уравнения (6.17) в виде

 

,

 

где p - некоторая постоянная, которую нужно определить. Так как при таком выборе

 

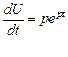и ,

то после подстановки производных в (6.17) получим характеристическое уравнение

 

или

 

Корни характеристического уравнения определяются как

.

Введем общепринятые обозначения для коэффициента затухания

 

и круговой резонансной частоты

 

Тогда выражение для корней характеристического уравнения будет выглядеть следующим образом

 

,

или

 

. (6.18)

 

Введем обозначение

 

где ω₁ - круговая частота собственных затухающих колебаний контура RLC.

Теперь корни характеристического уравнения можно представить в виде пары сопряженных комплексных чисел

 

.

 

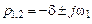Известно, что общее решение однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами находится в виде

 

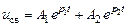. (6.19)

 

Решение этого уравнения получается в результате двух интегрирований и, поэтому, оно содержит две произвольные постоянные A₁ и A₂.

Результирующее напряжение на емкости будет выглядеть как

 

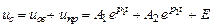. (6.20)

 

Константы A₁ и A₂ находятся из начальных условий. Предположим, что в момент времени t = 0 емкость С была разряжена и ток в контуре был равен нулю.

При подключении к контуру скачка напряжения напряжение на емкости не может измениться скачком (первый закон коммутации), то есть

 

U_с(0) = 0

 

Ток через индуктивность также не может измениться скачком вследствие того же закона коммутации

 

i(0) = 0.

 

Поэтому

 

.

 

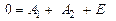Ток в контуре может быть определен как

 

.

 

Взяв производную от выражения (6.20) и приравняв ее нулю, получим

 

. (6.21)

 

Для момента времени t = 0 получим

 

.

 

Таким образом, для указанных начальных условий имеем систему двух линейных уравнений с двумя неизвестными

 

,

.

 

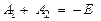Соответствующие постоянные интегрирования равны

 

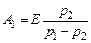и .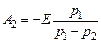

 

Поскольку

,

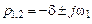то

и .

 

После подстановки в (6.19) корней характеристического уравнения и постоянных интегрирования имеем

 

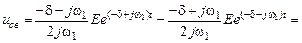
. (6.22)

 

С учетом формул Эйлера

 

, ,

 

получим

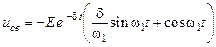. (6.23)

 

Воспользовавшись известным тригонометрическим соотношением

 

где

и .

 

уравнение (6.23) можно записать в виде

 

,

где .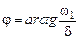

Напомним, что общее решение неоднородного дифференциального уравнения является суммой принужденной и свободной составляющей. Следовательно, выходное напряжение после подключения постоянного напряжения к контуру RLC (при комплексных корнях характеристического уравнения) будет определяться как

 

. (6.24)

 

Выражение (6.24) показывает, что при подключении к цепи RLC постоянного напряжения в ней возникают затухающие гармонические колебания. Природа колебаний объясняется периодическим преобразованием энергии электрического поля емкости С в энергию магнитного поля индуктивности L и обратно, причем эта энергия постепенно рассеивается на сопротивлении R

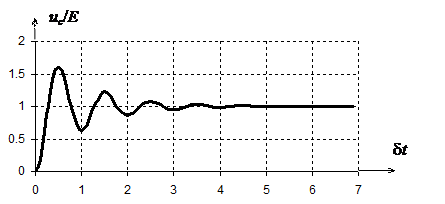На рис. 6.6 представлен график изменения напряжения во времени, построенный в соответствии с выражением (6.24).

Рис.6.6. Напряжение на емкости последовательного колебательного контура при подаче на его вход скачка постоянного напряжения

 

В случае, когда коэффициент затухания δ равен нулю, корни характеристического уравнения становятся чисто мнимыми 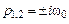, а угол φ равен π/2 . При этом свободные колебания становятся незатухающими, и частота их равна ω₀

.

 

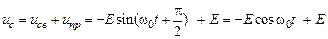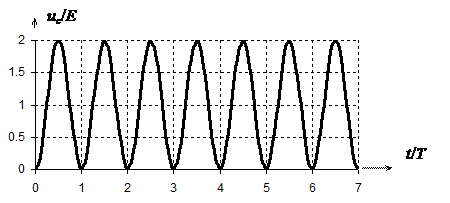Соответствующий график показан на рис. 6.7.

 

Рис.6.7. Напряжение на емкости последовательного колебательного контура при подаче на его вход скачка постоянного напряжения в при d = 0

 

Отметим , что представленный случай является теоретическим, так как на самом деле не существует реальных контуров без потерь и поэтому колебания неизбежно затухают.

Заметим также, что при подключении постоянного напряжения к контуру RLC выброс (см. рис.6.6) не может превышать удвоенного значения напряжения.

Рассмотрим случай действительных корней. Как следует из (6.18)

 

для .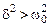

 

С учетом начальных условий уравнение свободных колебаний будет выглядеть следующим образом

.

 

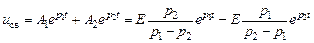Тогда результирующее напряжение на емкости после подключения постоянного напряжения величиной Е будет равно

 

.

 

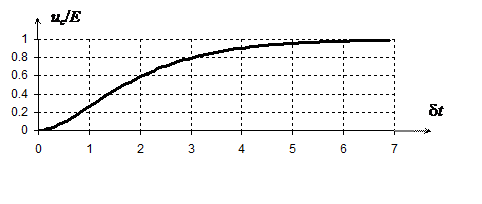На рис.6.8 показан график напряжения, построенный для значений корней p ₁= -0,9δ и p₂ = -1,1δ .

Рис. 6.8. Напряжение на емкости последовательного колебательного контура при подаче на его вход скачка постоянного напряжения в случае действительных корней характеристического уравнения

 

Обратим внимание, что при действительных корнях отсутствует колебательный процесс. Этого следовало ожидать, так как, график определяется суммой постоянного напряжения и двух экспоненциальных функций.

Cлучай равных и действительных корней

 

для

 

может рассматриваться как предельный случай апериодического режима.

Положив в (6.23) , ω₁ → 0 и приняв во внимание что , получим выражение для свободной составляющей:

 

 

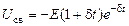
Соответственно, уравнение напряжения на емкости при подключении постоянного напряжения к контуру

 

.

 

Как и в рассмотренном выше случае, переходный процесс носит тот же апериодический характер . Характер переходного процесса тот же, что и на рис. 6.8

Итак, по корням характеристического уравнения RLC - цепи можно судить о характере переходного процесса:

если корни характеристического уравнения образуют пару сопряженных комплексных чисел, вещественные части которых отрицательны, то свободные колебания носят затухающий характер;

при мнимых корнях колебания не затухают и их амплитуда равна Е (теоретический случай);

для отрицательных действительных и разных корней, а также для равных кратных отрицательных корней процесс носит апериодический характер.