Програмна реалізація основних елементів ШПФ - раздел Связь, Тема 1: Вступ до дисципліни Проектування цифрової обробки сигналів та зображень. Основні поняття та визначення 1. Області застосування та основні задачі цифрової обробки сигналів Алгоритм Попередньої Перестановки
Розглянемо Конкретну Реаліз...
Алгоритм попередньої перестановки
Розглянемо конкретну реалізацію ШПФ. Нехай є N=2T елементів послідовності x{N} і треба одержати послідовність X{N}. Розділимо x{N} на дві послідовності: парні і непарні елементи і т.д з кожною послідовністю. Ітераційний процес закінчиться, коли залишаться послідовності довжиною по 2 елементи. Приклад процесу для N=16 показаний нижче:

Разом виконується (log2N)-1 ітерацій.
Розглянемо двійкове представлення номерів елементів і займаних ними місць. Елемент із номером 0 (0000) після всіх перестановок займає позицію 0 (0000), елемент 8 (1000) - позицію 1 (0001), елемент 4 (0100) - позицію 2 (0010), елемент 12 (1100) - позицію 3 (0011). І так далі. Позиції до і після перестановок дзеркально симетричні. Двійкове представлення кінцевої позиції виходить із двійкового представлення початкової позиції перестановкою бітів у зворотному порядку. І навпаки.
Це є закономірним для всіх N. На першому кроці парні елементи з номером n перемістилися в позицію n/2, а непарні з позиції в позицію N/2+(n-1)/2, де n=0,1,..., N-1. Таким чином, нова позиція обчислюється зі старої позиції як:
ror(n,N) = [n/2] + N{n/2},
де [x] - ціла частина числа, {x} - дробова.
В асемблері ця операція - циклічний зсув вправо (ror), якщо N - ступінь двійки. Спочатку береться двійкове представлення числа n, потім всі біти, крім молодшого зміщуються на 1 позицію вправо, а молодший біт переміщається на місце, що звільнилося, найстаршого (лівого) біта (див. рис.2.2).
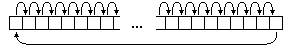
Рис. 2.2
Подальші розбиття виконуються аналогічно. На кожному наступному кроці кількість послідовностей подвоюється, а число елементів у кожній з них зменшується вдвічі. Операції ror піддаються вже не всі біти, а тільки кілька молодших. Старші j-1 бітів залишаються недоторканими (зафіксованими), де j - номер кроку (див. рис.2.3):

Рис. 2.3
Простежимо за довільним бітом номера позиції. Нехай біт перебував в j-му двійковому розряді. Біт буде послідовно зсуватися вправо на кожному кроці доти, поки не виявиться в крайній правій позиції (після j-го кроку). На j+ 1-му кроці буде зафіксовано j старших бітів, а той біт, за яким стежимо, переміститься в розряд з номером T-j-1, що і необхідно для дзеркальної перестановки біт.
Алгоритм перестановки бітів наведений нижче:
for(I = 1; I < N-1; I++)
{
J = reverse(I,T); //reverse переставляє біти в I у зворотному порядку
if (I >= J) // пропустити вже переставлені
conitnue;
S = x[I]; x[I] = x[J]; x[J] = S; // перестановка елементів xI і xJ
}
Операція зворотної перестановки біт може бути реалізована через інші бітові операції. Нижче наведений алгоритм функції перестановки T молодших бітів у числі I:
unsigned int reverse(unsigned int I, int T)
{
int Shift = T - 1;
unsigned int LowMask = 1;
unsigned int HighMask = 1 << Shift;
unsigned int R;
for(R = 0; Shift >= 0; LowMask <<= 1, HighMask >>= 1, Shift -= 2)
R |= ((I & LowMask) << Shift) | ((I & HighMask) >> Shift);
return R;
}
У змінних LowMask і HighMask зберігаються маски, що виділяють два біти, які переставляються. Перша маска у двійковому поданні виглядає як 0000...001 і в циклі змінюється, зсуваючи одиницю щораз на 1 розряд вліво:
0000...001
0000...010
0000...100
...
Маска HighMask за кожну ітерацію зсуває одиничний біт на 1 розряд вправо.
1000...000
0100...000
0010...000
...
Ці зсуви виконуються інструкціями LowMask <<= 1 і HighMask >>= 1.
Змінна Shift показує відстань (у розрядах) між бітами, що переставляються. Спочатку вона дорівнює T-1 і кожну ітерацію зменшується на 2. Цикл припиняється, коли відстань стає менше або дорівнює нулю.
Операція I & LowMask виділяє перший біт, потім він зсувається на місце другого (<<Shift). Операція I & HighMask виділяє другий біт, потім він зсувається на місце першого (>>Shift). Після чого обидва біти записуються в змінну R операцією "|".
Замість того щоб переставляти біти позицій місцями, можна застосувати і інший метод. Для цього треба вести відлік 0,1,2,...,N/ 2-1 уже зі зворотним проходженням бітів. Алгоритм збільшення на одиницю можна реалізувати програмно, приклад для T=4 наведений нижче.
I = 0;
J = 0;
for(J1 = 0; J1 < 2; J4++, J ^=1)
for(J2 = 0; J2 < 2; J3++, J ^=2)
for(J4 = 0; J4 < 2; J4++, J ^=4)
for(J8 = 0; J8 < 2; J8++, J ^=8)
{
if (I < J)
{
S = x[I]; x[I] = x[J]; x[J] = S; // перестановка елементів xI і xJ
}
I++;
}
У алгоритмі враховано, що при збільшенні числа від 0 до нескінченності (зі збільшенням на одиницю) кожний біт міняється з 0 на 1 і назад з певною періодичністю: молодший біт - щораз, наступний - кожний другий раз, наступний - кожний четвертий і так далі. Ця періодичність реалізована у вигляді T вкладених циклів, у кожному з яких один з бітів позиції J перемикається туди і назад за допомогою операції XOR (В C/C++ записується як ^=). Позиція I використовує звичайний інкремент I++.
Даний алгоритм залежить від кількості вкладених циклів залежно від T. Оскільки T звичайно обмежено деякою розумною межею (16..20), то можна написати декілька варіантів алгоритму. Нижче наведений варіант цього алгоритму, що емулює вкладені цикли через стеки Index і Mask.
int Index[MAX_T];
int Mask[MAX_T];
int R;
for(I = 0; I < T; I++)
{
Index[I] = 0;
Mask[I] = 1 << (T - I - 1);
}
J = 0;
for(I = 0; I < N; I++)
{
if (I < J)
{
S = x[I]; x[I] = x[J]; x[J] = S; // перестановка елементів xI і xJ
}
for(R = 0; R < T; R++)
{
J ^= Mask[R];
if (Index[R] ^= 1) // еквівалентно Index[R]^=1; if (Index[R] != 0)
break;
}
}
Величина MAX_T визначає максимальне значення для T і в найгіршому випадку дорівнює розрядності цілочисельних змінних. Даний алгоритм повільнішим від попереднього, але економніший за обсягом коду.
І ще один алгоритм, який використовує класичний підхід до багаторозрядних бітових операцій: треба розділити 32-біта на 4 байти, виконати перестановку в кожному з них, після чого переставити самі байти.
Перестановку бітів в одному байті можна робити по таблиці, для якої потрібно мати масив reverse256 з 256 елементів (записані числа від 0 до 255 з переставленими в кожному порядок бітів).
Даний масив можна застосувати для реалізації функції reverse:
unsigned int reverse(unsigned int I, int T}
{
unsigned int R;
unsigned char *Ic = (unsigned char*) &I;
unsigned char *Rc = (unsigned char*) &R;
Rc[0] = reverse256[Ic[3]];
Rc[1] = reverse256[Ic[2]];
Rc[2] = reverse256[Ic[1]];
Rc[3] = reverse256[Ic[0]];
R >>= (32 - T);
Return R;
}
Звертання до масиву reverse256 переставляють у зворотному порядку біти в кожному байті. Покажчики Ic і Ir дозволяють звернутися до окремих байтів 32-бітних чисел I і R і переставити у зворотному порядку байти. Зсув числа R вправо наприкінці алгоритму усуває розходження між перестановкою 32 біт і перестановкою T біт. Геометрична ілюстрація алгоритму, де стрілками показані перестановки бітів, байтів і зсув наведена на рис.2.4.
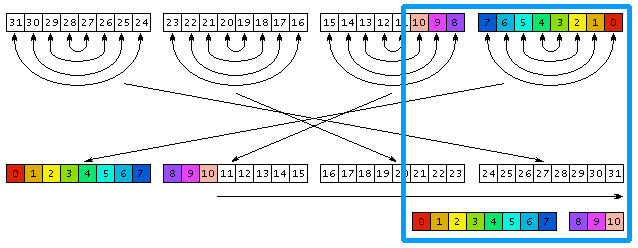 Рис. 2.4
Рис. 2.4
У всіх випадках є N перестановок з порівнянням I і J, що запобігає повторній перестановці деяких елементів.
Перевагу необхідно надати останньому алгоритму - він має усього N переходів.
Оптимізований останній алгоритм наведено нижче.
static unsigned char reverse256[]=
{
0x00, 0x80, 0x40, 0xС0, 0x20, 0xA0, 0x60, 0xE0,
0x10, 0x90, 0x50, 0xD0, 0x30, 0xB0, 0x70, 0xF0,
0x08, 0x88, 0x48, 0xC8, 0x28, 0xA8, 0x68, 0xE8,
0x18, 0x98, 0x58, 0xD8, 0x38, 0xB8, 0x78, 0xF8,
0x04, 0x84, 0x44, 0xC4, 0x24, 0xA4, 0x64, 0xE4,
0x14, 0x94, 0x54, 0xD4, 0x34, 0xB4, 0x74, 0xF4,
0x0C, 0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC,
0x1C, 0x9C, 0x5C, 0xDC, 0x3C, 0xBC, 0x7C, 0xFC,
0x02, 0x82, 0x42, 0xC2, 0x22, 0xA2, 0x62, 0xE2,
0x12, 0x92, 0x52, 0xD2, 0x32, 0xB2, 0x72, 0xF2,
0x0A, 0x8A, 0x4A, 0xCA, 0x2A, 0xAA, 0x6A, 0xEA,
0x1A, 0x9A, 0x5A, 0xDA, 0x3A, 0xBA, 0x7A, 0xFA,
0x06, 0x86, 0x46, 0xC6, 0x26, 0xA6, 0x66, 0xE6,
0x16, 0x96, 0x56, 0xD6, 0x36, 0xB6, 0x76, 0xF6,
0x0E, 0x8E, 0x4E, 0xCE, 0x2E, 0xAE, 0x6E, 0xEE,
0x1E, 0x9E, 0x5E, 0xDE, 0x3E, 0xBE, 0x7E, 0xFE,
0x01, 0x81, 0x41, 0xC1, 0x21, 0xA1, 0x61, 0xE1,
0x11, 0x91, 0x51, 0xD1, 0x31, 0xB1, 0x71, 0xF1,
0x09, 0x89, 0x49, 0xC9, 0x29, 0xA9, 0x69, 0xE9,
0x19, 0x99, 0x59, 0xD9, 0x39, 0xB9, 0x79, 0xF9,
0x05, 0x85, 0x45, 0xC5, 0x25, 0xA5, 0x65, 0xE5,
0x15, 0x95, 0x55, 0xD5, 0x35, 0xB5, 0x75, 0xF5,
0x0D, 0x8D, 0x4D, 0xCD, 0x2D, 0xAD, 0x6D, 0Xed,
0x1D, 0x9D, 0x5D, 0xDD, 0x3D, 0xBD, 0x7D, 0xFD,
0x03, 0x83, 0x43, 0xC3, 0x23, 0xA3, 0x63, 0xE3,
0x13, 0x93, 0x53, 0xD3, 0x33, 0xB3, 0x73, 0xF3,
0x0B, 0x8B, 0x4B, 0xCB, 0x2B, 0xAB, 0x6B, 0xEB,
0x1B, 0x9B, 0x5B, 0xDB, 0x3B, 0xBB, 0x7B, 0xFB,
0x07, 0x87, 0x47, 0xC7, 0x27, 0xA7, 0x67, 0xE7,
0x17, 0x97, 0x57, 0xD7, 0x37, 0xB7, 0x77, 0xF7,
0x0F, 0x8F, 0x4F, 0xCF, 0x2F, 0xAF, 0x6F, 0xEF,
0x1F, 0x9F, 0x5F, 0xDF, 0x3F, 0xBF, 0x7F, 0xFF,
}
unsigned int I, J;
unsigned char *Ic = (unsigned char*) &I;
unsigned char *Jc = (unsigned char*) &J;
for(I = 1; I < N - 1; I++)
{
Jc[0] = reverse256[Ic[3]];
Jc[1] = reverse256[Ic[2]];
Jc[2] = reverse256[Ic[1]];
Jc[3] = reverse256[Ic[0]];
J >>= (32 - T);
if (I < J)
{
S = x[I];
x[I] = x[J];
x[J] = S;
}
}
Основний цикл алгоритму
На рис.2.5 наведений другий етап обчислення ДПФ. Лініями зверху вниз показано використання елементів для обчислення значень нових елементів. Зручно, що два елементи на певних позиціях в масиві дають два елементи на тих самих місцях. Тільки належати вони будуть вже іншим, більш довшим масивам, що розміщені на місці попередніх (коротших). Це дозволяє обійтись одним масивом даних для вихідних даних, результату і зберігання проміжних результатів для всіх T ітерацій.

Рис. 2.5
Нижче наведені дії, які необхідно виконати після первинної перестановки елементів.
#define T 4
#define Nmax (2 << T)
complex Q, Temp, j(0,1);
static complex x[Nmax];
static double pi2 = 2 * 3.1415926535897932384626433832795;
int N, Nd2, k, mpNd2, m;
for(N = 2, Nd2 = 1; N <= Nmax; Nd2 = N, N += N)
{
for(k = 0; k < Nd2; k++)
{
W = exp(-j*pi2*k/N);
for(m = k; m < Nmax; m += N)
{
mpNd2 = m + Nd2;
Temp = W * x[mpNd2];
x[mpNd2] = x[m] - Temp;
x[m] = x[m] + Temp;
}
}
}
Змінна Nmax містить повну довжину масиву даних і кінцеву кількість елементів ДПФ. В таблиці наведена відповідність між виразами в формулі (2.9) і змінними в програмі.
| В алгоритмі
| В формулі
|
| N
| N
|
| Nd2
| N/2
|
| k
| K
|
| m
| k з поправкою на номер послідовності
|
| mpNd2
| k+N/2 з поправкою на номер послідовності
|
| pi2
| 2π
|
| j
| j (уявна одиниця)
|
| x[k] (на початку циклу)
| X{N/2}[even]k
|
| x[mpNd2] (на початку циклу)
| X{N/2}[odd]k
|
| x[k] (в кінці циклу)
| X{N}k
|
| x[mpNd2] (в кінці циклу)
| X{N}N/2+k
|
| W
| 
|
Зовнішній цикл - це основні ітерації. На кожній из них 2Nmax/N ДПФ (довжиною по N/2 елементів кожне) перетворюється в Nmax/N ДПФ (довжиною по N елементів кожне).
Наступний цикл по k є циклом синхронного обчислення елементів з індексами k і k + N/2 у всіх результуючих ДПФ.
Внутрішній цикл перебирає Nmax/N штук ДПФ одне за другим: спочатку обчислюються елементы з номерами 0 и N/2, у всіх ДПФ в кількості Nmax/N штук, потім з номерами 1 і N/2 + 1 і т.д. На рис.2.5 показана послідовність обчислень для N = 8, в якій забезпечується однократне обчислення  .
.
x[mpNd2] обчислюється раніше від x[k], щоб x[k] не було модифіковано перед використанням.
Алгоритм оберненого ДПФ відрізняється тим, що замість -j треба використовувати +j і після всіх обчислень поділити кожне x[k] на Nmax.
Оптимізація повертаючих множників
Для обчислення повертаючих множників можна використати формулу (10), що дозволить
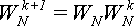 . (2.10)
. (2.10)
уникнути операцій піднесення до ступеня і обійтися одними множеннями, якщо заздалегідь обчислити WN для N = 2, 4, 8,…,Nmax. У міру збільшення k повертаючий множник буде змінюватися, але разом з тим буде рости похибка обчислень. І після N/2 підряд множень у повертаючому множнику, може нагромадитися велике відхилення від точного значення, оскільки при множенні величин їхні відносні похибки сумуються.
Цього можна було б уникнути, будь число WN цілим, але воно не ціле при N > 2, тому що обчислюється через значення синуса і косинуса:
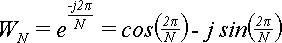
Уникнути багатьох звертань до повільних функцій синуса і косинуса можна за допомогою алгоритму обчислення ступеня через багаторазові піднесення до квадрату і множення. Наприклад:

У цьому випадку необхідно всього 5 множень ( не потрібно обчислювати двічі) замість 13. У найгіршому випадку для піднесення до ступеня від 1 до N/ 2-1 потрібно log2N множень замість N/2, що дає цілком прийнятну похибку для більшості практичних задач.
не потрібно обчислювати двічі) замість 13. У найгіршому випадку для піднесення до ступеня від 1 до N/ 2-1 потрібно log2N множень замість N/2, що дає цілком прийнятну похибку для більшості практичних задач.
Можна вдвічі зменшити кількість множень на кожному кроці, якщо використовувати результати минулих обчислень
 ,
,
для зберігання яких потрібно додатково log2(Nmax) комплексних комірок пам'яті:
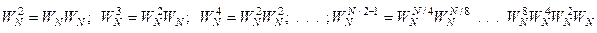
Якщо чергове  не було обчислено попередньо, то береться двійкове представлення k і аналізується. Кожному одиничному біту відповідає рівно один множник. У загальному випадку одиниці в біті з номером b відповідає множник
не було обчислено попередньо, то береться двійкове представлення k і аналізується. Кожному одиничному біту відповідає рівно один множник. У загальному випадку одиниці в біті з номером b відповідає множник  , що зберігається в b-ій комірці масиву.
, що зберігається в b-ій комірці масиву.
Для зменшення кількості множень при обчисленні  до одного на два цикли необхідно відвести N/2 комплексних комірок для зберігання всіх попередніх
до одного на два цикли необхідно відвести N/2 комплексних комірок для зберігання всіх попередніх  . Непарні елементи обчислюються за формулою (2.10). Парні обчислюються за формулою
. Непарні елементи обчислюються за формулою (2.10). Парні обчислюються за формулою 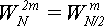 , тобто, нічого не обчислюється, а береться одне зі значень, обчислених на попередньому кроці, коли N було вдвічі менше. Щоб не потрібно було копіювати величини на нові позиції досить їх відразу розташовувати в тій позиції, що вони займуть при N = Nmax і вводити просте виправлення Skew.
, тобто, нічого не обчислюється, а береться одне зі значень, обчислених на попередньому кроці, коли N було вдвічі менше. Щоб не потрібно було копіювати величини на нові позиції досить їх відразу розташовувати в тій позиції, що вони займуть при N = Nmax і вводити просте виправлення Skew.
Пояснення до лістингу, що наведений нижче.
1. Реалізовані найпростіші операції над комплексними числами (класи Complex і ShortComplex), оптимізовані під дану задачу.
2. Масив W2n містить заздалегідь обчислені коефіцієнти W2, W4, W8,...,WNmax.
3. Для обчислень використовуються найточніші представлення чисел із плаваючою крапкою в C++: long double розміром в 10 байт. Для зберігання результатів у масивах використовується тип double довжиною 8 байт.
/*
Fast Fourier Transformation
====================================================
*/
#ifndef FFT_H_
#define FFT_H_
struct Complex;
struct ShortComplex;
/*
Fast Fourier Transformation: direct (complement= false)
and complement (complement = true). 'x' is data source.
'x' contains 2^T items.
*/
extern void fft(ShortComplex *x, int T, bool complement);
struct ShortComplex
{
double re, im;
inline void operator=(const Complex &y);
};
struct Complex
{
long double re, im;
inline void operator= (const Complex &y);
inline void operator= (const ShortComplex &y);
};
inline void ShortComplex::operator=(const Complex &y) { re = (double)y.re; im = (double)y.im; }
inline void Complex::operator= (const Complex &y) { re = y.re; im = y.im};
inline void Complex::operator= (const ShortComplex &y) { re = y.re; im = y.im};
#endif
Все темы данного раздела:
Основні поняття та визначення. Основні характеристики сигналів
Сигнал (в теории информации и связи) — материальный носитель информации, используемый для передачи сообщений в системе связи. Сигналом может быть люб
Природа сигналів. За своєю природою, сигнали можуть бути випадкові або детерміновані.
До детермінованих відносять сигнали, значення яких у будь-який момент часу або в довільній точці простору є апріорно відомими або можуть бути досить точно визначені (обчислені) за відомою чи передб
Аналогові та цифрові сигнали.
До основних типів відносять аналоговий, дискретний і цифровий сигнали.
Аналоговим називають сигнал, неперервний у часі і значеннях. Такий сигнал описується неперервною або кусочно н
Основні типи сигналів
Фінітні сигнали. Фінітним називається сигнал, який визначений лише на деякому часовому проміжку і не існує поза ним, тобто при t>T, амплітуда сигналу рівна нулю.
Пер
Елементарні сигнали, що найчастіше використовуються ЦОС
Всі сигнали ми будемо розглядати в аналоговому та неперервному варіантах.
1. Неперервний випадок
Властивості спектрів дискретних сигналів
1. Неперервність.
2. Періодичність..
3. Спектр дійсного сигналу. Якщо - д
Режим реального часу
Основними прикладними (інженерними, практичними) задачами обробки сигналів є:
1. Ідентифікація і розпізнавання.
2. Телекомунікації.
3. Обробка музичних і мо
Переваги і недоліки ЦОС
Перевагами ЦОС є:
Гарантована точність
Цілковита відтворюваність. Можна ідентично відтворити кожний елемент, оскільки відсутні відхилення, обумовлен
Основні операції цифрової обробки сигналів
Проте всі ці алгоритми, як правило - блокового типу, тобто побудовані на як завгодно складних комбінаціях досить невеликого набору типових цифрових операцій, до основного з яких відносяться: зго
Застосування ДПФ
На рис. 5.1 наведена схема взаємодії між часовою та частотною областями.
Основними сферами застосування ДПФ є:
- цифровий спектральний аналіз - аналізатори спектра, обробка мови,
ДПФ як згортка сигналу з базисними функціями
Оскільки комплексна експонента може бути представлена у виді дійсної та уявної частини (формула Ейлера), то основне рівняння ДПФ може бути записано таким чином:
Основні операції фільтрації
До основних операцій фільтрації інформації відносять:
- згладжування;
- прогнозування;
- диференціювання;
- інтегрування;
- поділ на певні складові;
Класи і параметри фільтрів
Залежно від призначення фільтру, а отже і загального виду його частотної характеристики, виділяють такі основні, найбільш розповсюджені, типи фільтрів (вибіркові фільтри):
-
Поняття про швидкі алгоритми
При побудові швидких алгоритмів використовують кілька основних прийомів. Серед них найголовнішими є :
1. Розбиття задачі на підзадачі.
2. Рекурсія - коли деякий метод чи прийом мо
Вправи і завдання до теми №1
1. Визначити період заданого сигналу: .
Відповідь :
Зменшення частоти дискретизації: децимація із цілим кроком
На рис. 1.1, а наведена блок-схема процесу децимації сигналу х(n) із цілим кроком М. На ній зображені цифровий фільтр захисту від накладення спектрів h(k) і схема стиску (компресор) частоти дискрет
Збільшення частоти дискретизації: інтерполяція із цілим кроком
Інтерполяція - це цифровий еквівалент процесу цифроаналогового перетворення, коли із цифрових вибірок, поданих на цифроаналоговий перетворювач, за допомогою інтерполяції відновлюється аналоговий си
Перетворення частоти дискретизації з нецілим кроком
У деяких ситуаціях часто буває потрібно змінити частоту дискретизації в неціле число раз. Приклад - цифрове аудіо, де може вимагатися передача даних з одного запам'ятовувального пристрою на інше, п
Багатокаскадне перетворення частоти дискретизації
У п.1.3 зміна частоти дискретизації відбувалося відразу з використанням єдиного коефіцієнта децимації або інтерполяції. Якщо потрібне значна зміна частоти дискретизації, такий підхід неефективний;
Розробка практичних конвертерів частоти дискретизації
Розробку практичного багатокаскадного конвертера частоти дискретизації можна розбити на чотири етапи:
Задати загальні вимоги до фільтрів захисту від накладення спектрів і придушення
Специфікація фільтру
Фактично продуктивність системи обробки при декількох швидкостях критично залежить від типу НІХ
і якості використовуваного фільтра. Відзначимо, що при децимації й інтерполяції можуть викор
Високоякісне аналого-цифрове перетворення в цифровому аудіо
У сфері цифрового аудіо постійно потрібно підвищувати якість, дозвіл і швидкість АЦП. Це привело до розробки однобітових АЦП із використанням методів дельта-сігма-модуляції. У результаті з'явилася
Ефективне аналого-цифрове перетворення у високоякісних системах відтворення компакт-дисків
Одним з перших серйозних застосувань методів з обробкою при декількох швидкостях стало відтворення звуку й музики в програвачах компакт-дисків.
На рис. 6.2 зображена схема відновлення анал
Особливості діагностики та контролю процесорів та систем опрацювання сигналів та зображень
Для контролю і діагностики вузлів опрацювання сигналів застосовуються різні сполучення відомих методів вбудованого і зовнішнього контролю ЕОМ, або методи діагностики складних систем, що базуються н
Рархічність засобів діагностики та контролю процесорів та систем опрацювання сигналів та зображень
Ієрархічність засобів діагностики відповідає ієрархічності обчислювальних засобів. Тому розглядається ієрархічність на рівні: систем, процесорів та окремих вузлів.
Використовуються такі за
Процес формування АЧХ
Для обчислення АЧХ нерекурсивних ЦФ здебільшого застосовують метод передаточних функцій. Від передаточної функції, яка в загальному вигляді записується як многочлен виду:
H(Z)= a
Визначення і дослідження виду АЧХ
Нехай задано проаналізувати АЧХ фільтра з такими параметрами сигналу: l = 0,1, ...,31; А = 1, 2,...,100; S = 8, 16; Q = -64...64; N = 0,1, …, 31.
Згідно
Структура потокового (ковзаючого) процесора ШПФ.
6.Методика вибору оптимального складу НВІС
Розглядаються передумови і методика однокристальної реалізації швидкого перетворення Фур'є на приладах програмувальної логіки фі
Використання ПЛІС для високопродуктивної цифрової обробки сигналів та зображень
Є ряд альтернативних рішень побудови високопродуктивних систем, зокрема на замовлених інтегральних схемах (ASІ) і спеціалізованих процесорах цифрової обробки сигналів (DSP). Розглядати питання реал
Таблиця 1. Основні характеристики ПЛІС Xіlіnx серій Vіrtex, Vіrtex-e, XC4000XL/XLAXV, Spartan/XL
Сімейство ПЛІС
Системна частота, МГЦ
Швидкодія, нс/вентиль
Швидкість обміну chіp-to-chіp, МГЦ
Ємність ПЛІС, системних вентилів
Таблиця 1. Основні характеристики ПЛІС Xіlіnx серій Vіrtex, Vіrtex-e, XC4000XL/XLAXV, Spartan/XL
Сімейство ПЛІС
Системна частота, МГЦ
Швидкодія, нс/вентиль
Швидкість обміну chіp-to-chіp, МГЦ
Ємність ПЛІС, системних вентилів
Оцінка продуктивності вузла виконання операцій ШПФ на ПЛІС.
Оцінимо необхідну продуктивність пристрою обробки. Для обчислення ШПФ 256 точок за основою 2 з комплексними вхідними даними потрібно приблизно 3 тис. множень дійсних операндів і 5,5 тис. додавань д
Таблиця 1. Характеристики М-модулів ШПФ на ПЛІС серії Vіrtex
Розмір перетворення
Системних вентилів, тис.
Частота надходження вхідних даних, Мгц-real-tіme
Час перетворення, мкс
Структура потокового (ковзаючого) процесора ШПФ.
У загальному випадку при побудові М-модуля ШПФ можна піти декількома шляхами: або спроектувати модулі з малими займаними обсягами, великим часом перетворення і малою швидкістю надходження вхідних д
Таблиця 2. Характеристики М-модулів ковзного ШПФ на ПЛІС Xіlіnx
Число точок
Тактова частота, МГц
Час перетворення, мкс
Об’єм модуля, логічних комірок
Необхідна ПЛІС
Визначення нейрокомп’ютера.
Нейрокомпьютери - дуже модне слово, яке використовують направо і наліво. На початку 90-х років був дуже бурхливий розвиток даної тематики у вітчизняних розробках. Але разом з рядом серйозних розроб
Базова структура нейрокомп’ютера на основі ПОС.
Зупинимося на особливостях апаратної реалізації нейрообчислювача (НО) (див. рис.5) з можливістю паралельної обробки, що реалізують елементи нейромережі.
Порівняльні характеристики нейрокомп’ютерів на базі ПОС.
Для побудови НО (нейрообчислювач) перспективним є використання сигнальних процесорів із плаваючою крапкою ADSP2106x, TMS320C4x,8x, DSP96002 і ін. Типова структурна схема реалізації НО на основі сиг
Реалізація ШПФ на нейрокомп’ютері.
Розглянемо реалізацію ШПФ на базі процесора Л1879ВМ1(NM6403). Процесор Л1879ВМ1 - високопродуктивний спеціалізований мікропроцесор, що об’єднює в собі риси двох сучасних архітектур: VLIW (Very Long
Співпроцесора NM6403 при розбитті матриці співпроцесора NM6403 при розбитті матриці
вагових коефіцієнтів - (2х32біти)/(8х8біт) вагових коефіцієнтів - (2х32біти)/(2х32біти)
По приведених двох варіантах розбивки матриці векторного помножувача виробляється п
Таблиця 2. Порівняльна характеристика точності відновленого сигналу після прямого і зворотного ШПФ із різними основами
Перетворення Фур'є
Систематична похибка-M
СКО -s
6 біт/1.0
7 біт /1.0
6 біт/1.0
7 біт /1.0
Таблиця 3. Продуктивність функцій прямого і зворотного ШПФ на процесорі NM6403
Кільк. комплекс. відліків
Без нормалізації
З однією нормалізацією
З двома нормализациями
Тактів
Аналіз задач і алгоритмів
До основних галузей, де використовується опрацювання сигналів та зображень відносяться:
1. Радіолокація (РЛ) — виявлення, фільтрація сигналу з режекцією завад та накопичення сигналу.
Особливості задач і алгоритмів.
Аналіз наведених задач і алгоритмів їх розв’язання показує, що вони мають такі особливості:
- широкий динамічний і частотний діапазон сигналів, що обробляються;
- велика інтенсивн
Особливості організації обчислювальних засобів
1.2.1. Методи аналізу обчислювальних засобів архітектур.Технічно системи керування та опрацювання інформації реалізуються як комплекс спеціалізованих і універсальних засобів обчисл
Основні положення алгоритму ШПФ
Визначення 1. Дано кінцеву послідовність x0, x1, x2,..., xN-1 (у загальному випадку комплексних чисел). ДПФ полягає в пошуку послідовності
Основні формули
Теореми, що пояснюють суть перетворення Фур’є (наведені без доведення).
Теорема 1. Якщо комплексне число представлене у вигляді e j2πN, де N - ціле, то
Fft.cpp
/*
Fast Fourier Transformation
=====================================================
*/
#include "fft.h"
// This array contains values from 0
Організація DSP- процесорів для задач опрацювання сигналів та зображень
Для опрацювання сигналів та зображень найчастіше використовуються DSP- процесори. Розглянемо підходи до їх реалізації на базі обчислення алгоритму ШПФ.
В загальному випадку, вимоги по вико
Типова структура процесора опрацювання сигналів та зображень
На рис. 3.1 наведена спрощена система на базі процесора ADSP-2189M, що використовує повномасштабну модель пам'яті.
Нтерфейси DSP-процесорів
Ефективність роботи DSP- процесора в структурі системи залежить від організації каналів вводу-виводу. До складу сучасних DSP- процесорів (наприклад, ADSP-21ESP202) входять інтегровані АЦП/ЦАП, що з
Аналіз паралельного інтерфейсу з DSP-процесорами: читання даних з АЦП, що під’єднаний до адресного простору пам’яті
Підключення АЦП або ЦАП через паралельний інтерфейс до DSP-процесора вимагає розуміння специфіки процесів читання/запису даних DSP-процесором з/в периферійних пристроїв при їх під’єднані до
Аналіз паралельного інтерейсу з DSP-процесорами: запис даних в ЦАП, що під’єднаний до адресного простору пам’яті
Спрощена блок-схема інтерфейсу між DSP-процесором і наприклад ЦАП) наведена на рис. 4.4. Діаграми циклу запису в пам'ять для сімейства ADSP-21xx наведені на рис.6.
В системах реального час
Аналіз послідовного інтерфейсу з DSP-процесорами
Наявність послідовного порту усуває необхідність використання паралельних шин для підключення АЦП і ЦАП до DSP-процесорів.
Структурна схема одного з двох послідовних портів процесора сімей
Проектування процесора ШПФ на ПОС
Алгоритм ШПФ із проріджуванням за часом
Нехай
Розділимо послідовність x(n) на парні (ev
Аналіз (розробка) блок-схеми виконання алгоритму ШПФ на заданому типі процесора
Алгоритм базової операції ШПФ за основою 4 і проріджування за часом можна представити так:
А'1 = А1 + A2W1 + A3W2 + A
Розрахунок основних параметрів
Частота роботи процесора: , звідси цикл виконання команди:
Привабливою рисою ПЛІС для реалізації алгоритмів ЦОС є наявність внутрішнього швидкодіючого розподіленого ОЗП, вбудованих вузлів обчислення ШПФ тощо.
На рис. 6.1 наведена структурна схема вузла реалізації алгоритм ШПФ на ПЛІС. Вхідне ОЗП використовується для завантаження вхідної послідовності, збереження результатів проміжних обчислень і виванта
Оцінка продуктивності вузла реалізації алгоритму ШПФ на ПЛІС
Швидкодія виконання алгоритму ШПФ на ПЛІС визначається в NMAC (кількість операцій типу множення-нагромадження) за такою формулою:
Побудова граф-алгоритму ШПФ з основою 2 наведена в попередніх розділах.
При апаратній реалізації графу ШПФ виникають незручності через неспівпадіння адрес комірок пам'яті з яких потрібно вичитувати елементи на кожному ярусі. Тому на рис.6.2. наведений граф, де для кожн
Реалізація алгоритмів опрацювання сигналів та зображень на нейропроцесорах
Нейрокомпьютер - це обчислювальна система з MSІMD архітектурою, тобто з паралельними потоками однакових команд і множинним потоком даних. На сьогодні можна виділити три основних напрямки розвитку о
ВЕКТОРНИЙ СПІВПРОЦЕСОР
Векторний співпроцесор - основний функціональний елемент Л1879ВМ1. Структурно він являє собою матрично-векторний операційний пристрій і набір регістрів різного призначення.
Операційний при
Організація паралельних обчислень в алгоритмах ШПФ на процесорі NM6403
Значна частина задач аналізу часових рядів зв'язана з перетворенням Фур'є і методами його ефективного обчислення. У цих задачах перетворення Фур'є відіграє важливу роль як необхідний проміжний крок
Продуктивність і точність обчислень.
Точність обчислень визначається кількістю біт, що відводяться для представлення коефіцієнтівW. Є два способи представлення значень косинусів і синусів у 8 розрядній сітці:
1. W =round(64.0
Загальна характеристика функцій ШПФ.
Вхідні і вихідні дані - цілі 32р. комплексні числа, формат збереження наведений на рис.3
Діапазон вхідних даних зазначений у таблиці 3.
Розрядність коефіцієнтів перетворення - 8 б
Стиск нерухомих зображень з використанням дискретних косинусних перетворень
Безвтратні методи стиску не забезпечують потрібного у багатьох випадках степеня стиску зображень. У цьому разі необхідно застосовувати методи стиску з втратою інформації. Одним із найбільш поширени
Стиск нерухомих зображень з використанням хвилькових перетворень
Поняття хвилькового перетворення
Дискретне хвилькове перетворення (dyscrete wavelet transform (DWT)) принципово відрізняється від спектральних перетворень.
На рис.8.3 показано стр
Стиск зображень з використанням методу кодування областей хвилькового перетворення
У цьому методі розглядаються області коефіцієнтів логарифмічного хвилькового перетворення зображення, які мають різні розміри. Ідея полягає в тому, щоб коефіцієнти в різних областях опрацьовувати (
Стиск зображень з використанням методу дерев нулів хвилькового перетворення
Хвильковий розклад зображення можемо мислити собі як просторову множину коефіцієнтів, яка складається з дерев. Дерево коефіцієнтів хвилькового перетворення означається як множина коефіцієнтів із рі
Адаптивні хвилькові перетворення : Хвилькові пакети.
Слід зауважити, що традиційний підхід використання хвилькових перетворень з фіксованою частотною роздільною здатністю (логарифмічне хвилькове перетворення) є добрий лише в загальному для типового с
Опрацювання мовних сигналів
Багато напрямків мовних технологій (опрацювання мовних сигналів з певною метою: стиск мовних сигналів, cинтез мови, зміна темпу мовлення, розпізнавання або визначення емоційного стану людини за гол
Мовні технології
Виділяють такі напрямки мовних технологій.
1. Стиск (кодування) мови.
Високого степеня стиску досягаємо використанням дискретних косинусних перетворень.
2. Синтез мови
Алгоритм динамічного часового вирівнювання для розпізнавання слів з невеликого словника
На фазі навчання як мовні еталони записуємо якнайкоротше вимовлені диктором слова із заданого невеликого словника.
Сигнал, який розпізнаємо, та сигнали-еталони параметризуємо – перетворюєм
Розпізнавання злитної мови з великим словником
Сучасні системи для розпізнавання злитної мови з великим словником ґрунтуються на принципах статистичного розпізнавання образів.
На першому етапі мовний сигнал перетворюється звуковий преп
Просочування спектральних складових
Вибір кінцевого часового інтервалу тривалістю NT секунд і ортогонального тригонометричного базису на цьому інтервалі обумовлює цікаву особливість спектрального розкладу. 3 континууму можливи
Вікна та їх основні параметри
В гармонійному аналізі вікна використовуються для зменшення небажаних ефектів просочування спектральних складових. Вікна впливають на можливість виявлення, роздільну здатність, динамічний діапазон,
Класичні вікна
Всі наведені вікна представляються як парні (щодо початку координат) і містять непарну кількість точок. Для перетворення вікна в ДПФ-парне вікно достатньо відкинути крайню праву точку і зсунути пос
Гармонійний аналіз
Проаналізуємо вплив властивостей вікна на ефективність виявлення слабої спектральної лінії у присутності інтенсивної близько розташованої лінії. Якщо обидві спектральні лінії потрапляють в біни ДПФ
Висновки
В даному навчальному посібнику описані основні алгоритми опрацювання сигналів та зображень та шляхи їх реалізації. Основна увага приділена системному підходу, який дозволяє розв’язати певну задачу,
Література
1. Айфигер, Эммануил С., Джервис, Барри У. Цифровая обработка сигналов: практический поход, 2-е изд.: Пер. с англ. – М.: Издательский дом “Вильямс”, 2004. – 992с.
2. Цифров
Рархічність засобів обробки радіолокаційної інформації.
Обробка радіолокаційної інформації (РЛІ) як правило складається з декількох етапів.
Первинна обробка РЛІ здійснюється апаратурою радіолокаційної станції (АПОІ РЛС) з видачею інформа
Особливості обробки радіолокаційної інформації. Вибір параметрів радіолокаційної станції, які впливають на характеристики засобів обробки.
Параметри:
- вид сигналу;
- потужність сигналу;
- тривалість зондувального сигналу /Тс/;
- оброблюваний доплерівский діапазон частот /F/ ;
Вимоги до системи
1. Система повинна будуватися на сучасній елементній базі з використанням відповідних міжнародним стандартам конструктивов і інтерфейсів
2. Система повинна мати модульну структуру і будува
Елементна база
Орієнтація на два механічних конструктива і на дві стандартні системні шини приводить до того, що можуть існувати три різних типи уніфікованих модулів:
1. Система на основі ПЕОМ із шинами
Архітектура системи
Пропонується комбінована архітектура на основі поділюваної системної шини і конфігурованих користувачем високопродуктивних прямих з'єднань модулів між собою для рішення задач високопродуктивної обр
Апаратна реалізація мережі
Вузли обчислювальної мережі виконані на процесорах TMS320C40 (TMS320C44), до яких підключена зовнішня оперативна пам'ять ємністю 512-1024 кбайт. У залежності від реалізації процесорного модуля (TІМ
Найпростіша первинна обробка РЛИ на МП мережі
Для відпрацьовування і реалізації на мультипроцесорній мережі найпростішого алгоритму первинної обробки даних було розроблено функціональне програмне забезпечення (ФПЗ), що реалізує алгоритм, зобра
Обмежувач.
· Алгоритм обчи
Порогові пристрої.
У системі реалізовані порогові пристрої з ковзним порогом. Значення порога обчислювалося по формулі
Таблиця 1. Часові параметри модулів ФПЗ, отримані в симуляторі.
Програма
Цикли
Час, мкс
Кількість операцій ПК
Vmax, (MFLOP)
Vвузла, (MFLOP)
СРЦ
Таблиця 2. Експериментально виміряні часові параметри модулів ФПЗ.
Програма
Цикли
Час, мкс
Кількість операцій ПК
Vmax, (MFLOP)
Vвузла, (MFLOP)
СРЦ
Призначення ПФОС.
Пристрій формування й обробки сигналів /ПФОС/ входить до складу когерентної далеко-доплерівської радіолокаційної станції, що працює в імпульсному чи квазінеперервному режимі випромінювання і прийом
Принцип побудови і структура ПФОС.
Пристрій формування й обробки сигналів побудовано по модульному принципі з нарощуванням структури і складається з окремих взаємозамінних програмно-апаратних модулів. Кожен програмно-апаратний модул
Технічна реалізація модуля.
Модуль формування й обробки сигналів реалізований на основі пристроїв програмувальної логіки фірм Xіlіnx, Altera і сигнальних процесорів фірми Analog Devіces. Основні технічні характеристики модуля
Модуль кодуючого пристрою .
Кодуючий пристрій призначений для :
· забезпечення режимів роботи РЛС і необхідних робочих шкал дальності;
· формування модулюючих сигналів , що задають закон амплітудно-фазової м
Режими роботи ПФОС.
ПФОС забезпечує формування й обробку сигналів у двох режимах випромінювання і прийому складних амплітудно-фазоманіпуляційних сигналів:
· у квазінеперервному режимі випромінювання й обробки
Квазінеперервний режим випромінювання й обробки.
При квазінеперервному режимі фазоманіпуляційний сигнал з великою базою (В=<256K) випромінюється окремими імпульсами, тривалість і інтервал проходження яких визначається структурою дискретного си
Практичне використання результатів і перспективи розвитку.
В даний час пристрої формування й обробки сигналів (ПФОС) використовуються в розробках, виконаних разом з ведучими НПО і НДІ м. Санкт-Петербурга.
Розроблені РЛС успішно пройшли натурні вип


 Рис. 2.4
Рис. 2.4

 .
.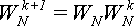 . (2.10)
. (2.10)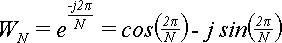

 не потрібно обчислювати двічі) замість 13. У найгіршому випадку для піднесення до ступеня від 1 до N/ 2-1 потрібно log2N множень замість N/2, що дає цілком прийнятну похибку для більшості практичних задач.
не потрібно обчислювати двічі) замість 13. У найгіршому випадку для піднесення до ступеня від 1 до N/ 2-1 потрібно log2N множень замість N/2, що дає цілком прийнятну похибку для більшості практичних задач. ,
,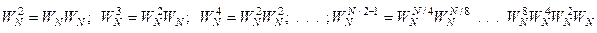
 не було обчислено попередньо, то береться двійкове представлення k і аналізується. Кожному одиничному біту відповідає рівно один множник. У загальному випадку одиниці в біті з номером b відповідає множник
не було обчислено попередньо, то береться двійкове представлення k і аналізується. Кожному одиничному біту відповідає рівно один множник. У загальному випадку одиниці в біті з номером b відповідає множник  , що зберігається в b-ій комірці масиву.
, що зберігається в b-ій комірці масиву. до одного на два цикли необхідно відвести N/2 комплексних комірок для зберігання всіх попередніх
до одного на два цикли необхідно відвести N/2 комплексних комірок для зберігання всіх попередніх  . Непарні елементи обчислюються за формулою (2.10). Парні обчислюються за формулою
. Непарні елементи обчислюються за формулою (2.10). Парні обчислюються за формулою 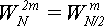 , тобто, нічого не обчислюється, а береться одне зі значень, обчислених на попередньому кроці, коли N було вдвічі менше. Щоб не потрібно було копіювати величини на нові позиції досить їх відразу розташовувати в тій позиції, що вони займуть при N = Nmax і вводити просте виправлення Skew.
, тобто, нічого не обчислюється, а береться одне зі значень, обчислених на попередньому кроці, коли N було вдвічі менше. Щоб не потрібно було копіювати величини на нові позиції досить їх відразу розташовувати в тій позиції, що вони займуть при N = Nmax і вводити просте виправлення Skew.






Новости и инфо для студентов