Математические модели и численные методы

1. Математическая постановка задачи и построение математической модели. На данном этапе требуется · определить, что дано, что надо получить; · выделить наиболее существенные свойства изучаемого объекта;

Структура погрешности при решении задачи на ЭВМ

R – точное решение задачи (результат); – приближенное решение задачи; ε – полная погрешность.

Решение уравнений с одной переменной

Постановка задачи

Рассмотрим уравнение вида F(x)=0, где F(x) – определенная и непрерывная на отрезке [a,b] функция.

Корнем уравнения F(x)=0 называется такое значение x^*, которое обращает уравнение в верное равенство.

x^* - корень уравнения F(x)=0 • x^* - нуль функции y=F(x).

Решить уравнение – значит установить, имеет ли оно корни, сколько корней, и найти их значения с заданной степенью точности.

Нахождение корней уравнения состоит из двух этапов:

I. Отделение корней – выделение промежутков, содержащих ровно 1 корень.

II. Уточнение корней – нахождение корней с заданной степенью точности.

Отделение корней

Отделение корней может осуществляться графически или программным путем.

I. Графический способ отделения корней

Если на отрезке [a,b] функция y=F(x) определена и непрерывна, и на его концах принимает значения разных знаков (т.е. F(a)F(b)<0), то уравнение…

II. Отделения корней программным способом.

Правильность нахождения отрезков, содержащих один корень, зависит от характера функции y=F(x) и от величины шага h.…

Уточнение корней

Уточнение корней может осуществляться различными методами.

Метод половинного деления

2) F(a)F(b)<0 Требуется найти корень на отрезке с точностью ε. Разделим отрезок [a,b] пополам точкой . Если , то возможны два случая: 1) F(x) меняет знак на отрезке [a; c];

Метод хорд

В качестве приближений к корню принимаются значения c0, c1, c2… точек пересечения хорды с осью абсцисс или Точка c делит отрезок [a,b] на две части. Ту из них, на которой функция знака… В качестве условия окончания счета можно принять условия:

Метод касательных

Требуется найти корень на отрезке с точностью ε. На kой итерации проводится касательная к графику функции y=F(x) при x=ck и… Уравнение касательной к графику функции y=F(x) в точке x0 имеет вид: . Пересечение с осью Ox находится из условия y=0,…

Метод простой итерации

Теорема. Пусть уравнение x=f(x) имеет единственный корень на отрезке [a,b] и выполнены… 1) функция f(x) определена и дифференцируема на отрезке [a,b];

Оценка погрешности метода итераций

Пусть x_n – приближение к истинному значению x^* корня уравнения x=f(x).

Абсолютная ошибка Dx_n=|x^*-x_n|.

Для оценки погрешности n-го приближения используется формула .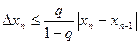

Значение q можно получить как верхнюю грань модуля производной |f’(x)| при xÎ[a,b]. Чем q меньше, тем быстрее сходится ряд.

Условие окончания счета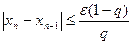

Преобразование к итерационному виду

Уравнение F(x)=0 приводится к равносильному уравнению x = x – m F(x), таким образом, f(x) = x – m F(x). Исходя из третьего условия теоремы: ($q) ("xÎ[a,b]) [… Достаточно подобрать m так, чтобы выполнялось неравенство 0<mF’(x)<1, откуда следует и .

Постановка задачи

Ее можно записать в матричном виде A x = B, где

Метод Гаусса

Рассмотрим систему m линейных уравнений с n неизвестными: Алгоритм состоит из двух этапов.

Метод простой итерации

1) r(x,y)³0 2) r(x,y)=0 • x=y 3) r(x,y)= r(y,x)

Решение СЛУ методом Зейделя

При решении СЛУ методом простой итерации каждый шаг итерационного процесса состоит в переходе от уже имеющегося приближения значений неизвестных к новому приближению.

Основная идея метода Зейделя состоит в том, что на каждом шаге итерационного процесса при вычислении значений y_i учитываются уже полученные значения y₁, y₂,…,y_i_-1.

Условие α<1 является достаточным для сходимости итерационного процесса метода Зейделя. Причем метод Зейделя обеспечивает более быструю сходимость, чем метод простой итерации.

Запишем формулы для решения системы методом Зейделя:

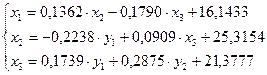
Интерполирование функций

Постановка задачи

Требуется получить y=f(x) для xÏ[x0,xn], где x¹xi. При этом аналитическое выражение · не пригодно ля вычислений либо · неизвестно.

Интерполяционный многочлен Лагранжа

. Погрешность вычисляется по формуле: , где

Интерполяционный многочлен Ньютона для равноотстоящих узлов

Рассмотрим конечные разности: – конечные разности 1-го порядка – разности между значениями функции в… – конечные разности 2-го порядка – разности между конечными разностями 1-го порядка.

Первая интерполяционная формула Ньютона

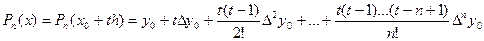– первая интерполяционная формула Ньютона.

Погрешность вычислений оценивается следующим образом:

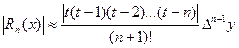
Так при n=2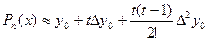

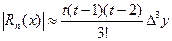, где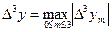

Вторая интерполяционная формула Ньютона

Вторая интерполяционная формула Ньютона применяется, когда значение аргумента ближе к концу отрезка интерполяции (формула для интерполирования назад). .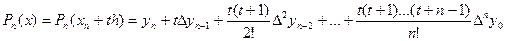

Погрешность вычислений оценивается следующим образом:

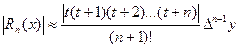Численное интегрирование

Для вычисления определенного интеграла используется формула Ньютона-Лейбница: ,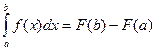

где F(x) – одна из первообразных функции f(x) (такая что F’(x)=f(x)).

Однако функция f(x) может быть задана таблицей или графиком, а также аналитически, но нахождение первообразной в аналитическом виде затруднительно. В этих случаях применяют методы приближенного (численного) интегрирования.

Формулы, используемые для приближенного вычисления однократных интегралов, называют квадратурными формулами.

Считая f(x) » L_n(x), на [a,b], получим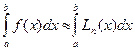

Формула трапеций

Формула 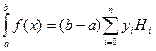на отрезке [x₀, x₁] имеет вид:

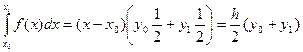
Для отрезка [a, b]: (*)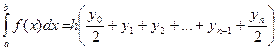

Погрешность: 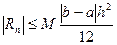, где .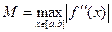

Программа численного интегрирования методом трапеций:

Блок-схема численного интегрирования методом трапеций:

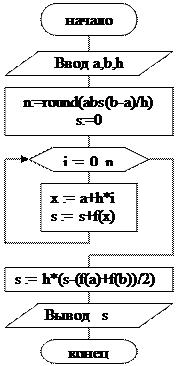
Формула Симпсона

Формула 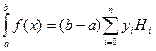на отрезке [x₀, x₂] имеет вид:

При n=2m применив формулу к каждой паре частичных отрезков [x_2i-2, x_2i] (i=1,2,…,m) получим формулу Симпсона:

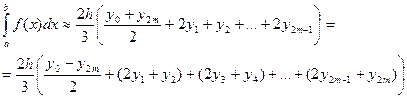
Погрешность: , где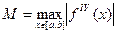

При вычислении по методу повторного счета можно использовать формулу: 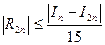. Если при вычислении интеграла требуемая точность не достигнута (т.е. 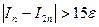), предусматривается повторный счет с шагом, уменьшенным вдвое.

Численное решение дифференциальных уравнений

Основные определения и постановка задачи

(1) Решением дифференциального уравнения (1) называется функция y(x), подстановка… График решения y=y(x) называется интегральной кривой.

Метод Эйлера

Угловой коэффициент касательной к интегральной кривой в точке M0(x0,y0) равен . Найдем ординату y1 касательной, соответствующей абсциссе x1=x0+h. Уравнение касательной к кривой в точке M0 имеет вид или , откуда y1=y0+hf(x0,y0).

Методы Рунге-Кутта

; (i=1, 2, …, m) (7) , Метод называют методом Рунге-Кутта порядка P, если от имеет P-й порядок точности по шагу h на сетке.

Классический метод Рунге-Кутта

Метод Рунге-Кутта четвертого порядка получаем при

P=4, c₁=0, c₂= c₃=1/2, c₄=1, d₁=d₄=1/6, d₂=d₃=1/3

Расчетные формулы имеют вид:

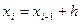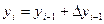; (i=1, 2, …, m) (9)

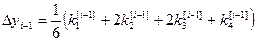
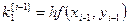
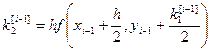
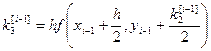
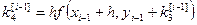
То есть берутся 4 направления и усредняются.

Для практической реализации погрешности решения можно применять правило Рунге, полагая P=4: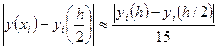

Метод наименьших квадратов

Постановка задачи

Поставим задачу об отыскании аналитической зависимости между x и y, т.е. некоторой формулы y=f(x). При этом потребуем, чтобы график искомой функции…

Нахождение приближающей функции в виде линейной функции

Рассмотрим приближающую функцию в виде F(x,a,b) = ax+b.

Наша задача – отыскать значения параметров a и b.

Существует показатель, характеризующий тесноту линейной связи между X и Y. Это (выборочный) коэффициент корреляции. Он вычисляется по формуле: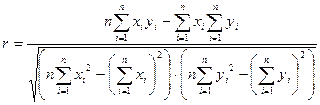

Значение коэффициента корреляции всегда удовлетворяет соотношению: -1£r£1. Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки.

Если коэффициент корреляции равен нулю, то говорят, что переменные X и Y некоррелированы.

Нахождение приближающей функции в виде других элементарных функций

1. Степенная функция: y=a x^m

Прологарифмируем: ln y = ln a + m ln x

Замена: m = A, ln a = B ln y = v ln x = u

Получим функцию v = A u + B

2. Показательная функция: y=a e^mx

Прологарифмируем: ln y = ln a + m x

Замена: m = A, ln a = B ln y = vx = u

Получим функцию v = A u + B

3. Логарифмическая функция: y=a ln x + b

Замена: a = A, b = B y = v ln x = u

Получим функцию v = A u + B