Лекция 5.Кинематика точки. Кинематика изучает движение с внешней стороны
Лекция 5.Кинематика точки
Кинематика изучает движение с внешней стороны, рассматривая лишь его геометрические свойства и временные характеристики - скорость и ускорение.
Объекты кинематики: точка и твердое тело, т.е. такое тело, расстояния между точками которого, не изменяются.
Основные задачи кинематики: 1) математическое описание движений точки и твердого тела; 2) определение кинематических характеристик движения точки (скорости, ускорения) и твердого тела (угловой скорости и углового ускорения).
Тело отсчета – тело, относительно которого рассматривается движение других тел. Система отсчета - это тело отсчета, с которым связана система координат для измерения расстояний и часы - для измерения времени.
Способы описания движения точки
Все современные математические способы описания движения используют две основные идеи, автором которых, по-видимому, является Р.Декарт (1637): 1)… Координатный способ. Пусть задана система координат, жестко связанная с телом… , , . (5.1)Вектор скорости
Скорость характеризует быстроту и направление движения точки, поэтому естественно определить её как вектор перемещения точки Dr= = r(t+Dt) - r(t),… (5.4) Недостатком такого определения будет зависимость скорости от продолжительности Dt промежутка времени [t, t + Dt] на…Ускорение точки
Ускорение точки характеризует быстроту изменения её скорости и играет исключительно важную роль в динамике. Это видно из того, что ускорение входит… Пусть Dv= v(t + Dt) - v(t) - изменение вектора скорости за промежуток времени… (5.7)Вычисление скорости и ускорения точки
При координатном описании её движения.
Пусть движение точки М в декартовой системе координат (рис.1) задано уравнениями вида (5.1). Разложение радиус-вектора r точки М по базисным векторам i, j, k имеет вид: … r = xi + yj + zk (5.8)Вычисление скорости и ускорения точки
При естественном описании движения.
Пусть задана траектория движения точки М, а на ней указано начало О и положительное направление отсчета дуговой координаты s. Пусть также задано… Рассмотрим радиус-вектор r точки М относительно какого-нибудь неподвижного… Итак, вектор скорости точки:Задания для самостоятельной работы
1. Чем отличаются величины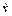 и
и 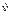 ?
?
2. Какой характер имеет движение точки при выполнении следующих условий :
а)  ;
;
б) 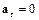 ;
;
в)  ,
, 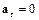 .
.
3. Какое направление имеет вектор ускорения точки при её равномерном движении по окружности?
Приложение 1. Сведения из дифференциальной геометрии
Касательной к кривой К в точке М называют предельное положение секущей, проходящей через М и соседнюю точку М1 этой же кривой при стремлении М1 к точке М. Радиус-вектор точки кривой является функцией дуговой координаты r = r(s), поэтому орт t0 касательной выражается в виде :

 Откуда следует, что положительное направление касательной Мt совпадает с направлением отсчета дуговой координаты s.
Откуда следует, что положительное направление касательной Мt совпадает с направлением отсчета дуговой координаты s.
Соприкасающейся окружностью кривой К в точке М называют предельное положение окружности, проходящей через М и две соседние точки этой же кривой М1 и М2 при стремлении М1 и М2 к М . Центр соприкасающейся окружности называют центром кривизны, а ее радиус r - радиусом кривизны кривой К в точке М.
 Кривизной кривой К в точке М называют величину k обратную радиусу кривизны. Другое определение кривизны - предел отношения угла поворота Dq касательной к соответствующему изменению Ds дуговой координаты
Кривизной кривой К в точке М называют величину k обратную радиусу кривизны. Другое определение кривизны - предел отношения угла поворота Dq касательной к соответствующему изменению Ds дуговой координаты
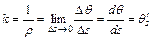
Ось Мn , идущая из точки М в центр кривизны называется главной нормалью кривой К в точке М.
Плоскость соприкасающейся окружности называют соприкасающейся плоскостью кривой К в точке М. Можно определить соприкасающуюся плоскость и как предельное положение плоскости, которая проходит через касательную Мt и параллельна касательной М1t , при стремлении точки М1 к точке М .
Из этих определений ясно, что касательная Мt и главная нормаль Мn лежат в соприкасающейся плоскости и взаимно перпендикулярны.
Направление орта t0 касательной Мt зависит от дуговой координаты s точки М , следовательно t0 = t0(s). Вычислим производную

Здесь n0 - орт главной нормали кривой .
 Бинормалью к кривой К в точке М называют ось Мb, проходящую через точку М и образующую с касательной Мt и главной нормалью Мn правую тройку взаимно перпендикулярных осей (рис.10).
Бинормалью к кривой К в точке М называют ось Мb, проходящую через точку М и образующую с касательной Мt и главной нормалью Мn правую тройку взаимно перпендикулярных осей (рис.10).
Касательную Мt , главную нормаль Мn и бинормаль Мb называют естественными осями кривой К в точке М.