Суть современного аксиоматического метода заключается в следующем.

Во-первых, понятия об основных объектах математической теории, отношениях и связях между ними называются и полностью перечисляются, но однозначно не определяются, рассматриваются как переменные, кото­рым можно придавать различный конкретный смысл.

В геометрии, например, основными понятиями являются «точка», «прямая», «плоскость», а отношения между ними, выражены словами: «точка ле­жит на прямой» или «точка лежит между двумя другими точками» т.п.

Во-вторых, основные положения теории задаются как описания структуры, т.е. составляется список конечного числа аксиом, которым должны подчиняться указанные выше основные понятия (в остальном природа основных понятий безразлична).

Система аксиом должна удовлет­ворять следующим требованиям.

1. Требованию непротиворечивости, или со­вместности: ни одна из аксиом не должна про­тиворечить другим аксиомам этой системы, сле­довательно, и следствия из них не должны при­водить к противоречиям.

При содержательном аксиоматическом обосновании теории, когда основные ее понятия и аксиомы являлись отражениями свойств определенных реальных объектов, например определенных прост­ранственных форм, как у Евклида, вопрос об истинности системы аксиом возникнуть не мог. Напротив, когда система основных поня­тий, отношений и аксиом задана формально, задача аксиомати­ческого обоснования теории вступает во вторую фазу своего раз­вития: надо показать хотя бы одну область объектов, структура отношений между которыми описывается заданной системой ак­сиом.

Действительно, если такая область объектов существует, то определяемая системой тео­рия правильна, как правильна всякая тео­рия, дающая верное отражение той или иной стороны природы. Правильную систему аксиом спра­ведливо называют совместной или непротиворечивой. Более общим об­разом непротиворечивость означает выполнимость или возможность построения области объектов, так как система аксиом может опи­сывать не только существующие объекты, но и такие, которые можно построить.

Напротив, противоречивость (несовместность) системы аксиом свидетельствует о ее ложности. Каждая противоречивая система аксиом не отражает соотношений ни в одной области вещей и как бессодер­жательная исключается из математики.

Для доказательства выполнимости (непротиворечивости) при­бегают обычно к методу моделей. Из объектов некоторой теории В, непротиворечивость которой считается установленной, стараются создать интерпретацию, как говорят, модель рассматриваемой систе­мы аксиом А. Создание модели гарантирует непротиворечивость системы А. Действительно, в этом случае все аксиомы системы А становятся предложениями теории В, и если бы из А следовало противоречие, то теория В была бы противоречивой. Например, для доказательства непротиворечивости геометрии Евклида непротиворечивой теорией считают учение о действительных числах. Из действительных чисел создают «точки», «прямые» и «плоскости» (подобно тому, как это делают в аналитической геометрии). Гово­рят, далее, что надо понимать под основными отношениями, в которых могут выступать «точки», «прямые» и «плоскости», и показывают, что при этих условиях структура отношений «то­чек», «прямых» и «плоскостей» описывается системой аксиом Евклида. Подобным же путем непротиворечивость учения о действитель­ных числах можно соподчинить вопросу о непротиворечивости уче­ния о рациональных числах.

Метод моделей не дает автономного доказательства непротиво­речивости теории, но только сводит вопрос о непротиворечи­вости одной теории к вопросу о непротиворечивости другой теории. Путем таких сведений удается показать, что вопрос о непротиво­речивости большинства математических теорий приводится к во­просу о непротиворечивости арифметики натуральных чисел (сле­довательно, требование доказательства непротиворечивости ариф­метики не является лишним). Таким образом, по крайней мере для одной математической теории доказательство ее непротиворечи­вости должно быть получено вне математики, т.е., очевидно, в практике.

Если для системы аксиом А построить модель не удается, то отсюда не следует ее противоречивость. Противоречивость должна быть доказана путем непосредственного получения противоречия из аксиом А или путем доказательства неосуществимости модели.

Иногда получить противоречие нетрудно. Возьмем, например все аксиомы геометрии Евклида, за исключением аксиомы о парал­лельных. Эти аксиомы входят как в геометрию Евклида, так и в геометрию Лобачевского. В их числе находится аксиома Архимеда, которая (в терминах арифметики) утверждает: каковы бы ни были действительные числа х и у, 0 < х < у, существует такое натураль­ное число п, для которого пх > у. Из такой системы аксиом можно развить геометрию, которую Я. Больяй назвал абсолютной. Абсо­лютная геометрия непротиворечива и содержит факты, являющиеся общими для геометрии Евклида и Лобачевского. Частично эти факты изложены Евклидом в 27 первых предложениях первой кни­ги его «Начал».

Образуем теперь новую систему аксиом, для чего присоединим к аксиомам абсолютной геометрии утверждение: сумма углов тре­угольника больше 2d. Покажем, что так полученная система ак­сиом противоречива. Построим треугольники (см. черт. 1).

.

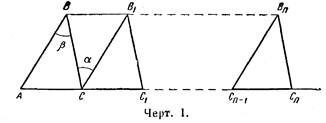
По нашему предположению сумма углов треугольника больше 2d, то β>α и, следовательно, АС>ВВ₁. Положим С_iС_i+1=В_iВ_i+1 + ε, где, ε =const. Так как отрезок прямой есть кратчайшее расстояние между двумя точками, то

АВ + BB₁ + . . . + В_п-1В_п + В_nС_n > АС + СС₁ + ... + C_п-1C_п,

откуда

АВ + ВС + пВВ₁ >(п + 1) (BB₁ + ε)

и после упрощения, const > nε при всяком натуральном п. Мы пришли к противоположному аксиоме Архимеда утверждению. Отсюда следует, что в каждой области объектов, удовлетворя­ющей аксиомам абсолютной геометрии, сумма углов треугольника не может быть больше 2d, или, иначе, что принятая нами система непротиворечива.

В реальности попытки установить противоречивость некоторых систем аксиом связаны с огромными трудностями. Например, никто до сих пор не смог доказать, что система аксиом арифметики, пополненная утверждением, обратным великой теореме Ферма, противоречива.

2. Требованию независимости: ни одна из аксиом рассматриваемой системы не может быть следствием других. Установить незави­симость аксиомы а_i от остальных аксиом непротиворечивой системы А - значит доказать непротиворечивость другой системы аксиом, отличающейся от А только одной аксиомой, противоположной а_i.

Доказательство независимости аксиомы параллельных от остальных аксиом геометрии Евклида было исторически первым примером доказательств такого рода, которое привело к открытию неевклидовой геометрии. Как видим, доказать независимость аксиомы - значит обосновать новую теорию.

3. Требование полноты непротиворечивой систе­мы аксиом геометрии заключа­ется в том, что она позволяет, не опираясь на наши наглядные представления и опыт, без до­бавочных соглашений, исключительно логиче­ским путем решить вопрос о доказуемости или недоказуемости любого геометрического предло­жения (теоремы), т.е. на основе полной системы аксиом из всяких двух взаимно противоречащих геометрических предложений одно всегда может быть доказано, а другое - опро­вергнуто.

Говорят также, система аксиом А называется полной, если любое свойство, принадлежащее объектам каждой ее интерпретации, может быть доказано с помощью системы А.

В указанном смысле полнота в большинстве случаев почти не­достижима, или, лучше сказать, достижима асимптотически; не­сомненно, что система аксиом Евклида, данная Гильбертом, более полна, чем система аксиом Евклида. Учитывая это обстоятельство, а также и то, что внимание современной математики направлено в частности на изучение структуры качественно различных, но изоморфных областей объектов, довольствуются таким определе­нием полноты: система аксиом полна, если все ее интерпретации необходимым образом изоморфны. В этом смысле, например, данная Гильбертом система аксиом геометрии Евклида полна.

В-третьих, каждая теорема теории должна быть доказана с помощью только ее основных утверждений и средств логики.