Исследования Саккери, Ламберта, Лежандра.

Постулаты параллельности Евклида и Лобачевского и их связь с вопросом о сумме углов треугольника и вопросом о существовании подобных фигур.

В XVIII в. созрели необходимые предпо­сылки для возникновения новых идей, связанных с геометрией Лобачевского, отрицающей V пос­тулат и все его эквиваленты. Нашлись ученые, которые были близки к этим идеям. Но, скован­ные старыми традициями, воспитанные на «На­чалах» Евклида и уверенные, что V постулат рано или поздно все же будет доказан (на ос­новании аксиом абсолютной геометрии), они слегка приоткрывали дверь в новую геометрию, даже заглядывали в этот новый мир, но тут же, пораженные его необычностью и несоответстви­ем своим наглядным представлениям, шараха­лись в сторону от этой двери, и она наглухо за­крывалась перед ними.

К этим ученым принадлежали итальянский математик Саккери (1667 - 1733), швейцарский ученый Ламберт (1728 - 1777), французский математик Лежандр. Они являются сти­хийными предшественники открытия Лобачевско­го. Ими были получены первые теоремы неевклидовой геометрии. В то время в геометрических представлениях старое было куда сильнее нового. Поэтому эти ученые вели исследования не для утвер­ждения новых идей, а чтобы похоронить эти идеи и доказать вместе с V постулатом незыблемость «Начал» Евклида, как единственно возможной геометрии.

Исследования Саккери. Саккери принадлежавший к ордену иезуитов, все свободное время отдавал изучению «Начал» Евклида и их критическому разбору. Результаты своих исследований он оформляет в виде трактата под ха­рактерным названием «Евклид, очищенный от всех пятен, или опыт, устанавливающий самые первые принципы универсальной геометрии» (1733 г.).

Для доказательства V постулата Саккери строил четырехугольник ABCD, у которого углы А и В при нижнем основании прямые, а боковые стороны AD и ВС рав­ны (рис. 6). Такие че­тырехугольники приня­то называть четырех­угольниками Саккери. Специальной теоремой Саккери доказывает, что углы С и D при верхнем основании рав­ны. Поэтому имеем, полное право каждый из этих углов обозна­чать через α. Относительно величины угла α Саккери устанавливает три гипотезы:

1) гипотезу тупого угла, согласно которой угол α тупой;

2) гипотезу прямого угла, согласно которой угол α прямой;

3) гипотезу острого угла, согласно которой угол α острый.

Саккери доказывает, что гипотеза прямого угла эквивалентна V постулату. Для доказа­тельства V постулата он старается, не прибегая к его эквивалентам, логически установить, что угол α прямой, т.е. из трех гипотез имеет мес­то только одна, а именно - вторая.

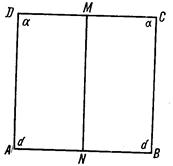
Рис. 6

 

Саккери устанавливает, что гипотеза тупого угла приводит к противоречию и, значит, должна быть отвергнута. Приняв гипотезу острого угла, Сакке­ри получает ряд следствий, противоречащих привычным гео­метрическим представлениям. Однако понимая, что нельзя отвергнуть гипотезу острого угла только на том основа­нии, что основанные на ней выводы приводят к утверждениям, противоречащим наглядным представлениям, Саккери ищет логиче­ское противоречие. Такое логическое противоречие, как ему кажется, он находит, однако оно оказывается следствием вы­числительной ошибки.

Он пишет: «При гипотезе тупого уг­ла дело ясно, как свет божий... Между тем оп­ровергнуть гипотезу острого угла мне не удается иначе, как доказав, что длина эквидистанты равна длине ее прямолинейного базиса...» Опре­деляя длину кривой методом бесконечно малых, Саккери допустил ошибку, приведшую его к не­верному заключению о том, что длина дуги экви­дистанты равняется ее проекции на ось, или, как он выражается, «длина эквидистанты равна дли­не ее прямолинейного базиса».

Свойства четырехугольника Саккери, относящиеся к абсолютной геометрии.

Свойство 1. Четырехугольник Саккери имеет ось симметрии, проходящую через середины оснований; эта ось является общим перпендикуляром к основаниям. Углы при верхнем основании четырехугольника Саккери равны и не превосходят .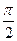

Свойство 2. Пусть в четырехугольнике углы при нижнем основании прямые, а боковые стороны не равны. Тогда из двух углов при верхнем основании больше тот, который лежит против большей стороны. Справедливо и обратное утверждение.

Убежденный в безупречности евклидо­вой геометрии, Саккери, сам того не сознавая, получил следующие результаты неевклидовой геометрии на плоскости:

1. Если в одном четырехугольнике Саккери угол α острый, то и во всяком четырехугольнике Саккери этот угол острый.

2. Сумма внутренних углов любого четырех­угольника меньше 4d.

3. Сумма внутренних углов любого треуголь­ника меньше 2d.

4. Перпендикуляр и наклонная к одной и той же прямой могут и не пересекаться.

5. Два перпендикуляра к одной и той же прямой, расположенные в одной плоскости, без­гранично расходятся один относительно другого.

6. Существуют прямые, которые, взятые по две, в одну сторону безгранично расходятся, а в другую - асимптотически сближаются (как увидим далее, такие прямые Лобачевский назвал параллельными).

7. Геометрическое место точек, равноудален­ных от данной прямой и расположенных по одну сторону от нее, на плоскости есть кривая (эквидистанта), имеющая с прямой не более двух общих точек.

В шестом и седьмом предложении Саккери и усмотрел противоречие. О «противоречии» в седьмом предложении было сказано выше. Что касается шестого предложения, то рассуждения Саккери сводились к следующему. Раз существу­ют две прямые, безгранично расходящиеся друг от друга в одну сторону и асимптотически сбли­жающиеся в другую, то на стороне их асимптоти­ческого сближения, по его мнению, в бесконечно­сти найдется точка, общая этим прямым, и в этой точке рассматриваемые прямые будут иметь об­щий перпендикуляр, что, как полагает Саккери, «противно нашему разуму».

Исследования Ламберта. Намного дальше Саккери и более смело по­шел по «дороге открытий» швейцарский ученый-самоучка, сын бедного ремесленника, достигший при жизни большой славы исследователя в обла­сти математики, астрономии, геодезии и фотомет­рии, член Берлинской академии наук Ламберт. Его можно считать непосредственным продолжа­телем идей Саккери.

Свои исследования Ламберт изложил в рабо­те «Теория параллельных линий», написанной, как полагают, в 1766 г. и опубликованной стара­ниями Бернулли и Гинденбурга в 1786 г.

Работу Ламберта можно разделить на три ча­сти. В первой части автор пытается решить воп­рос, можно ли V постулат получить как простое следствие из предшествующих постулатов или же для этого потребуются другие, более очевид­ные дополнительные постулаты. Во второй части даются различные попытки доказательства V по­стулата при помощи дополнительных постулатов, которые, являясь эквивалентами, сами должны быть доказаны. В третьей, наиболее интересной части излагаются, по существу, элементы неев­клидовой геометрии в том случае, когда наряду с аксиомами абсолютной геометрии имеет место «третья гипотеза». На этой третьей части работы Ламберта и остановимся несколько подробнее.

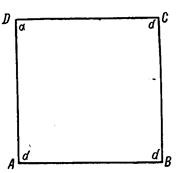
Рис. 7

 

В своих рассуждениях Ламберт исходит из четырехугольника ABCD, у которого три угла А, В и С заведомо прямые. Этот четырехугольник принято называть четырехугольником Ламберта. Строится он так. Из концов произвольного отрез­ка АВ восставляем перпендикуляры. На одном из них берем точку D (рис. 7) и из нее опускаем на другой перпендикуляр DC. Полученный четырех­угольник и будет иско­мым. Углы А, В, С будут прямые по построению. Величину угла D обозна­чим через α.

Относительно четвертого угла высказываются три гипотезы: этот угол прямой, тупой или острый. Ламберт устанавливает, что гипотеза прямого угла эквивалентна V по­стулату, гипотеза тупого угла противоречит остальным аксио­мам геометрии. Приняв гипотезу острого угла, он развивает на ее основании целую систему далеко идущих следствий, многие из которых противоречат наглядным представлениям о свой­ствах прямых. Однако Ламберт, как Саккери, ищет логическое противоречие. В отличие от Саккери он не сделал ошибки, в результате которой можно было бы отвергнуть гипотезу острого угла. Напротив, в своем сочинении Ламберт пишет: «Доказа­тельство евклидова постулата может быть доведено столь дале­ко, что остается, по-видимому, ничтожная мелочь. Но при тщательном анализе оказывается, что в этой кажущейся мело­чи и заключается вся суть вопроса; обыкновенно она содержит либо доказываемое предложение, либо равносильный ему по­стулат». Среди геометров XVIII в. Ламберт ближе всех стоял к верному решению проблемы V постулата.

Он даже вы­сказывает для того времени «еретическую» мысль. «Я почти принужден заключить, - пишет Лам­берт, - что третья гипотеза (острого угла) находит себе применение на некоторой мнимой сфере». Эти слова оказались пророческими. Действительно, много позднее Лобачевский показал, что все фор­мулы неевклидовой геометрии получаются из фор­мул сферической тригонометрии, если радиус R основной сферы, на которой строится тригономет­рия, заменить мнимым радиусом Ri, где i² = -1.

Ламберт сформулировал (но не доказал) тео­рему, что при наличии гипотезы острого угла площадь треугольника ABC пропорциональна его угловому дефекту, причем, под последним он по­нимал разность между двумя прямыми углами и суммой внутренних углов треугольника, т.е. S = ρ²δ, где S – площадь прямоугольного треугольника, ρ² – положительный множитель пропорциональности; δ – угловой дефект

δ = 2d – A – B – C.

Так как дефект треугольника не может быть отрицательным, то из полученной формулы Лам­берта как следствие вытекает, что площадь тре­угольника не может возрастать беспредельно. Как бы ни увеличивали мы стороны треугольни­ка, раздвигая его вершины, площадь треугольни­ка всегда будет оставаться меньше некоторой постоянной величины (константы). В геометрии Евклида если увеличить стороны треугольника, то площадь его возрастает беспредельно.

Здесь налицо полная аналогия со сферической геометрией (и тригонометрией), где роль прямых играют дуги больших кругов основной сферы, т.е. тех кругов, центры которых находятся в центре сферы. Как известно, формула площади сфериче­ского треугольника ABC имеет вид S = ρ²(-δ)

Если в этой формул радиус сферы ρ заменить через ρi, то получим формулу Ламберта, спра­ведливую при господстве гипотезы острого угла.

Нас, конечно, не удивляет, что в сферической геометрии площадь сферического треугольника всегда ограничена сверху и не может возрастать беспредельно, она, например, не может стать больше поверхности всего шара, так пусть же нас не удивляет и тот факт, к которому пришел Ламберт, что при наличии гипотезы острого угла площадь треугольника не может возрастать бес­предельно и всегда остается меньше некоторой величины.

В своих рассуждениях Ламберт зашел на­столько «далеко», что, приняв гипотезу острого угла, пришел к выводу, что должна существовать некоторая длина, характерная для нашего прост­ранства (абсолютная единица длины). Этот ре­зультат 60 лет спустя был заново открыт Н. И. Лобачевским.

Исследования Лежандра.Так же как Саккери и Ламберт, Адриен Мари Лежандр (1752-1833, Франция) пытается доказать утверждение V постулата методом от противного. За основу своих рассуждений Лежандр выбирает эквивалентное V посту­лату утверждение о том, что сумма углов треугольника равна 180°, и рассматривает три гипотезы: сумма углов треугольника больше 180°, равна 180° и меньше 180°. Первая гипотеза отвергается, поскольку противоречит остальным аксиомам гео­метрии. Вторая гипотеза эквивалентна V постулату. Отверг­нуть третью гипотезу Лежандру не удалось.