рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Используемые при изложении курса физики.
Реферат Курсовая Конспект
Используемые при изложении курса физики.
Используемые при изложении курса физики. - раздел Образование, Гироскопы 1. Графический Смысл Производной От Функции Y(X) По А...
1. Графический смысл производной от функции y(x) по аргументу x и интеграла от y(x) в пределах значений аргумента от x1 до x2.
Для определения производной функции y по аргументу x при каком-либо значении x = х0 необходимо взять конечные приращения аргумента x
(Δx = x1 - x2) и функции у (Δу = у1 - у2) и затем устремить Δx к нулю, т.е. взять бесконечно малые приращения dх и dу (их также называют элементарными приращениями). Тогда производная у ' будет равна
 (1)
(1)
и графически у ' представляет собой тангенс угла наклона касательной к графику функции в данной точке (рис.1а)
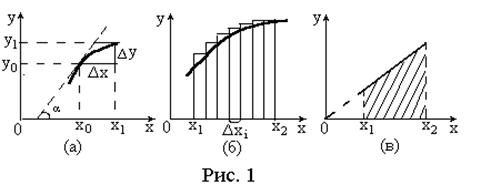
Графически интеграл от функции у в пределах значений аргумента от х1 до х2 представляет собой площадь под графиком функции в пределах от х1 до х2 (рис. 1.б.). Для ее расчета разбивают интервал (х1, х2) на малые участки Δxi(i=1,…,N), определяют площади прямоугольных полосок (уiΔхi) и затем их суммируют..
Точное значение площади под графиком функции получают при стремлении N→ ∞, Δxi→ dx и бесконечная сумма бесконечно малых величин (ydx) обозначается в виде интеграла
 (2)
(2)
Так, в частности, для прямолинейной зависимости у = bx интеграл будет равен площади трапеции (рис. 1.в.) и поэтому

Приведем необходимые для дальнейшего изложения материала ряд формул табличных интегралов
 , (3)
, (3)
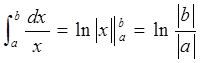 , (4)
, (4)
 , (5)
, (5)
 , (6)
, (6)
2. Скалярное произведение двух векторов  и
и  . Это скалярная величина, равная произведению модулей векторов
. Это скалярная величина, равная произведению модулей векторов  и
и  , умноженного на косинус угла α между ними
, умноженного на косинус угла α между ними
(
 ) = (
) = (
 ) = abcosα = baa ,
) = abcosα = baa ,
где в формулу введена проекция вектора  на направление вектора
на направление вектора 
(ba = bcosα, рис. 2а.).

Скалярное произведение произвольного вектора  на его вектор элементарного приращения d
на его вектор элементарного приращения d можно записать в следующем виде (рис. 2б.)
можно записать в следующем виде (рис. 2б.)
 d
d =
= ,
,
где dc – элементарное приращение модуля вектора  , оно может принимать как положительные, отрицательные, так и нулевые значения. В частности, это относится к элементарным приращениям модулей радиус-вектора
, оно может принимать как положительные, отрицательные, так и нулевые значения. В частности, это относится к элементарным приращениям модулей радиус-вектора  (dr), линейной скорости
(dr), линейной скорости (dv), угловой скорости
(dv), угловой скорости  (dω), и т.д. Для вектора же элементарного углового перемещения
(dω), и т.д. Для вектора же элементарного углового перемещения 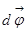 по определению dφ всегда больше нуля.
по определению dφ всегда больше нуля.
3. Векторное произведение векторов  и
и  . Это вектор
. Это вектор , равный по модулю произведению модулей векторов
, равный по модулю произведению модулей векторов  и
и  на синус угла α между ними (рис. 2в.).
на синус угла α между ними (рис. 2в.).
 =[
=[ ´
´ ] , с = ав cosα , α = (
] , с = ав cosα , α = ( ,
, )
)
Вектор  перпендикулярен плоскости вектора
перпендикулярен плоскости вектора  и
и , его направление можно найти по трем эквивалентным правилам: 1) правило правого буравчика. – вращательное движение буравчика должно совпадать с направлением кратчайшего поворота от
, его направление можно найти по трем эквивалентным правилам: 1) правило правого буравчика. – вращательное движение буравчика должно совпадать с направлением кратчайшего поворота от  к
к  , тогда его поступательное движение дает направление
, тогда его поступательное движение дает направление  ; 2) правило левой руки: – четыре пальца нужно расположить по направлению вектора
; 2) правило левой руки: – четыре пальца нужно расположить по направлению вектора  , вектор
, вектор  должен входить в ладонь, тогда отогнутый на 900 большой палец покажет направление
должен входить в ладонь, тогда отогнутый на 900 большой палец покажет направление  ; 3) правило векторного произведения: если смотреть с конца вектора
; 3) правило векторного произведения: если смотреть с конца вектора  на плоскость векторов
на плоскость векторов  и
и  , то тогда кратчайший поворот от
, то тогда кратчайший поворот от  к
к  будет направлен против часовой стрелки.
будет направлен против часовой стрелки.
4. Двойное векторное произведение векторов  ,
, и
и  раскрывается следующим образом
раскрывается следующим образом
[ [
[ ´
´ ]=
]= (
(
 )-
)- (
(
 ) (7)
) (7)
5. Градиент скалярной величины  . Пусть в пространстве каким-либо образом распределена скалярная величина
. Пусть в пространстве каким-либо образом распределена скалярная величина  (существует поле скалярной величины а) – это может быть поле температуры (
(существует поле скалярной величины а) – это может быть поле температуры ( = T), плотности вещества (
= T), плотности вещества ( = ρ), потенциальной энергии (
= ρ), потенциальной энергии ( = Wр) и т.д. Такое поле можно охарактеризовать максимальным и минимальным значением
= Wр) и т.д. Такое поле можно охарактеризовать максимальным и минимальным значением  , средним значением
, средним значением  , а также градиентом
, а также градиентом  . Под градиентом скалярной величины понимают вектор, который в каждой точке пространства направлен в сторону наиболее быстрого возрастания
. Под градиентом скалярной величины понимают вектор, который в каждой точке пространства направлен в сторону наиболее быстрого возрастания  и численно равный приращению величины
и численно равный приращению величины  на единицу длины этого направления
на единицу длины этого направления
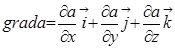 ,
, 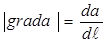 , (8)
, (8)
где  - направление grad
- направление grad в данной точке пространства; вектора
в данной точке пространства; вектора 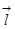 ,
, 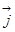 ,
, 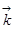 - вектора единичной длины (|
- вектора единичной длины (| |=|
|=| |=|
|=| |), указывающие направления осей Oх, Oу, и Oz в пространстве (рис. 3.). Они позволяют представить произвольный вектор
|), указывающие направления осей Oх, Oу, и Oz в пространстве (рис. 3.). Они позволяют представить произвольный вектор
 в виде суммы его проекции на оси (рис.3)
в виде суммы его проекции на оси (рис.3)
 =
=
 +
+
 +
+
 (9)
(9)
При вычислении производной величины  по координате x в формуле (8) считается, что координаты y и z остаются постоянными – такая производная называется частной производной по координате x
по координате x в формуле (8) считается, что координаты y и z остаются постоянными – такая производная называется частной производной по координате x


Аналогичные предположения принимаются при расчете частных производных по координатам y и z.
Выражение (8) можно записать в более компактном виде, если ввести оператор Гамильтона или оператор Набла
 (10)
(10)
Действие этого оператора на скалярную величину  приводит к выражению (8), т.е. grad
приводит к выражению (8), т.е. grad =
=
 .
.
– Конец работы –
Эта тема принадлежит разделу:
Гироскопы
Под гироскопом понимают быстро вращающееся симметричное твердое тело ось вращения которого ось симметрии может произвольно изменять свое...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Используемые при изложении курса физики.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов