Теорема Жегалкина

Каждая функция из может быть представлена в виде полинома Жегалкина единственным образом.

Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:

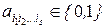, s = 0, 1, ..., n. Доказательство. Любая функция из Р₂ может быть представлена формулой над {x₁ & x₂, x₁Å x₂, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции f(x₁, ..., x_n) от n переменных. Мы знаем, что всего таких функций, т.е. их таблиц истинности , 2ⁿ. Подсчитаем число различных полиномов Жегалкина от n переменных, т.е. число вариаций вида: . Число наборов равно числу всех подмножеств множества { x₁, ..., x_n }, сюда входит и пустое множество (если s = 0). Число подмножеств множества из n элементов равно 2ⁿ , а так как каждый набор входит с коэффициентом , принимающим два значения: 0 или 1, то число всевозможных полиномов будет . Так как каждому полиному соответствует единственная функция, число функций от n переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.

Определение.Функция f(x₁, ..., x_n), полином Жегалкина для которой имеет следующий линейный относительно переменных вид: f = а₀ Å а₁х₁ Å а₂х₂ Å ... Å а_nх_n, называется линейной.

Лемма о нелинейной функции. Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.

Доказательство. Пусть f(x₁, ..., x_n) – нелинейная функция. Тогда полином Жегалкина содержит для нее слагаемое, в котором присутствует произведение x_ix_j. Будем считать для простоты, что x₁x₂ в многочлене Жегалкина является этим произведением. Произведя группировку слагаемых, функцию f представим в виде

Функция h₀ не есть тождественный нуль, иначе в полиноме Жегалкина отсутствует слагаемое с произведением x₁x₂. Тогда существует набор (a₃, …, a_n) из 0 и 1, для которого h₀(a₃, …, a_n) = 1. Пусть h₁(a₃, …, a_n) = a, h₂(a₃, …, a_n) = b, h₃(a₃, …, a_n) = c. Тогда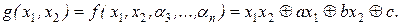

Построим функцию:

где d = ab Å c. Если d = 0, то h(x₁, x₂) = x₁x₂. Если d = 1, то h(x₁, x₂) = x₁x₂ Å 1 и тогда Лемма доказана.

Функция f(x₁, ..., x_n) сохраняет константу a Î {0, 1}, если f(a, …, a) = a.

Пример 4. Функция xy сохраняет 0, сохраняет 1. Функция x®y сохраняет 1 и не сохраняет 0.

2.6. Замыкание и замкнутые классы

Определение 1. Пусть MÍР₂. Замыканием М называется множество всех функций из P₂, которые можно выразить формулами над М. Замыкание М обозначается [M].

Определение 2.Множество функций М называется замкнутым классом, если [M]=M.

Пример 1.

1) P₂ – замкнутый класс.

2) Множество {1,x₁Åx₂} не является замкнутым классом. Его замыканием будет класс линейных функций: [{1, x₁ Å x₂}] = {f(x₁, ..., x_n) = c₀ Å c₁x₁ Å ... Å c_nx_n}. Действительно, по определению формулы над М, функция f(G₁, x₃), где f – есть сумма по модулю 2, G₁ – функция х₁ Å х₂, будет формулой над М: f(G₁, x₃) = (x₁ Å x₂) Å x₃.

Замечание.В терминах замыкания и замкнутого класса можно дать другое определение полноты, эквивалентное исходному:

М – полная система, если [M] = P₂.

3) A = {f(x₁, ..., x_n)| f(1, 1, ..., 1) = 0} – незамкнутый класс. Возьмем формулу над этим множеством. Пусть f, g₁, ..., g_n Î A, т.е. f(1, 1, ..., 1) = 0, g₁(1, 1, ..., 1) = 0, тогда f(g₁, ..., g_n) Î [A]. Посмотрим, принадлежит ли функция f(g₁, ..., g_n) множеству А. f(g₁(1, ..., 1), g₂(1, ..., 1), ..., g_n(1, ..., 1) = f(0, ..., 0)), но f(0, ..., 0) не обязано быть равным 0. Действительно, пусть g₁(x₁, x₂) = x₁ Å x₂, g₂(x) = x ÎA. Возьмем g₂(g₁(x₁, x₂)) = x₁ Å x₂ Î [A], g₂(g₁(1, 1)) = 1 Å 1 = 0, следовательно, g₂(g₁(x₁, x₂)) Ï A, отсюда [A] ¹ A и А – незамкнутый класс.

Важнейшие замкнутые классы в Р₂