рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Элементарные функции алгебры логики
Реферат Курсовая Конспект
Элементарные функции алгебры логики
Элементарные функции алгебры логики - раздел Образование, УСМАНОВА Зинира Масгутовна Обозначения: E2={0,1}; Е...
Обозначения: E2={0,1}; Е = E2´E2´...´E2 – прямое произведение n сомножителей; (x
= E2´E2´...´E2 – прямое произведение n сомножителей; (x ,..,xn)Î E2, | E2| – мощность E2, |E2|=2, тогда |Е
,..,xn)Î E2, | E2| – мощность E2, |E2|=2, тогда |Е |=2n.
|=2n.
Определение 1. Функцией алгебры логики называется закон, осуществляющий отображение Е
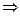 E2, причем отображение всюду определено и функционально.
E2, причем отображение всюду определено и функционально.
Так как множество Е конечно, то задать отображение Е
конечно, то задать отображение Е Þ E2, означает задать множество наборов из Е
Þ E2, означает задать множество наборов из Е и для каждого набора указать его образ в Е 2.
и для каждого набора указать его образ в Е 2.
Пример 1. Пусть n=2, тогда Е ={(0 0),(0 1),(1 0),(1 1)}, отображение Е
={(0 0),(0 1),(1 0),(1 1)}, отображение Е Þ E2 задано, например, так: (0 0) Þ0 ; (0 1) Þ1; (1 0) Þ1 ; (1 1) Þ1.
Þ E2 задано, например, так: (0 0) Þ0 ; (0 1) Þ1; (1 0) Þ1 ; (1 1) Þ1.
Тем самым задана функция, для которой мы будем использовать стандартное обозначение f(x1,x2), записывая эту функцию в виде таблицы:
| x1 | x2 | f(x1,x2) |
Здесь x1 и x2 обозначают названия столбцов, а f – символ, обозначающий отображение. Следует обратить внимание, что функции f(x1,x2) и f(y1,y2) задают одно и то же отображение, и их таблицы отличаются только названиями столбцов.
Определение 2.Таблица, задающая функцию f(x1,x2,...,xn), называется таблицей истинности для этой функции.
Рассмотрим функции одной переменной. Их будет всего 4, они задаются следующими таблицами истинности:
| x | f0(x) |
функция называется константой 0, записывается f0(x) 0;
0;
| x | f1(x) |
функция называется тождественной, записывается f1(x)= x;
| x | f2(x) |
функция называется «не x» и записывается f2 (x)=  ;
;

| x | f3(x) |
функция записывается f3(x) 1 и называется константой 1. Если стандартным расположением переменной x считать 0 в первой строке и 1 во второй, то функции f0, f1, f2, f3 определяются однозначно наборами значений: f0=(0,0), f1=(0,1), f2=(1,0) и f3=(1,1). Наборы значений функций составляют множество E2´Е2, поэтому количество функций одной переменной равно |E2
1 и называется константой 1. Если стандартным расположением переменной x считать 0 в первой строке и 1 во второй, то функции f0, f1, f2, f3 определяются однозначно наборами значений: f0=(0,0), f1=(0,1), f2=(1,0) и f3=(1,1). Наборы значений функций составляют множество E2´Е2, поэтому количество функций одной переменной равно |E2 E2|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.
E2|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.
Рассмотрим функции двух переменных f(x1,x2). Функции двух переменных определены на множестве Е ={(0 0),(0 1),(1 0),(1 1)}, эти наборы переменных из Е
={(0 0),(0 1),(1 0),(1 1)}, эти наборы переменных из Е можно тоже рассматривать как двоичные коды чисел 0,1,2,3, именно такой порядок расположения наборов (x1,x2) будем считать стандартным. Тогда функции f(x1,x2) определяются однозначно наборами значений (b1, b2, b3, b4), где каждое biÎE2, поэтому (b1, b2, b3, b4)ÎЕ
можно тоже рассматривать как двоичные коды чисел 0,1,2,3, именно такой порядок расположения наборов (x1,x2) будем считать стандартным. Тогда функции f(x1,x2) определяются однозначно наборами значений (b1, b2, b3, b4), где каждое biÎE2, поэтому (b1, b2, b3, b4)ÎЕ . Следовательно, число функций двух переменных равно 24=16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции.
. Следовательно, число функций двух переменных равно 24=16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции.
| x1 x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 0 0 1 1 0 1 1 |
Некоторые из этих функций носят специальные названия и играют такую же роль, как элементарные функции в анализе, поэтому называются элементарными функциями алгебры логики. Перечислим их.
1) f1(x1,x2) = (x1&x2), читается «конъюнкция х1 и х2», иногда вместо знака & употребляют знак  или вообще его опускают, пишут (х1х2). (х1&х2) совпадает с обычным произведением х1х2 и совпадает с min(x1,x2). Эту операцию называют также логическим умножением.
или вообще его опускают, пишут (х1х2). (х1&х2) совпадает с обычным произведением х1х2 и совпадает с min(x1,x2). Эту операцию называют также логическим умножением.
2) f6(x1,x2) = (x1Åx2) – сложение х1 и х2 по модулю два, иногда пишут (х1+х2)mod2.
3) f7(x1,x2) = (x1Úx2), читается «х1 дизъюнкция х2», она совпадает с max(x1,x2), ее называют логическим сложением.
4) f8(x1,x2) = (x1 x2), читается «х1 стрелка Пирса х2» и совпадает с отрицанием дизъюнкции, другие названия: функция Вебба, функция Даггера.
x2), читается «х1 стрелка Пирса х2» и совпадает с отрицанием дизъюнкции, другие названия: функция Вебба, функция Даггера.
5) f9(x1,x2) = (x1~x2), читается «х1 эквивалентно х2».
6) f13(x1,x2) =( x1 x2), читается «х1 импликация х2», иногда обозначается (х1Éх2), т. е. х1 влечет х2 .
x2), читается «х1 импликация х2», иногда обозначается (х1Éх2), т. е. х1 влечет х2 .
7) f14(x1,x2) = (x1|x2), читается «х1 штрих Шеффера х2», она является отрицанием конъюнкции.
Cимволы  ,&,Ú,
,&,Ú, ,~,
,~, ,Å,|, участвующие в обозначениях элементарных функций, называются логическими связками или просто связками. Переменные 0 и 1 называются логическими или булевыми переменными, причем 0 соответствует «лжи» , а 1 – «истине», а функции алгебры логики называются еще и блевыми функциями.
,Å,|, участвующие в обозначениях элементарных функций, называются логическими связками или просто связками. Переменные 0 и 1 называются логическими или булевыми переменными, причем 0 соответствует «лжи» , а 1 – «истине», а функции алгебры логики называются еще и блевыми функциями.
Рассмотрим функции f(x1...xn), где (x1...xn)Î Е , тогда число наборов (x1...xn),где функция f(x1...xn) должна быть задана, равно |Е
, тогда число наборов (x1...xn),где функция f(x1...xn) должна быть задана, равно |Е |=2n. Обозначим множество всех функций двузначной алгебры логики Р2. Обозначим через Р2(n) число функций, зависящих от n переменных. Очевидно, Р2(n)=22 n.
|=2n. Обозначим множество всех функций двузначной алгебры логики Р2. Обозначим через Р2(n) число функций, зависящих от n переменных. Очевидно, Р2(n)=22 n.
С ростом n число Р2(n) быстро растет: P2(1)=4, P2(2)=16, P2(3)=256, P2(4)=65536 . При больших n табличный способ задания функций становится неприемлемым, используется формульное задание функций. Но прежде чем ввести понятие формулы, дадим определение существенной переменной.
Определение 3. Функция f(x1,...,xi–1,xi,xi+1,...,xn) существенно зависит от хi, если существуют такие значения a1, ...ai–1, ai+1, ...an переменных x1, ...xi–1, xi+1, ...xn, что f(a1, ...ai–1, 0, ai+1...an)¹f(a1...ai–1, 1, ai+1...an) . Тогда переменная хi называется существенной переменной. В противном случае хi называется фиктивной переменной.
– Конец работы –
Эта тема принадлежит разделу:
УСМАНОВА Зинира Масгутовна
АХМЕТОВА Наиля Абдулхамитовна УСМАНОВА Зинира... Замыкание и замкнутые классы...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Элементарные функции алгебры логики
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов