рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Задачи и упражнения по функциям алгебры логики
Реферат Курсовая Конспект
Задачи и упражнения по функциям алгебры логики
Задачи и упражнения по функциям алгебры логики - раздел Образование, УСМАНОВА Зинира Масгутовна При Оперировании С Функциями Алгебры Логики Бывают Полезны Следующие Эквивале...
При оперировании с функциями алгебры логики бывают полезны следующие эквивалентности (большинство из них называют обычно основными эквивалентностями алгебры логики). Построив таблицу для соответствующих функций, убедитесь в справедливости следующих эквивалентностей:
1.  – коммутативность связки *, где символ * является общим обозначением для связок &, Ú, Å, ~, |, ¯.
– коммутативность связки *, где символ * является общим обозначением для связок &, Ú, Å, ~, |, ¯.
2.  – ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.
– ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.
3. Дистрибутивность
а)  – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;
б)  – дистрибутивность дизъюнкции относительно конъюнкции;
– дистрибутивность дизъюнкции относительно конъюнкции;
в)  – дистрибутивность конъюнкции относительно сложения по mod 2.
– дистрибутивность конъюнкции относительно сложения по mod 2.
4. а)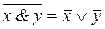 ; б)
; б) суть правила де Моргана;
суть правила де Моргана;
5. а) ; б)
; б) суть правила поглощения;
суть правила поглощения;
6. а) ; б)
; б) ;
;
7. а) ; б)
; б) ;
;
в)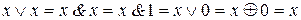 ; г)
; г) ; д)
; д) ;
;
8. а) ;
;
б) ; в)
; в) ;
;
9. а) ; б)
; б) .
.
1. Построить таблицы соответствующих функций, выяснить, эквивалентны ли формулы  и
и  :
:
1)  ,
,  ;
;
2)  ,
, 
3)  ,
,  ;
;
4)  ,
,  ;
;
5)  ,
, 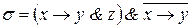 ;
;
6) 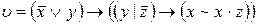 ,
,  ;
;
7)  ,
,  ;
;
8) 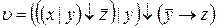 ,
,  ;
;
9)  ,
,  ;
;
10)  ,
,  .
.
Ответы: 2), 6), 9), 10) – эквивалентны; 3), 7) – не эквивалентны.
2. Построив таблицу для соответствующих функций, убедитесь в справедливости следующих эквивалентностей:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
10)  ;
;
11)  .
.
3. Используя приведенные выше основные эквивалентности и соотношения докажите эквивалентность формул V и U:
1) ,
,  ;
;
2) ,
,  ;
;
3) ,
, 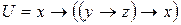 ;
;
4) ,
,  ;
;
5) ,
,  ;
;
6)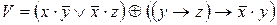 ,
,  ;
;
7) ,
,  ;
;
8) ,
, 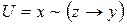 ;
;
9) ,
,  ;
;
10) ,
,  .
.
Ответы:
4)
 ;
;
9)

4. Используя непосредственно определение двойственности булевых функций, а также основные эквивалентности и соотношения, выясните, является ли функция g двойственной к функции f:
1) ,
,  ;
;
2) ,
,  ;
;
3)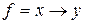 ,
, 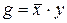 ;
;
4) ,
,  ;
;
5) ,
,  ;
;
6)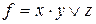 ,
,  ;
;
7) ,
,  ;
;
8) ,
,  ;
;
9) ,
, 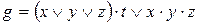 ;
;
10)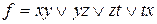 ,
,  ;
;
11) ,
,  ;
;
12) ,
,  .
.
Ответы: 4) ,
, 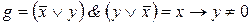 . Значит, g не двойственна к f. 6) – не является; 8),9),11) – является.
. Значит, g не двойственна к f. 6) – не является; 8),9),11) – является.
5. Используя принцип двойственности, постройте формулу, реализующую функцию, двойственную к функции f, и убедитесь в том, что полученная формула эквивалентна формуле V:
1) ,
,  ;
;
2) ,
, 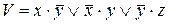 ;
;
3)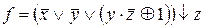 ,
,  ;
;
4) ,
,  ;
;
5) ,
,  ;
;
6) ,
,  ;
;
7) ,
,  ;
;
8) ,
,  ;
;
9)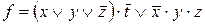 ,
,  ;
;
10) ,
, 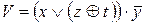 .
.
Ответы:
1)
2) ; 5)
; 5) ; 10)
; 10) .
.
6. Указать все фиктивные переменные у функции f:
1)
2)
3)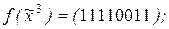
4)
5)
6)
Ответы:1)две фиктивные переменные; 3)одна фиктивная переменная; 5)фиктивные переменные x1 и x3.
7. Показать, что x1 – фиктивная переменная у функции f (реализовав для этой цели функцию f формулой, не содержащей явно переменную x1):
1) ;
;
2) ;
;
3) ;
;
4) 5)
5) 6)
6) 7)
7)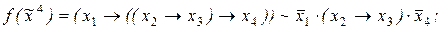
8) 9)
9) 10)
10)
Ответы: 4),8),10) 9)
9)
8. Выяснить, можно ли из функции f , отождествляя и переименовывая в ней переменные, получить функцию g:
1) ,
, 
2) ,
, 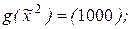
3) ,
, 
4) ,
, 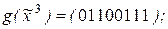
5)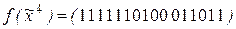 ,
, 
6) ,
, 
7) ,
,  ;
;
8) ,
,  ;
;
9) ,
, 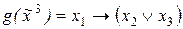 ;
;
10) ,
,  .
.
Ответы: 1),2),5),7),8),9),10)можно. 3),4),6)нельзя.
9. Представить в СДНФ следующие функции:
1) ;
;
2)
3)
4)
5)
6)
7)
8)
9)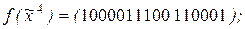
10)
Ответы: 2) ; 4)
; 4) , 7)
, 7)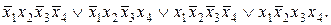
10. Представить в СКНФ следующие функции:
1)
2)
3)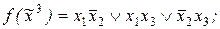
4)
5)
6)
7)
8)
9)
10)
Ответы: 1) ; 2)
; 2) ; 6)
; 6) ; 8)
; 8)
11. С помощью эквивалентных преобразований построить ДНФ функции
 :
:
1)
2)
3)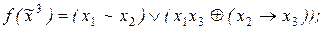
4)
5)
6)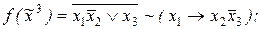
7)
8)
9)
10)
Ответы:
4)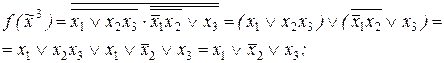
10)
12. Используя эквивалентные преобразования, построить КНФ функции
 :
:
1)



2)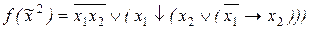 ;
;
3)


4)
5)
6)
7)
Ответы:
1)

3)
6)
13. Применяя преобразования вида 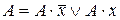 и
и построить из заданной ДНФ функции
построить из заданной ДНФ функции  ее совершенную ДНФ:
ее совершенную ДНФ:
1)
2)
3)
4)
5)
6)
7)
8)
Ответы:
2)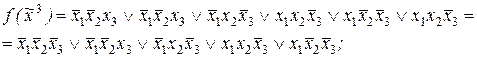
5)
14. С помощью преобразований вида  и
и  построить из данной КНФ функции
построить из данной КНФ функции  ее совершенную КНФ:
ее совершенную КНФ:
1)
2)
3)
4)
5)
6)
7)
8)
Ответы:
1)
5)
15. Используя дистрибутивный закон  и эквивалентности
и эквивалентности 
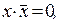

 и
и  перейти от заданной КНФ функции
перейти от заданной КНФ функции  к ДНФ:
к ДНФ:
1)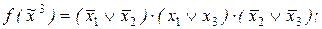
2)
3)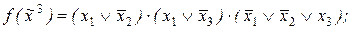
4)
5)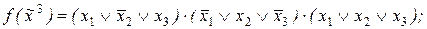
6)
7)
Ответы:
3)
6)
16. Используя дистрибутивный закон  и эквивалентности
и эквивалентности 


 и
и  перейти от заданной ДНФ функции
перейти от заданной ДНФ функции  к ее КНФ:
к ее КНФ:
1) 
2)
3)
4)
5)
6)
7)
8)
Ответы:
2)

5) 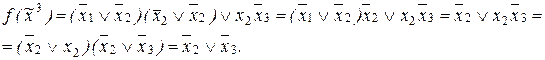
17. Методом неопределенных коэффициентов найти полиномы Жегалкина для следующих функций:
1)
2)
3)
4)
5)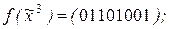
6)
7)
8)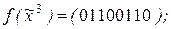
9)
10)
Ответы:
1)
 3)
3) 6)
6)
10)
18. Методом треугольника Паскаля построить полином Жегалкина для этой функции, если:
1) 2)
2)
3) 4)
4)
5) 6)
6)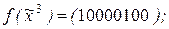
7) 8)
8)
9) 10)
10)
Ответы:
1) 4)
4) 7)
7)
19. Представив функцию  формулой над множеством связок {&,
формулой над множеством связок {&,  }, преобразуйте полученную формулу в полином Жегалкина функции
}, преобразуйте полученную формулу в полином Жегалкина функции  (используя эквивалентности
(используя эквивалентности 




 ):
):
1)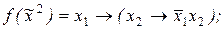
2)
3)
4)
5)
6)
7)
8)
9)
10)
Ответы:
1)
3)
9)
20. Построить множество всех функций, зависящих от переменных x1,x2 и принадлежащих замыканию множества А:
1) 
2)
3)
4)
5)
6)
7)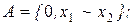
8)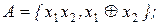
9)
10)
11)
12)
13)
14)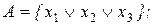
15)
Ответы: 1) 2)
2)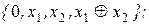 3)
3)
4) 5)
5) 6)
6)
21. Покажите, что  , выразив
, выразив  формулой над множеством А:
формулой над множеством А:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
Ответы: 1) 2)
2) 3)
3) 4)
4) 5)
5)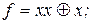 6)
6) 7)
7)

22. Выписать все попарно неконгруэнтные функции  , принадлежащие замыканию множества А:
, принадлежащие замыканию множества А:
1)  2)
2) 3)
3) 4)
4)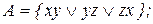
5) 6)
6) 7)
7) 8)
8) 9)
9)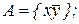 10)
10)
Ответы: 1) 2)
2) 3)
3) 4)
4)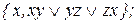 5)
5)
23. Из полной для класса [A] системы выделить базис:
1) 2)
2) 3)
3) 4)
4)
5) 6)
6)
7) 8)
8) 9)
9) 10)
10)
Ответы: 1) 2)
2) 3)
3)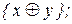 4)
4) 5)
5)
24. Сведением к заведомо полным системам в P2 показать, что множество А является полной системой в P2:
1)
2)
3)
4)
5)
6)
7)
8)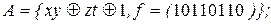
9)
10)
Ответы: 1)система  является полной в P2, поскольку всякая
является полной в P2, поскольку всякая  может быть представлена в виде ДНФ или КНФ. С другой стороны,
может быть представлена в виде ДНФ или КНФ. С другой стороны, 


2) имеем 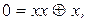

 Система
Система  полна, поскольку
полна, поскольку 
3) имеем  ;
;
4) имеем  ;
;
5) имеем  ;
;
25. Выяснить, является ли функция f самодвойственной:
1)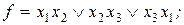
3)
5)
7)
2)
4)
6)
8)
9)
11)
13)
15)
10)
12) 14)
14)
Ответы: 1),3),4),8),10) – является; 2),5),6),7),9) – не является.
26. Выяснить, является ли самодвойственной функция f, заданная векторно:
1)
3) 
5)
7)
9)
11)
13)
15) 
2)
4)
6)
8)
10) 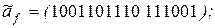
12)
14)
Ответы: 1),3),5),6),7),8) – является; 2),4),9),10) – не является.
27. Выяснить, является ли множество А самодвойственным:
1)
2)
3)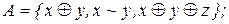
4)
5)
6)
7)
8)
9)
10)
11)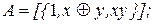
12)
13)
14)
15)
Ответы: 1),3),5-7),10) – является; 2),4),8),9) – не является.
28. Представив функцию f полиномом, выяснить, является ли она линейной:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)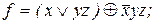
12)
13)
14)
15)
Ответы: 2),3),5),6),8),9)–является. 1),4),7),10)–не является.
29. Выяснить, является ли линейной функция f, заданная векторно:
1)
2)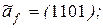
3)
4)
5)
6)
7)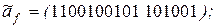
8)
9)
10)
11)
12)
13)
14)
15)
Ответы: 1),3),4),5),7),8),9),10) – является; 2),6) – не является.
30. Доказать, что система А полна в L. Выяснить, является ли система A базисом в L:
1)
2)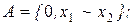
3)
4)
5)
6)
7)
8)
9)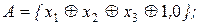
10)
11)
12)
13)
14)
15)
Ответы: 1)с помощью суперпозиции из функции  можно получить любую функцию вида
можно получить любую функцию вида  , путем подстановки 1-любую функцию вида
, путем подстановки 1-любую функцию вида 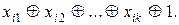 Система А является базисом;
Система А является базисом;
2),3),4),5),7),8),9) – является; 6),10) – не является.
31. Выяснить, принадлежит ли функция f множеству T1T0:
1)
– Конец работы –
Эта тема принадлежит разделу:
УСМАНОВА Зинира Масгутовна
АХМЕТОВА Наиля Абдулхамитовна УСМАНОВА Зинира... Замыкание и замкнутые классы...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Задачи и упражнения по функциям алгебры логики
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов