Основи теорії та методичні вказівки
Міністерство освіти і науки України
Чернігівський державний інститут економіки і управління
Затверджено радою
Обліково-економічного факультету
Протокол №1 від 28.08.2002 р.
КОМБІНАТОРИКА
Основи теорії та методичні вказівки
До виконання практичних завдань
ЕЛЕКТРОННИЙ ВАРІАНТ
Обговорено на засіданні кафедри ВМ та ЕММ
Протокол № 1 від 27.08. 2002 р.
Чернігів 2002
Вступ
Комбінаторика – важливий розділ математики, знання якого необхідні представникам різних спеціальностей. З комбінаторними задачами мають справу не лише математики, а й економісти, менеджери, соціологи. Комбінаторні методи лежать в основі розв’язання багатьох задач теорії ймовірностей.
Окремі комбінаторні задачі з’явилися дуже давно. У відомих тепер працях стародавніх індійських вчених знайдені формули числа перестановок і сполучень. В Європі елементи комбінаторики зустрічаються в працях Н. Тортальї (XVI ст.), але повної теорії перестановок, розміщень, сполучень він не дав. Перші теоретичні дослідження в цій галузі, у зв’язку з розвитком алгебри многочленів і виникненню теорії ймовірностей здійснили в XVII ст. французький математик Б. Паскаль (1623-1662) і П. Ферма (1601-1665). Ряд комбінаторних задач розв’язав Л. Ейлер (1707-1783). Проте в справжню математичну науку комбінаторика перетворилася лише в ХХ столітті, коли виникла потреба її застосування в обчислювальній техніці, кібернетиці, економіці й інших науках.
Сучасна комбінаторна математика сягає далеко за межі елементарної комбінаторики, знаходить широке застосування в багатьох дисциплінах.
В останні десятиріччя інтерес до комбінаторних задач значно посилився, оскільки виявилось, що багато важливих проблем, пов’язаних з розробкою оптимальних планів виробництва, транспортування, розміщення підприємств зводиться до задач комбінаторного характеру. Хоч ці задачі, як правило, досить складні вимагають надзвичайно великої кількості варіантів, сучасні комбінаторні методи пов’язані з застосуванням швидко діючих електронних обчислювальних машин, комп’ютерної техніки, дають можливість ефективно розв’язувати такі задачі.
Поняття комбінаторної задачі.
У практичному житті, серед різних математичних задач часто зустрічаються такі, в яких треба вибирати з деякої множини об'єктів підмножини елементів, які мають ті чи інші властивості, розміщувати їх у певному порядку за певними правилами знаходити число способів, за якими таке розташування можна здійснити. Наприклад, керівнику підприємства треба надіслати у відрядження певну групу спеціалістів, агроному розмістити сільськогосподарські культури на декількох полях і т.д.
Оскільки в таких задачах йдеться про ті чи інші варіанти, комбінації об'єктів, то їх називають комбінаторними задачами.
Розділ математики, в якому обґрунтовується теорія розв'язування комбінаторних задач, називається комбінаторикою.
Будь-яку комбінаторну задачу можна звести до задачі про скінченні множини, тому комбінаторику можна розглядати як складову частину теорії скінчених множин. Ми будемо вважати, що читач обізнаний з елементами теорії множин.
Спільним для всіх комбінаторних задач є те, що у кожній з них іде мова про деяку скінчену множину елементів і про кількість її підмножин, які задовольняють певні перелічені в умові вимоги умови.
Поряд з цим у різних комбінаторних задачах по різному підходять до поняття "рівні підмножини": в одних задачах підмножини, які відрізняються тільки порядком розташування в них елементів, треба вважати різними, а в інших порядок слідування елементів не істотний, і підмножини, які відрізняються тільки розташуванням елементів, не вважаються різними.
Якщо підмножини, які відрізняються тільки порядком слідування елементів, вважаються різними, то такі підмножини називаються упорядкованими.
Комбінаторні задачі поділяються на розміщення, перестановки і комбінації як без повторення, так 1 з повтореннями. У комбінаториці розроблені загальні методи і виведені готові формули для розв'язування комбінаторних задай, які ми далі розглянемо.
Оскільки в комбінаторних задачах мова йде про скінченні множини і їхні підмножини, то число способів комбінування елементів множин завжди виражається натуральним числом.
Загальні правила комбінаторики.
Правило суми. Якщо елемент а з множини А можна вибрати m способами, а елемент b множини В можна вибрати n способами, причому ніякий вибір a не збігається з жодним з виборів b , то число способів, якими можна здійснити хоча б один з цих виборів, дорівнює сумі m+n.
Правило суми легко узагальнюється.
Узагальнене правило суми. Нехай елемент а1 множини А1 можна вибрати m1 способами, елемент а2 множини А2 - m2 способами,..., елемент ak - множини Аk можна вибрати mk способами. Тоді число способів, якими можна здійснити хоча б один з цих виборів, дорівнює сумі m1 + m2 + ...+ mk .
Приклад 1. У спільному українсько-німецькому підприємстві працюють 100 робітників. З них 45 володіють англійською мовою, 65 – німецькою, 25 – англійською і німецькою мовами. Скільки працівників знають: а) хоча б одну мову?; б) тільки в одну мову; в) не знають жодної з них?
У спільному українсько-німецькому підприємстві працюють 100 робітників. З них 45 володіють англійською мовою, 65 – німецькою, 25 – англійською і німецькою мовами. Скільки працівників знають: а) хоча б одну мову?; б) тільки в одну мову; в) не знають жодної з них?
Розв'язання. U-множина працівників фірми
|
німецькою мовою, їх число N(В)=65.
Число працівників, що знають і англійську і німецьку є число елементів
перерізу множин А і В, тобто N (А∩В)=25. Тоді за правилом суми число
працівників які володіють хоч би однією мовою буде дорівнювати
N(A)+N(B)- N (А∩В),
тобто 45+65-25-85 (працівників). Отже, хоча б в однією мовою володіють 85 працівників.
б) Тільки англійською 45-25=20 (працівників), тільки німецькою 65-25=40 (працівників).
За правилом суми число студентів, що грають тільки в одну гру, дорівнює сумі 20+40=60 (студентів).
в) Не знають жодної з цих іноземних мов 100-85=15(працівників).
Відповідь. а) 85 працівників, б) 60 працівників, в) 15 працівників. Ілюстрація кругами Ейлера на рис.1.
Правило добутку. Якщо елемент а множини А можна вибрати m способами i при кожному а цих виборів елемент b множини В можна вибрати n способами, то упорядковану пару (а;b) можна вибрати m×n способами.
У справедливості правила добутку можна переконатись з таких міркувань. Нехай А=(а1,а2,…,аm) і В=(b1,b2,…,bm).
Тоді пари виду (а,b) можна записати у вигляді такої таблиці:
(а1;b1), (а1;b2),…, (а1;bn),
(а2;b1), (а2;b2),…, (а2;bn),
…………………………
(аm;b1), (аm;b2),…, (аm;bn).
Ця таблиця складається з m рядків, у кожному з яких міститься n елементів. Отже, загальне число пар дорівнює добутку m×n .
Множину впорядкованих пар, складених з елементів скінчених множин А і В, називають декартовим добутком цих множин і позначають АхВ.
Правило добутку легко узагальнюється на випадок кількох виборів.
Узагальнене правило добутку. Нехай елемент а1 з множини А1, можна вибрати m1 способами, елемент а2 з множини А2 - m2 способами,..., елемент аk з множини Ak можна вибрати mk способами.
Приклад 2. З Києва до Чернігова можна дістатися пароплавом, потягом, автобусом, літаком. З Чернігова до Новгород-Сіверського пароплавом і автобусом. Скількома способами можна здійснити подорож за маршрутом Київ-Чернігів-Новгород-Сіверський?
Розв'язання. Позначимо множину можливих способів подорожі від міста Києва до міста Чернігова через М, в ній чотири елементи, тому вибрати один елемент – спосіб подорожі, можна чотирма способами, тобто m=4. Множину можливих способів подорожі з міста Чернігова до міста Н.-Сіверський позначимо через Р, в ній 2 елементи, тому вибрати один елемент з цієї множини можна двома способами, тобто n=2.
Тоді за правилом добутку число способів вибору упорядкованої пари дорівнює добутку m×n=4×2=8. Отже, з міста Києва до міста Н.-Сіверського через місто Чернігів можна вибрати 8 способів подорожі.
3. Розміщення
Означення. Кожна упорядкована m-елементна підмножина n-елементної множини, називається розміщенням з n елементів по m елементів.
У комбінаторних задачах необхідно вміти підраховувати число всіх розміщень з n елементів по m елементів. Для позначення числа розміщень з n елементів по m елементів вживають… Зрозуміло, що=1, бо існує лише одна підмножина n-елементної множини, яка не містить елементів (порожня множина). У…Теорема 1. Число розміщень з n елементів по m елементів дорівнює добутку m послідовних натуральних чисел від n до n-m+1 включно, тобто
Доведення. Число розміщень з n елементів по m елементів дорівнює числу всіх m-елементних упорядкованих підмножин n-елементної множини. Перший… Після вибору перших двох елементів залишається n-2 можливостей вибору… Останній m-й елемент m-елементної упорядкованої підмножини n-елементної множини можна вибрати n-m+1 способом, оскільки…Означення. Розміщенням з повтореннями з n елементів по m елементів називається будь-який упорядкований m-елементний набір виду (а1,а2,…,аm), де а1,а2,…,аm - елементи множини М=(а1,а2,…,аn), в якому хоч би один елемент повторювався.
Число всіх розміщень з повтореннями з n елементів по m елементів позначають символом 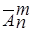 . На відміну від розміщень без повторень, де m£n, для розміщень з повтореннями може бути і m>n. Особливістю розміщень з повторенням е те, що після вибору першого елемента а1 (Мi, записавши його на першому місці набору, його повертають у множину М, тобто число елементів множини М залишається сталим для вибору другого, третього і т.д. m-го елемента набору. Повторивши цю операцію m разів, дістаємо деяке розміщення з повтореннями з n елементів по m елементів. Тому розміщення з повтореннями з n елементів по m елементів ще називають впорядкованими m-вибірками з n-елементної множини.
. На відміну від розміщень без повторень, де m£n, для розміщень з повтореннями може бути і m>n. Особливістю розміщень з повторенням е те, що після вибору першого елемента а1 (Мi, записавши його на першому місці набору, його повертають у множину М, тобто число елементів множини М залишається сталим для вибору другого, третього і т.д. m-го елемента набору. Повторивши цю операцію m разів, дістаємо деяке розміщення з повтореннями з n елементів по m елементів. Тому розміщення з повтореннями з n елементів по m елементів ще називають впорядкованими m-вибірками з n-елементної множини.
Теорема 2. Число розміщень з повтореннями з n елементів по m елементів обчислюють за формулою
де m і n - натуральні числа. Доведення. Перш за все відмітимо, що розміщення з повтореннями з n елементів… . (4)Перестановки.
Означення. Перестановками з n елементів називаються розміщення з n елементів по n елементів.
Число перестановок з n елементів позначають символом Рn (Р - перша буква французького слова реrmutation - перестановка). Оскільки за означенням Рn =, то формули для обчислення числа перестановок з n… Рn == n(n-1)(n-2)…3×2×1=n!Означення. Кожний упорядкований n-елементний набір з елементів множини М=(а1,а2,…,аk), - в якому елемент а1 повторюється n1 раз, елемент а2 повторюється n2 раз, i т.д., елемент аk повторюється nk раз, причому n1+n2+…+nk= n називається перестановкою з повтореннями з n nелементів.
Кількість усіх перестановок з повтореннями з n елементів, які відповідають означенню, позначають символом
Рn(n1,n2,…, nk),
де 1£k£n.
Теорема 4.Число Рn(n1,n2,…, nk),всіх перестановок довжиною n=n1+n2+…+nk з повтореннями з елементів а1,а2,…,аk, які повторюються відповідно n1,n2,…, nk раз, обчислюється за формулою
Рn(n1,n2,…, nk) =  (3)
(3)
Доведення. Кожна з перестановок містить n елементів. Якби всі елементи були різними, то мали б Рn=n!. Але оскільки не всі елементи різні, то ряд перестановок будуть однаковими. Зокрема без зміни елементи а1 можна переставляти між собою n1! способами, елемент а2=n2! способами і т.д,, елемент аk=nk! способами. Тому за правилом добутку в кожній перестановці з повтореннями можна переставляти елементи , не змінюючи перестановки n1!n2! … nk! способами. Отже,
Рn(n1,n2,…, nk) × n1!n2! … nk!=n!,
а звідси
Рn(n1,n2,…, nk) = 
Приклад 1. Абонент пам'ятає, що потрібний йому шестицифровий номер телефону починається з цифри 3 і містить три п'ятірки і дві дев'ятки. Проте розташування цифр він не пам'ятає. Скільки спроб повинен вробити абонент, щоб набрати потрібний номер?
Розв'язання. Маємо перестановки з повтореннями, всього спроб
буде

Відповідь. 10.
Приклад 2. Скількома способами можна розділити 10 акцій одного підприємства і 15 акцій іншого між п’ятьма особами?
Розв’язання. Використаємо метод перегородок. Спочатку з’ясуємо, скількома способами можна розділити 10 акцій одного підприємства між п’ятьма особами. Для цього добавимо до 10 акцій 4 перегородки, і розглянемо всі 14 елементів: 10 акцій і 4 перегородки. Кожній такій перестановці відповідає свій спосіб розподілу: перша особа отримує акції, що попали від початку зліва до першої перегородки, і друга – всі акції, що є між першою і другою перегородками і так далі. Отже, кількість розподілів 10 акцій між п’ятьма особами дорівнює числу перестановок з 14 елементів з повтореннями, тобто
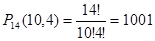
Аналогічно, кількість способів розподілу 15 акцій іншого підприємства між п’ятьма особами дорівнює числу перестановок з 19 елементів з повтореннями (15 акцій і 4перегородки), тобто


Тоді за правилом добутку, оскільки кожний з розподілів акцій першого підприємства можна комбінувати з кожним способом розподілу акцій двох підприємств між п’ятьма особами буде дорівнювати

Відповідь. 3879876 способів.
Сполучення.
Означення. Сполученням з n елементів по m елементів називають будь-яку m-елементну підмножину n-елементної множини.
Кількість всіх сполучень з n елементів по m елементів позначають символом (читають: "число комбінацій з n по m" або "це із n по m).… Для обчислення числа сполучень з n елементів по m елементів існує декілька…Теорема 5. Для довільних натуральних n i m (m£n) має місце формула
Доведення. Спочатку утворимо всі можливі неупорядковані m-елементні підмножини n-елементної множини, їх число дорівнює . Потім з кожної одержаної… =m!, а звідси =Теорема 6. Для довільних натуральних n і m (m£n) справджується рівність
Доведення. Рівність (3) безпосередньо випливає з формули (2). Справді, = Теорема 7. Для довільних натуральних m i n (m£n) справджується рівністьНаслідок 2. Число комбінацій з nелементів по m елементів виражається через: а) число розміщень в n елементів по m елементів формулою
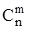 =
= -наслідок з (1);
-наслідок з (1);
Б) число перестановок формулою
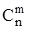 =
= - наслідок з (2).
- наслідок з (2).
Наслідок 3. Нехай множина М складається з двох елементів а і b. Тоді число перестановок з n елементів, в яких елемент а повторюється n-m разів, а елемент b повторюється m разів, дорівнює

 =
=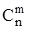 .
.
Отже, число комбінацій з n елементів по m дорівнює числу перестановок з повтореннями складу (n-m,m).
Приклад.1. Скількома способами можна вибрати з 20 осіб делегацію в складі 4 осіб?
Розв'язання. Різними вважатимемо ті делегації, які відрізняються хоча б одним членом. Кількість способів вибрати з 20 осіб делегацію в складі 4 осіб дорівнює числу комбінацій з 20 елементів по 4:
 =
=
Відповідь. 4845.
Приклад. Скількома способами збори акціонерів з 100 осіб можуть обрати президію з 5 осіб, у тому числі голову і секретаря?
Роз’язання:
1 спосіб. Кількість способів обрання голови і секретаря з 100 осіб дорівнює числу розміщень з 100 по 2 без повторень, тобто:

Кількість способів обрання ще трьох членів президії дорівнює числу сполучень з 98 осіб по три, тобто:

Всього кількість способів обрання президії дорівнює добутку

2 спосіб. Кількість способів обрання президії з 5 осіб на зборах, де присутні100, осіб дорівнює числу сполучень з 100 по 5 без повторень, тобто:

Потім президія з 5 осіб обирає з свого складу голову і секретаря. Кількість способів обрання голови і секретаря з 5 осіб дорівнює числу розміщень з 5 по 2 без повторень, тобто:

Всього кількість способів обрання президії дорівнює добутку

Відповідь. 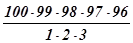
Означення. Сполученнямз повтореннями з n елементів по m елементів називається будь-який m-елементний набір виду (а1,а2,…,аm), де кожний з елементів а1,а2,…,аm належить до одного з n типів.
З означення випливає, що сполучення з повтореннями є не впо-рядкованими множинами, тому розташування елементів в наборах-множинах не має значення. Різні комбінації з повтореннями відрізняються одна від одної елементами, що до них входять, при цьому кожний елемент може входити в комбінацію декілька разів. Тому для сполучень з повтореннями може бути як m £n, так i n<m, на відміну від сполучень без повторень, де завжди m£п.
Наприклад, з двох елементів а і b можна скласти такі комбінації з повтореннями з двох елементів по три елементи (n<m):
ааa, ааb, bbа, bbb,
а з трьох елементів а, b, с по два елементи (n>m) такі:
аа, аb, ас, bb, bс, сс.
Оскільки комбінації з повтореннями є неупорядкованими множинами, то кожна така комбінація однозначно визначається тим, скільки елементів кожного типу в неї входить.
Наприклад, якщо маємо елементи трьох сортів, то комбінація з повтореннями з трьох елементів по п'ять елементів повністю визначається, якщо вказано, що вона містить два елементи першого типу, не містить жодного елемента другого типу і містить три елементи третього типу. Таку комбінацію можна умовно записати так (2,0,3); з цього запису видно, скільки елементів кожного типу входить в дану комбінацію. Запис іншої комбінації (1,2,2) показує, що в цю комбінацію входить один елемент першого типу і по два елементи другого і третього типів. Відмітимо, що в даному випадку кожна комбінація складається з п'яти елементів, що є сумою всіх елементів, що входять у комбінацію.
Кількість усіх комбінацій з n елементів по m елементів з повтореннями будемо позначати символом  . Для його знаходження користуються такою теоремою.
. Для його знаходження користуються такою теоремою.
Теорема 8. Число різних можливих сполучень з повтореннями і з n елементів по m елементів при довільних натуральних n іm обчислюється за формулою
Доведення. Сполучення з повтореннями з n елементів по m елементів можна записати, користуючись тільки цифрами 0 і 1. Це можна зробити так: спочатку… Впорядкована множина, складена з одиниць і нулів, відповідна сполученню з… ==Схема розв¢язання комбінаторних задач
Вибір правила
| Правило суми | Правило добутку |
| Якщо елемент А можна вибрати m способами, а після цього елемент В – n способами, тобто А або В можна вибрати (m+n) способами | Якщо елемент А можна вибрати n способами, а елемент В – n способами, то А і В можна вибрати (mn) способами |
Вибір формули

Варіанти індивідуальних завдань
Варіант 1 1. Розклад одного дня містить 4 різних пари. Знайти кількість можливих розкладів, якщо вивчається 9 дисциплін.Література.
1. Антонов Н.П. и др. Сборник задач по элементарной математике: Пособие для самообразования.-М.:Наука, 1967.-528с.
2. Боровик В.Н., Вивальнюк Л.М., Костарчук В.М., Шефтель З.Г. Математика: Посібник для педінститутів. - К,: Вища школа, 1980.-400с.
3. Боровик В.Н., Вивальнюк Л.М., Мурач М.М., Соколенко 0.І. Курс математики: Навчальний посібник для студентів педінститутів. - К.: Вища школа, 1995.- 392с.
4. Вивальнюк Л.М., Шефтель З.Г., Рафаловский Е.В. Математика: Посібник для факультативних занять у 9 класі. -К.: Рад. школа, 1984.- 136с.
5. Виленкин Н.Я. Комбинаторика.- М.: Наука, 1969.-328с.
6. Горделадзе Ш.Г., Кухарчук М.М.. Яремчук Ф.П. Збірник конкурсних задач з математики: Посібник для вступників до вузів. - К.: Вища школа, 1973.-324с.
7. Збірник задач з математики для вступників до вузів. За редакцією М.І.Сканаві.- К.: Вища школа, 1992.-446с.
8. Ігнатенко М.Я., Боровик В.Н. Метод математичної індукції.-Чернігів, 1995.-99с.
Зміст
| Вступ | |
| 1. Поняття комбінаторної задачі | |
| 2. Загальні правила комбінаторики | |
| 3. Розміщення | |
| 4. Перестановки | |
| 5. Сполучення | |
| 6. Схема розв’язання комбінаторних задач | |
| Варіанти індивідуальних завдань | |
| Література | |
| Зміст |