Задача о раскрое материалов.

На раскрой (распил, обработку) поступает материал одного образца в количестве А единиц. Требуется изготовить из него L разных комплектующих изделий в количествах, пропорциональных числам b1, b2, … b_l (условие комплектности). Каждая единица материала м.б. раскроена N различными способами, причем использование i-го способа (i=1,2,…,n) дает а_ik единиц k-го изделия (к=1,2, …,l).

Необходимо найти план раскроя, обеспечивающий макс число комплектов.

Составим ЭММ задачи:

Обозначим Хi – число единиц материала раскраиваемых i-ым способом, и Х – число изготавливаемых комплектов изделий. Т.к. общее количество материала равно сумме его единиц, раскраиваемых различными способами, то

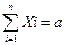(2.1)

Требование комплектности выразится уравнениями

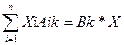(k=1,2,…, l) (2.2)

Очевидно, что Хi >= ) (i=1,2,…,n) (2.3)

 

ЭММ задачи: найти такое решение Х=(х1, х2, …, хn), удовлетворяющее системе уравнений (2.1) – (2.2) и условию (2.3), при котором функция F = х принимает макс значение.

Эту задачу можно обобщить на случай m раскраиваемых материалов.

Пусть каждая единица j-го материала (j = 1, 2,…, m) может быть раскроена N различными способами, причем использование i-го способа (i =1,2,…,n) дает а_ijk единиц k-го изделия (к=1,2, …,l), а запас j-го материала равен Aj единиц.

Обозначим Хij – число единиц j-го материала раскраиваемого i-ым способом.

ЭММ задачи о раскрое материалов в общей постановке примет вид: найти такое решение Х=(х11, х12, …, хnm), удовлетворяющее системе

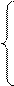
(j = 1, 2,…, m),

(k=1,2,…, l)

и условию Xij >= 0, при котором функция F = х принимает макс значение.

 

Рассмотренные примеры задач линейного программирования позволяют сформулировать общую задачу линейного программирования.

Дана система m линейных уравнений и неравенств с n переменными

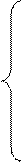а11*Х1 + а12*Х2 + … + а1n*Xn <= В1

а21*Х1 + а22*Х2 + … + а2n*Xn <= В2

………………………….

ак1*Х1 + ак2*Х2 + … + акn*Xn <= Вк

ак+1,1*Х1 + ак+1,2*Х2 + … + а к+1,n*Xn = В к+1 (1)

а к+2,1*Х1 + а к+2,2*Х2 + … + а к+2,n*Xn = В к+2

………………………….

аm1*Х1 + аm2*Х2 + … + аmn*Xn = Вm

 

и линейная функция

F = С1*Х1 + С2*Х2 + … + Сn*Xn (2)

 

Найти такое решение системы Х = (Х1, Х2, …,Xj,…, Хn), где

Хj>=0 (j = 1, 2,…, l; l<=n) (3)

при котором линейная функция F (2) принимает оптимальное (макс или мин) значение.

Система (1) называется системой ограничений, а функция F – линейной функцией, линейной формой, целевой функцией или функцией цели.

Более кратко общую задачу линейного программирования можно представить в виде:

F = 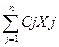à max (min)

При ограничениях:

(I = 1, 2, …, k)

(I = k+1, k+2, …, m)

Хj>=0 (j = 1, 2,…, l; l<=n)

 

Оптимальным решением (или оптимальным планом) задачи ЛП называется решение Х = (Х1, Х2, …,Xj,…, Хn) системы ограничений (1), при котором линейная функция (2) принимает оптимальное (макс или мин) значение.

Термины «решение» и «план» - синонимы, однако первый используется чаще, когда речь идет о формальной стороне задачи (ее математическом решении), а второй – о содержательной стороне (экономической интерпретации).

 

При условии, что все переменные неотрицательны (Хj>=0, j = 1, 2,…, n), система ограничений (1) состоит лишь из одних неравенств, - такая задача ЛП называется стандартной; если система ограничений (1) состоит из одних уравнений, то задача называется канонической. В приведенных выше примерах задача 1 – стандартная, 2 – каноническая. Бывает – общая.

Любая задача ЛП м.б. сведена к канонической, стандартной или общей.

 

Вспомогательная теорема (без доказательства):

Всякому решению неравенства

аi1*Х1 + аi2*Х2 + … + аin*Xn <= Вi (4)

соответствует определенное решение уравнения

аi1*Х1 + аi2*Х2 + … + аin*Xn + Хn+i= Вi (5)

в котором Хn+i>=0 I = 1,m (6)

 

и, наоборот, каждому решению уравнения (5) и неравенства (6) соответствует определенное решение неравенства (4).

Используя эту теорему, можно представить стандартную задачу (1.4) – (1.6) в каноническом виде. С этой целью в каждое из m неравенств в системе ограничений (1.4) вводятся дополнительные неотрицательные переменные Xn+1, Xn+2, Хn+m и система ограничений примет вид:

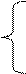а11*Х1 + а12*Х2 + … + а1n*Xn + Xn+1 = В1

а21*Х1 + а22*Х2 + … + а2n*Xn + Xn +2 = В2 …………………………………………………………….

аm1*Х1 + аm2*Х2 + … + аmn*Xn + Xn +m = Вm

 

Замечание. В рассматриваемой задаче все неравенства вида <=, поэтому дополнительные неотрицательные переменные вводились со знаком «+». В случае неравенства вида >= соответствующие дополнительные неотрицательные переменные вводились бы со знаком «-».