Инвариантность формы дифференциала
С правилом дифференцирования сложной функции связано свойство, которое называется:
Инвариантность формы дифференциала.
Пусть функции 
и 
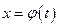таковы, что из них может быть составлена сложная функция: 
, и пусть существуют производные 
и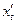 
. Тогда существует и производная 
.
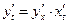Дифференциал функции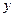 
как функции от независимой переменной 
выглядит следующим образом:
.
Если рассматривать функцию от независимой переменной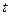 
, то дифференциал будет равен
.
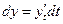Применив формулу для производной сложной функции, получим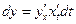 
.
Так как 
- дифференциал функции 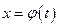, то мы снова приходим к формуле . Но здесь уже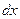 
не является приращением независимой переменной и в случае нелинейной функции 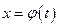не совпадает с приращением 
.
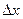Таким образом, видим, что форма дифференциала даже в том случае, если прежняя независимая переменная заменена новой.