Производная от сложной функции
Производная от сложной функции.
Покажем, что эта функция дифференцируема, и вычислим ее производную. Итак, фиксируем точку . Придадим переменной некоторое приращение , ему будут… , где - бесконечно малые функции при .Формула конечных приращений.
Тогда справедлива формула .Производная по заданному направлению.
. Определение. Производной функции по направлению в точке называется величина … .Градиент функции.
Из формулы для производной по направлению видим, что . Скалярное произведение будет максимальным, если векторы будут сонаправлены, то есть, если направление вектора будет…Инвариантность формы первого дифференциала.
Пусть функция 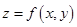 имеет непрерывные частные производные
имеет непрерывные частные производные 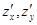 . Тогда она будет дифференцируема, а ее дифференциал имеет вид
. Тогда она будет дифференцируема, а ее дифференциал имеет вид 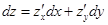 , где
, где 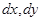 совпадают с приращениями переменных
совпадают с приращениями переменных  .
.
Пусть теперь переменные  в свою очередь являются функциями от новых переменных
в свою очередь являются функциями от новых переменных 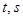 , причем функции
, причем функции 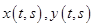 имеют непрерывные частные производные
имеют непрерывные частные производные 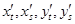 . Тогда функция
. Тогда функция 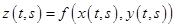 будет иметь непрерывные частные производные. Выпишем ее дифференциал в этом случае:
будет иметь непрерывные частные производные. Выпишем ее дифференциал в этом случае:
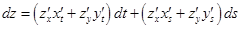
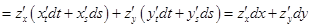 .
.
Видим, что дифференциал имеет прежнюю форму, только 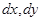 здесь уже не совпадают с приращениями переменных
здесь уже не совпадают с приращениями переменных  , а являются главными линейными частями этих приращений. Это свойство называется инвариантностью формы первого дифференциала.
, а являются главными линейными частями этих приращений. Это свойство называется инвариантностью формы первого дифференциала.