Раздел 2. Дифференциальное исчисление. Дифференциальные уравнения. Ряды
Раздел 2. Дифференциальное исчисление. Дифференциальные уравнения. Ряды.
Тема 5. Интегралы.
Лекция 14. Первообразная и неопределённый интеграл.
Первообразная
Восстановление функции по известной производной этой функции составляет одну из основных задач интегрального исчисления. Определение 1:Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений…Неопределённый интеграл.
При этом функция f(x) называется подынтегральной функцией,… Символ обозначает, таким образом, совокупность всех первообразных для функции f(x).Свойства неопределённого интеграла.
Свойство 1:Производная неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному… Свойство 2:Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной…Основные методы интегрирования.
2) Метод подстановки; 3) Метод интегрирования по частям.Таблица неопределённых интегралов некоторых функций.
1.) 
| 2.) 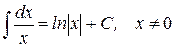
|
3.) 
| 4.) 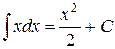
|
5.) 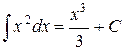
| 6.)
|
7.) 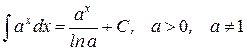
| 8.) 
|
9.) 
| 10.) 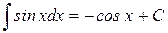
|
11.) 
| 12.) 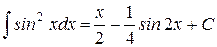
|
13.) 
| 14.) 
|
15.) 
| 16.) 
|
17.) 
| 18.) 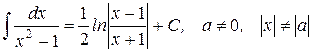
|
19.) 
| 20.) 
|
21.) 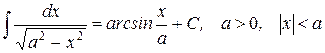
| 22.) 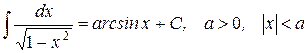
|
23.) 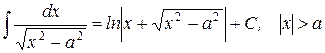
| 24.) 
|
25.) 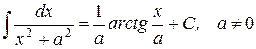
| 26.) 
|
27.) 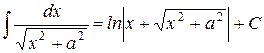
| 28.) 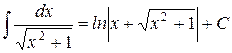
|
Основные свойства неопределённого интеграла.
Основные методы интегрирования.
Основные свойства определённого интеграла.
Формула Ньютона Лейбница.

Замена переменной в определённом интеграле:
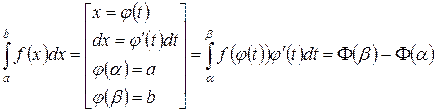
| Интегрирование по частям в определённом интеграле:
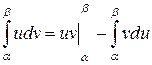
|
Лекция 1
Интегрирование рациональных функций.
Задача интегрирования рациональной функции сводится к нахождению интегралов следующих четырёх типов:Ответ:, где С=const
Интегрирование некоторых тригонометрических выражений.
Правило 1: Для вычисления интегралов вида:Тригонометрические подстановки.
Для подынтегральных выражений, содержащих радикалы, а также их квадраты удобны тригонометрические подстановки:

Интегралы вида .
Интегралы вида:
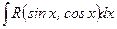
рационализируются подстановкой:

Некоторые интегралы, зависящие от радикалов.
Аналогично определяется рациональная функция трёх переменных R(x; y; z), четырёх и т.д. Интеграл видаПодстановки Эйлера.
рационализируются одной из подстановок Эйлера:Определённый интеграл.
Обозначим это разбиение через t, а точки x0, x1, x2, …, xn, будем называть точками разбиения. В каждом из полученных частичных отрезков [хi-1, хi]… Геометрический смысл суммы s: сумма площадей прямоугольников с основаниями… Определение 1:Если существует конечный предел I интегральной суммы при (l®0 – наибольшая из длин всех частичных…Основные свойства определённого интеграла.
· Если а>b, то ; · Каковы бы ни были числа а, b и с, всегда имеет место равенство: ; · Постоянный множитель можно выносить за знак определённого интеграла: ;Формула Ньютона Лейбница.
Замена переменной в определённом интеграле:Геометрические приложения определённого интеграла.
Площадь криволинейной трапеции:
· в прямоугольных координатах;
· в полярных координатах.
Объём тела вращения.
Несобственные интегралы.
Рассмотрим так называемые несобственные интегралы, то есть определённый… В таких интегралах сверх предельного перехода выполняется ещё один, то есть осуществляется двукратный переход к…Интеграл с бесконечным промежутком интегрирования
Пусть функция f(x) непрерывна на промежутке [а, +¥). Если существует конечный предел , то его называют несобственным интегралом первого рода и… Если интеграл имеет конечный предел, то говорят, что несобственный интеграл сходится;Интеграл функции, имеющей разрыв
Пусть функция f(x) имеет разрыв в точке х=b, а остальных точках этого промежутка (а; b) она непрерывна. Если существует конечный предел , то его… Аналогично определяется несобственный интеграл, когда функция f(x) имеет разрыв в точке х=а:Лекция 2
Понятие числового ряда.
называется числовым рядом или просто рядом. Числа а1, а2, а3, ..., аn ...… S1=а1, S2=а1+а2, S3=а1+а2+а3,…, Sn=а1+а2+а3+…+аn,Свойства сходящихся рядов.
Установлено, что сходящиеся ряды можно умножать на число, почленно складывать… · Если сходится ряд: и его сумма равна S, то и ряд где С=const, сходится и его сумма равна cS.Достаточные признаки сходимости положительных рядов
Признаки сравнения: · (сходимости) - Пусть даны два ряда с неотрицательными членами и и для всех… · (расходимости) - Пусть даны два ряда с неотрицательными членами и и для всех n выполняется неравенство . Тогда если…Знакопеременный ряд. Признак Лейбница
Признак Лейбница: Знакопеременный ряд сходится, если его члены стремятся к нулю всё время убывая по абсолютному значению. Итак, должны выполняться… 1) ; 2) .Абсолютная и условная сходимость
Остаток данного ряда (1) по абсолютному значению не превосходит соответствующего остатка ряда (2). Сумма S данного ряда(1) по абсолютному значению не превосходит суммы S' ряда…Ответ: ряд сходится.
· 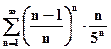
Применим признак Коши для положительного ряда:

Ответ: ряд сходится.
· 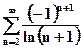
Применим признак Лейбница для знакопеременного ряда. Так как члены ряда стремятся к нулю всё время убывая по абсолютному значению, следовательно, ряд сходится:
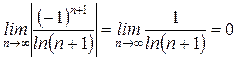
Ответ: ряд сходится.
Применим признак сравнения: Сравним данный ряд с рядом . Применяя интегральный признак сходимости, вычисляем интеграл:Ответ: ряд расходится.
Лекция 3
Степенной ряд.
а также ряд более общего вида (2): ао+а1(х-х0)+а2х2(х-х0) 2+...+апхп(х-х0) n+..., говорят, что он расположен соответственно по степеням х, о или по степеням х -… Постоянные а0, a1, ... , ап, ... называются коэффициентами степенного ряда.Промежуток и радиус сходимости степенного ряда, расположенного по степеням х
Теорема 1. Область сходимости степенного ряда есть некоторый промежуток (-R, R), симметричный относительно точки х=0. Иногда в него надо включить… Промежуток (-R, R) называется промежутком сходимости, положительное число R — радиусом сходимости степенного ряда.…Промежуток и радиус сходимости степенного ряда, расположенного по степеням х-а
Теорема 2. Радиус сходимости R степенного ряда, расположенногопо степеням х-а равен пределу отношения при условии, что этот предел (конечный или…Разложение функций в степенной ряд
Если функция f(x) разлагается в степенной ряд, то разложение единственно. Разложение простейших функций по степеням х: · показательные (2);Ряд Тейлора
Лекция 4
Дифференциальные уравнения. Основные понятия
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции (или нескольких неизвестных функций). Вместо производных могут содержаться дифференциалы.
Если неизвестные функции зависят от одного аргумента, то дифференциальное уравнение называется обыкновенным, если от нескольких, то уравнение называется дифференциальным уравнением с частными производными. Будем рассматривать только обыкновенные дифференциальные уравнения.
Общий вид дифференциального уравнения с одной неизвестной функцией таков:
F(х, у, у', у", ..., у(n)) = 0.
Порядком дифференциального уравнения называется порядок наивысшей из производных, входящих в это уравнение.
Функция у=j(х) называется решением дифференциального уравнения, если последнее обращается в тождество после подстановки у=j(х).
Основной задачей теории дифференциальных уравнений является нахождение всех решений данного дифференциального уравнения. В простейших случаях эта задача сводится к вычислению интеграла. Поэтому решение дифференциального уравнения называют также его интегралом, а процесс нахождения всех решений — интегрированием дифференциального уравнения.





 Вообще интегралом данного дифференциального уравнения называют всякое уравнение, не содержащее производных, из которого данное дифференциальное уравнение вытекает как следствие.
Вообще интегралом данного дифференциального уравнения называют всякое уравнение, не содержащее производных, из которого данное дифференциальное уравнение вытекает как следствие.
Дифференциальные уравнения первого порядка
Если уравнение можно разрешить относительно у', то оно принимает вид: y' = f(x,y) и называется уравнением первого порядка, разрешенным относительно… Дифференциальное уравнение удобно записать в виде: , являющемся частным… Уравнение в симметричной форме удобно тем, что переменные х и у в нем равноправны, т.е. каждую из них можно…ДУ I порядка. Уравнения с разделяющимися переменными
Если ДУ I имеет вид: Р(х)dx+Q(y)dy=0, в котором Р зависит только от х, а Q зависит только от у, то оно является ДУ I с разделёнными переменными.
Общий интеграл уравнения с разделёнными переменными представляется уравнением:
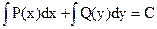
Если ДУ I имеет вид: X1Y1dy+X2Y2dx=0, в котором X1 и X2 зависят только от х, а Y1 и Y2 зависят только от у, то оно является ДУ I с разделяющимися переменными и приводится к ДУ I с разделёнными переменными. Процесс приведения называется разделением переменных.
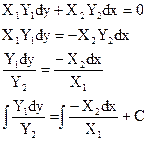
§93 Однородное ДУ I порядка (ОДУ I )
Пусть ДУ I имеет вид: Мdx+Ndy=0 – оно называется однородным ОДУ I, если отношение M/N можно представить как функцию отношения y/x. Это отношение обозначим через t:
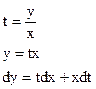
Тогда с помощью данной подстановки ОДУ I приводится к уравнению с разделяющимися переменными.
Лекция 5
§94 Линейное ДУ I порядка (ЛДУ I) Пусть ДУ I имеет вид: Мdx+Ndy=0 – оно называется ЛДУ I, если отношение M/N…Метод Бернулли.
y=u·v y¢=u¢·v+u·v¢ Подставляя выражения у и у¢ в заданное уравнение получаем:Метод Лагранжа (метод вариации постоянной).
Составим вспомогательное ЛОДУ I у¢+Р(x)у=0 и решим его как уравнение с разделяющимися переменными. То есть получим, что у=f(x)+C, где С=const –… Теперь будем искать общее решение заданного уравнения в виде у=f(x)+C(х), где… Найдём производную полученного выражения у¢ и подставим у и у¢ в заданное уравнение из которого выразим…Случаи понижения порядка
Иногда ДУ II или более высокого порядков допускает понижение порядка. Рассмотрим два случая:
Случай I: уравнение не содержит у.
Тогда в качестве неизвестной функции берётся величина у¢, а за аргумент принимаем х. При этом производные второго и высших порядков преобразуем по формулам:
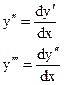
Случай II: уравнение не содержит х.
Тогда в качестве неизвестной функции берётся величина у¢, а за аргумент принимаем у. При этом производные второго и высших порядков преобразуем по формулам:

ЛДУ II
ЛДУ II называется уравнение вида: у²+Р(x)у¢+Q(x)у=R(x), где функции Р(х), Q(x), R(x) не зависят от х.
Если R(x)=0, то уравнение называется уравнением без правой части или однородным ЛОДУ II.
Если R(x)≠0, то уравнение называется уравнением с правой части или неоднородным ЛНДУ II.
ЛОДУ II с постоянными коэффициентами.
ау²+bу¢+cу=0, где а, b, c – некоторые постоянные. Составим характеристическое уравнение аk2+bk+c=0, которое в зависимости от D… · если D>0, то аk2+bk+c=0 имеет два различных действительных корня k1 и k2, тогда ЛОДУ II имеет общее решение…ЛНДУ II с постоянными коэффициентами.
ау²+bу¢+cу=R(x), где а, b, c – некоторые постоянные. Его общее решение имеет вид: , где - общее решение ЛОДУ II ау²+bу¢+cу=0;Свойства сходящихся рядов.
Сходящиеся ряды можно умножать на число, почленно складывать и вычитать так… · Если сходится ряд: и его сумма равна S, то и ряд где С=const, сходится и его сумма равна СS.Достаточные признаки сходимости положительных рядов
Признаки сравнения: · (сходимости) - Пусть даны два ряда с неотрицательными членами и и для всех… · (расходимости) - Пусть даны два ряда с неотрицательными членами и и для всех n выполняется неравенство . Тогда если…Знакопеременный ряд. Признак Лейбница
Признак Лейбница: Знакопеременный ряд сходится, если его члены стремятся к нулю всё время убывая по абсолютному значению. Итак, должны выполняться… 3) ; 4) .Степенной ряд.
а также ряд более общего вида (2): ао+а1(х-х0)+а2х2(х-х0) 2+...+апхп(х-х0) n+..., говорят, что он расположен соответственно по степеням х, или по степеням х -…Расположенного по степеням х
Теорема Область сходимости степенного ряда, расположенного по степеням х есть (-R, R), симметричный относительно точки х=0. Иногда в него надо… Промежуток (-R, R) называется промежутком сходимости, положительное число R — радиусом сходимости степенного ряда.…Расположенного по степеням х-а
Теорема Область сходимости степенного ряда, расположенного по степеням х-а есть некоторый промежуток (-R+а R+а), симметричный относительно точки…Дифференциальные уравнения первого порядка
Если уравнение можно разрешить относительно у', то оно принимает вид: y'=f(x, y) и называется уравнением первого порядка, разрешенным относительно… Дифференциальное уравнение удобно записать в виде: , являющемся частным… Уравнение в симметричной форме удобно тем, что переменные х и у в нем равноправны, т.е. каждую из них можно…Уравнения с разделяющимися переменными
Если ДУ−I имеет вид: Р(х)dx+Q(y)dy=0, в котором Р зависит только от х, а Q зависит только от у, то оно является ДУ−I с разделёнными переменными.
Общий интеграл уравнения с разделёнными переменными представляется уравнением:

Если ДУ−I имеет вид: X1Y1dy+X2Y2dx=0, в котором X1 и X2 зависят только от х, а Y1 и Y2 зависят только от у, то оно является ДУ−I с разделяющимися переменными и приводится к ДУ−I с разделёнными переменными. Процесс приведения называется разделением переменных.
Линейное ДУ−I порядка (ЛДУ−I)
Пусть ДУ−I имеет вид: Мdx+Ndy=0 – оно называется ЛДУ−I, если отношение M/N содержит у лишь в первой степени. ЛДУ−I принято записывать в виде у¢+Р(x)у=Q(x) где Р(x) и Q(x) непрерывные функции от х.
· Если Q(x)=0, то уравнение принимает вид у¢+Р(x)у=0 и оно называется ЛОДУ−I или линейным уравнением без правой части. В этом случае оно приводится к уравнению с разделяющимися переменными.
· Если Q(x)≠0, то уравнение называется ЛНДУ−I или линейным уравнением с правой части. В этом случае его можно решить методом Бернулли или методом Лагранжа.