рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Предел функции
Реферат Курсовая Конспект
Предел функции
Предел функции - раздел Математика, Предел функции При Вычислении Пределов Следует Помнить О Типовых Пределах, Которые Непосредс...
При вычислении пределов следует помнить о типовых пределах, которые непосредственно можно получить из определений соответствующих функций.
1.  , где f(x) – непрерывная в точке а функция, a – число.
, где f(x) – непрерывная в точке а функция, a – число.
2. 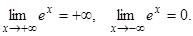
3. 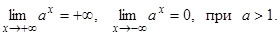
4. 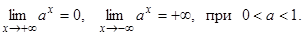
5. 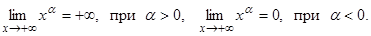
6. 
7. 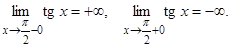
8. 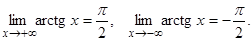
9. 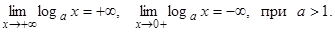
10. 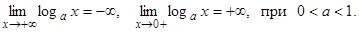
Непосредственное применение теорем о пределах не всегда приводит к цели. Например, нельзя применить теорему о пределе дроби, если ее знаменатель стремится к нулю. Так, если числитель и знаменатель дроби 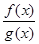 (при вычислении) одновременно стремятся к нулю или к бесконечности, тогда говорят, что дробь представляет собой неопределенность типа
(при вычислении) одновременно стремятся к нулю или к бесконечности, тогда говорят, что дробь представляет собой неопределенность типа 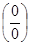 или
или 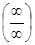 . Чтобы найти предел такой дроби, надо раскрыть неопределенность. Для раскрытия неопределенности существует несколько стандартных приемов.
. Чтобы найти предел такой дроби, надо раскрыть неопределенность. Для раскрытия неопределенности существует несколько стандартных приемов.
Пример 1. Вычислить 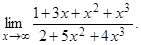
Решение. Применяя основные теоремы о пределах, имеем
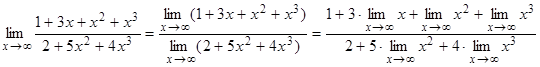 .
.
Видно, что данная дробь представляет собой неопределенность типа 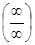 , для раскрытия этой неопределенности преобразуем данную дробь, разделив числитель и знаменатель на старшую степень многочлена, в данном примере на
, для раскрытия этой неопределенности преобразуем данную дробь, разделив числитель и знаменатель на старшую степень многочлена, в данном примере на 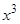 , от этого величина дроби не изменится:
, от этого величина дроби не изменится:
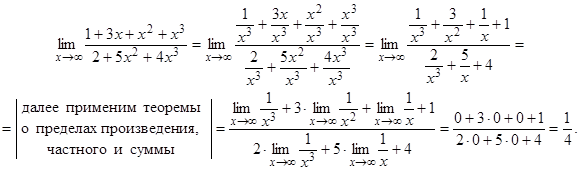
Таким образом, деление числителя и знаменателя дроби на старшую степень многочленов позволило от бесконечно больших величин перейти к бесконечно малым и тем самым раскрыть неопределенность.
Пример 2. Вычислить 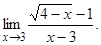
Решение. Непосредственное применение теорем о пределе дроби приведет к неопределенности типа 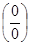 . Действительно, и числитель, и знаменатель стремятся к нулю при
. Действительно, и числитель, и знаменатель стремятся к нулю при  . Для раскрытия данной неопределенности избавимся от иррациональности в числителе дроби, для этого умножим числитель и знаменатель на выражение, сопряженное числителю, а именно на
. Для раскрытия данной неопределенности избавимся от иррациональности в числителе дроби, для этого умножим числитель и знаменатель на выражение, сопряженное числителю, а именно на 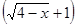 , в результате чего получим:
, в результате чего получим:
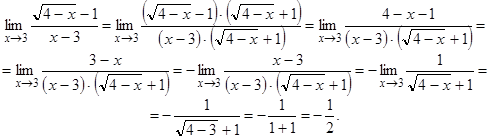
Итак, при наличии в дроби иррациональности (если дробь представляет собой неопределенность типа 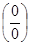 ), умножив числитель и знаменатель на сопряженное выражение, раскроем неопределенность.
), умножив числитель и знаменатель на сопряженное выражение, раскроем неопределенность.
Раскрытие неопределенности типа 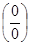 возможно осуществлять и с помощью первого замечательного предела:
возможно осуществлять и с помощью первого замечательного предела: 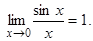
Пример 3. Вычислить 
Решение. Если подставить предельное значение, получим неопределенность типа 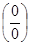 . Применив формулы тригонометрии, преобразуем числитель и знаменатель дроби:
. Применив формулы тригонометрии, преобразуем числитель и знаменатель дроби: 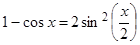 ,
, 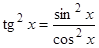 , тогда
, тогда
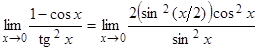 .
.
Умножим и числитель, и знаменатель на 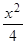 , получим:
, получим:
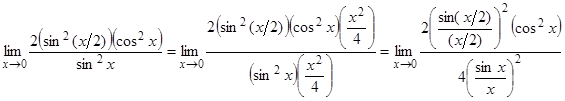 .
.
Согласно первому замечательному пределу получим:
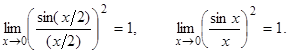
Следовательно, 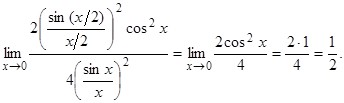
Отметим, что при применении первого замечательного предела, бесконечно малая величина, стоящая под знаком синуса и в знаменателе должна быть одна и та же.
Помимо неопределенности типа 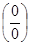 и
и 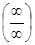 , существуют неопределенности типа:
, существуют неопределенности типа: 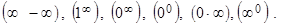
Для раскрытия неопределенности 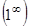 используют второй замечательный предел в одной из формулировок:
используют второй замечательный предел в одной из формулировок:
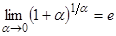 ,
, 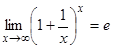 .
.
Пример 4. Вычислить следующие пределы:
а) 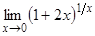 ; б)
; б) 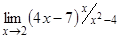 .
.
а) 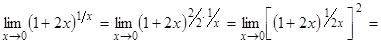
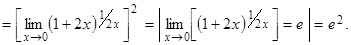
б) Подставляя предельное значение, получаем неопределенность типа 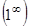 , преобразовав выражение под знаком предела, раскроем неопределенность. Для этого к выражению, стоящему в скобках, прибавим единицу и вычтем единицу. От этого выражение не изменится. Показатель степени умножим и разделим на
, преобразовав выражение под знаком предела, раскроем неопределенность. Для этого к выражению, стоящему в скобках, прибавим единицу и вычтем единицу. От этого выражение не изменится. Показатель степени умножим и разделим на 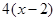 , получим:
, получим:
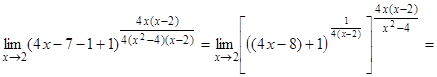
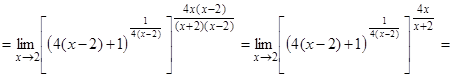
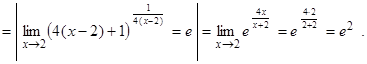
– Конец работы –
Эта тема принадлежит разделу:
Предел функции
Производная функции Основные правила нахождения производной где...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Предел функции
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов