Скалярное поле
Лекция №18
Элементы теории поля
Скалярное поле.
Поле называется скалярным, если «И» скалярная величина. Если выбрана некоторая декартова система координат, то задание скалярного поля эквивалентно…Поверхности уровня, линии уровня
Замечание:дляплоского поля уравнение определяет линии уровня. Для построения линий уровня соответствующих поверхностей в среде Matlab… contour(X,Y,Z) – строит линии уровня для поверхности Z =Z(X,Y),Производная по направлению.
Производная скалярного поля по направлению ℓ, заданному вектором , вычисляется по формуле , где Абсолютное значение производной о направлению определяет скорость изменения… Пример 2. Найти производную от функции в точке в направлении, идущем от этой точки к точке .Градиент.
Определение: Градиентом дифференцируемой функции) называется вектор , направленный по нормали к поверхности уровня поля в сторону возрастания поля,…Вычисление градиента функции
FX = gradient(F) — возвращает градиент функции одной переменной, заданной вектором ее значений F. FX соответствует конечным разностям в направлении… [FX.FY] = gradient(F) — возвращает градиент функции F(X,Y) двух переменных,… [FX.FY.FZ,...] = gradient(F) — возвращает ряд компонентов градиента функции нескольких переменных, заданной в виде…Графики поля градиентов quiver
· quiver(X.Y.U.V) — строит график поля градиентов в виде стрелок для каждой пары элементов массивов X и Y, причем элементы массивов U и V указывают… · qui ver(U, V) — строит векторы скорости в равнорасположенных точках на… · quiver(U,V,S) или quiver(X,Y.U,V,S) — автоматически масштабирует стрелки по сетке и затем вытягивает их по значению…Векторное поле.
Конкретными физическими примерами векторных полей являются: поле скоростей текущей жидкости, силовые поля (поле тяготения, электрическое и…Векторные линии.
Определение. Векторной линией векторного поля называется линия, в каждой точке которой касательная совпадает с вектором соответствующим этой точке.
Чтобы изучить определённое векторное поле, изучают расположение векторных линий.
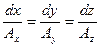 - это система дифференциальных уравнений семейства векторных линий поля
- это система дифференциальных уравнений семейства векторных линий поля 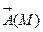 .
.
Дивергенция (расходимость) векторного поля
Основные свойства дивергенции: 1. , - произвольные постоянные. 2. .Поток вектора.
Возьмём в этом поле некоторую двухстороннюю поверхность S и выберем на ней определённую сторону, указав направление нормали к поверхности. Определение. Потоком (К) вектора через поверхность S называется интеграл по… Т.к. , то формулу можно записатьФизическая интерпретация
Пусть движение несжимаемой жидкости единичной плотности в пространстве задано векторным полем скорости течения 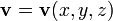 . Тогда масса жидкости, которая протечёт за единицу времени через поверхность S будет равна потоку векторного поля
. Тогда масса жидкости, которая протечёт за единицу времени через поверхность S будет равна потоку векторного поля 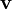 через поверхность S.
через поверхность S.
Ротор (вихрь) векторного поля.
. Основные свойстваротора: 1. , - произвольные постоянные.Циркуляция
Так как при затвердевании стенок канала нормальная к контуру компонента скорости будет погашена, жидкость по каналу будет двигаться с тангенциальной… где dl — элемент длины контура. Определение. Циркуляцией векторного поля называется криволинейный интеграл второго рода, взятый по произвольному…Свойства циркуляции
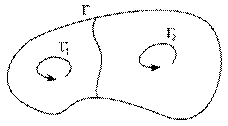
Свойство аддитивности циркуляции: циркуляция по контуру Γ есть сумма циркуляций по контурам Γ1 и Γ2, то есть C = C1 + C2
Формула Стокса
— Ротор (вихрь) вектора F. В случае, если контур плоский, например лежит в плоскости OXY, справедлива… ,где int Г— плоскость, ограничиваемая контуромОператор Гамильтона и векторные дифференциальные операции второго порядка.
Оператор Гамильтона (Оператор набла) - это векторный дифференциальный оператор, который в декартовых координатах определяется формулой:
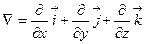
Сам вектор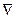 не имеет реального значения, он приобретает определённый смысл лишь в комбинации со скалярными или векторными функциями.
не имеет реального значения, он приобретает определённый смысл лишь в комбинации со скалярными или векторными функциями.
Представим grad, div и rot через оператор набла:
1. Произведение вектора 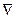 на скалярную функцию
на скалярную функцию 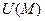 даёт градиент этой функции
даёт градиент этой функции
 .
.
2. Скалярное произведение вектора 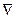 на векторную функцию
на векторную функцию 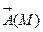 даёт дивергенцию этой функции
даёт дивергенцию этой функции
 .
.
3. Векторное произведение вектора 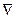 на векторную функцию
на векторную функцию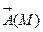 даёт ротор этой функции
даёт ротор этой функции
 .
.
Действия взятия градиента, дивергенции, ротора называются векторными дифференциальными операциями первого порядка, т.к. в них участвуют только первые производные.
В приложениях встречаются векторные дифференциальные операции второго порядка.
Оператор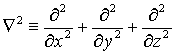 называется оператор Лапласа в декартовых координатах.
называется оператор Лапласа в декартовых координатах.
Дифференциальные операторы второго порядка: 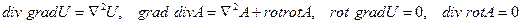
Интегральные теоремы
Теорема о градиенте 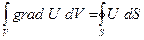
Теорема о дивергенции 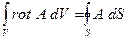
Теорема о роторе 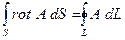

Пример применения MATLAB
Задача.
Дано: В объёме тетраэдра скалярное и векторное поля изменяются по линейному закону. Координаты вершин тетраэдра заданы матрицей вида [x1, y1, z1; x2, y2, z2; x3, y3, z3; x4, y4, z4]. Значения скалярного поля в вершинах заданы матрицей [Ф1; Ф2; Ф3; Ф4]. Декартовы компоненты векторного поля в вершинах заданы матрицей [F1x, F1y, F1z; F2x, F2y, F2z; F3x, F3y, F3z; F4x, F4y, F4z].
Определить в объёме тетраэдра градиент скалярного поля, а также дивергенцию и ротор векторного поля. Составить для этого функцию MATLAB.
Решение. Ниже приведён текст m-функции.
% grad_div_rot - Вычисление градиента, дивергенции и ротора ... в объёме тетраэдра
% [grad,div,rot]=grad_div_rot(nodes,scalar,vector)
% ВХОДНЫЕ ПАРАМЕТРЫ
% nodes - матрица координат вершин тетраэдра:
% строкам соответствуют вершины, столбцам - координаты;
% scalar - столбцовая матрица значений скалярного поля в вершинах;
% vector - матрица компонентов векторного поля в вершинах:
% строкам соответствуют вершины, столбцам - декартовы компоненты.
% ВЫХОДНЫЕ ПАРАМЕТРЫ
% grad - матрица-строка декартовых компонентов градиента скалярного поля;
% div - значение дивергенции векторного поля в объёме тетраэдра;
% rot - матрица-строка декартовых компонентов ротора векторного поля.
%
% При вычислениях предполагается, что в объёме тетраэдра
% векторное и скалярное поля изменяются в пространстве по линейному закону.
function [grad,div,rot]=grad_div_rot(nodes,scalar,vector);
a=inv([ones(4,1) nodes]); % Матрица коэффициентов линейной интерполяции
grad=(a(2:end,:)*scalar).'; % Компоненты градиента скалярного поля
div=[a(2,:) a(3,:) a(4,:)]*vector(:); % Дивергенция векторного поля
rot=sum(cross(a(2:end,:),vector.'),2).';
Пример запуска разработанной m-функции:
>> nodes=10*rand(4,3)
nodes =3.5287 2.0277 1.9881 8.1317 1.9872 0.15274 0.098613 6.0379 7.4679 1.3889 2.7219 4.451
>> scalar=rand(4,1)
scalar = 0.93181 0.46599 0.41865 0.84622
>> vector=rand(4,3)
vector = 0.52515 0.01964 0.50281 0.20265 0.68128 0.70947 0.67214 0.37948 0.42889
0.83812 0.8318 0.30462
>> [grad,div,rot]=grad_div_rot(nodes,scalar,vector)
grad = -0.16983 -0.03922 -0.17125
div = -1.0112
rot = -0.91808 0.20057 0.78844
Если предположить, что пространственные координаты измеряются в метрах, а векторное и скалярное поля - безразмерные, то в данном примере получилось:
grad Ф = (-0.16983*1x - 0.03922*1y - 0.17125*1z) м-1;
div F = -1.0112 м-1;
rot F = (-0.91808*1x + 0.20057*1y + 0.78844*1z) м-1.