Определение геометрического вектора. Линейные операциисложение, умножение на число над векторами и их свойства
Ответы на экзаменационные вопросы по векторной алебре
Определение геометрического вектора. Линейные операции(сложение, умножение на число) над векторами и их свойства.
Вектор представляет собой геометрический объект, характеризуемый длиной и направлением.
- Сложение векторов
Пусть даны два вектора 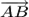 и
и 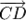 . Приложим вектор
. Приложим вектор 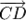 к точке
к точке 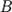 (концу вектора
(концу вектора 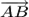 ) и получим вектор
) и получим вектор 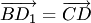 (рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор
(рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор 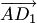 называется суммой векторов
называется суммой векторов
- Вычитание векторов
Вектор 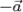 называется противоположным вектору
называется противоположным вектору 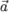 , если их сумма равна нулевому вектору:
, если их сумма равна нулевому вектору: 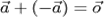 . Противоположный вектор
. Противоположный вектор 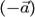 имеет длину
имеет длину 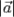 , коллинеарен и противоположно направлен вектору
, коллинеарен и противоположно направлен вектору 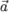 . Нулевой вектор является противоположным самому себе.
. Нулевой вектор является противоположным самому себе.
- Умножение вектора на число
Произведением ненулевого вектора а на действительное число 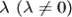 называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) длина вектора  равна
равна  , т.е.
, т.е.  ;
;
2) векторы  и
и 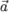 коллинеарные
коллинеарные 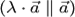 ;
;
3) векторы  и
и 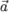 одинаково направлены, если
одинаково направлены, если  , и противоположно направлены, если
, и противоположно направлены, если  .
.
Произведение нулевого вектора на любое число 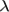 считается (по определению) нулевым вектором:
считается (по определению) нулевым вектором: 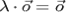 ; произведение любого вектора на число нуль также считается нулевым вектором:
; произведение любого вектора на число нуль также считается нулевым вектором: 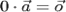 . Из определения произведения следует, что:
. Из определения произведения следует, что:
а) при умножении на единицу  вектор не изменяется:
вектор не изменяется: 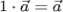 ;
;
б) при умножении вектора на 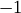 получается противоположный вектор:
получается противоположный вектор: 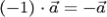 ;
;
в) деление вектора на отличное от нуля число 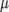 сводится к его умножению на число
сводится к его умножению на число 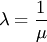 , обратное
, обратное 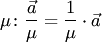 .
.
г) при делении ненулевого вектора 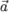 на его длину, т.е. при умножении
на его длину, т.е. при умножении 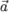 на число
на число 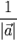 получаем единичный вектор, одинаково направленный с вектором
получаем единичный вектор, одинаково направленный с вектором 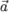 .
.
Действительно, длина вектора 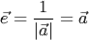 равна единице:
равна единице: 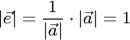 .
.
Вектор  коллинеарен и одинаково направлен с вектором
коллинеарен и одинаково направлен с вектором 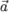 , так как;
, так как; 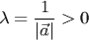
д) при умножении единичного вектора на число 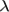 получаем коллинеарный ему вектор, длина которого равна
получаем коллинеарный ему вектор, длина которого равна 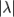 .
.
- Свойства линейных операций над векторами

Линейные комбинации векторов. Коллинеарность двух векторов. Компланарность трех векторов. Линейная зависимость компланарных векторов. Линейная зависимость четырех векторов в пространстве.
Линейные комбинации векторов
Вектор называется линейной комбинацией векторов , если он может быть представлен в виде где — некоторые числа. В этом случае говорят, что вектор разложен по векторам , а числа называют коэффициентами…Коллинеарность
Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой
Компланарность
Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости
Скалярное произведение векторов, его свойства.
Скалярное произведение векторов и : где - угол между векторами и ; если либо , тоБазис векторов на плоскости и в пространстве. Ортонормированный базис.
Числа x и y называются координатами вектора. Векторы и называются базисом… Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке (рис.1.32). Эти векторы…Проекция вектора на направление другого вектора
. В координатной форме формула для проекции примет вид .7)
Определители 2-го и 3-го порядка. Их определение и вычисление. Правило Саррюса
(1). Число называется определителем второго порядка, соответствующего таблице (1).… .Векторное произведение векторов. Определение и свойства. Линейность векторного произведения по сомножителям. Векторное произведение в декартовых прямоугольных координатах. Вычисление площади параллелограмма
Векторным произведением вектора 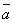 на вектор
на вектор 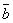 называется вектор, обозначаемый символом
называется вектор, обозначаемый символом 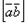 и определяемый следующими тремя условиями:
и определяемый следующими тремя условиями:
1). Модуль вектора 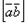 равен
равен 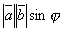 , где
, где 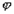 - угол между векторами
- угол между векторами 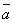 и
и 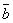 ;
;
2). Вектор 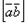 перпендикулярен к каждому из вектора
перпендикулярен к каждому из вектора 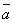 и
и 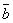 ;
;
3). Направление вектора 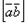 соответствует «правилу правой руки». Это означает, что если векторы
соответствует «правилу правой руки». Это означает, что если векторы 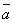 ,
, 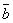 и
и 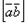 приведены к общему началу, то вектор
приведены к общему началу, то вектор 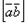 должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору
должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору 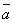 ), а указательный - по второму (то есть по вектору
), а указательный - по второму (то есть по вектору 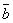 ).
).
Векторное произведение зависит от порядка сомножителей, именно:
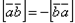 .
.
Модуль векторного произведения 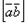 равен площади S параллелограмма, построенного на векторах
равен площади S параллелограмма, построенного на векторах 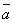 и
и 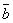 :
:
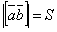 .
.
Само векторное произведение может быть выражено формулой
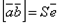 ,
,
где 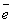 - орт векторного произведения.
- орт векторного произведения.
Векторное произведение 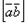 обращается в нуль тогда и только тогда, когда векторы
обращается в нуль тогда и только тогда, когда векторы 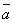 и
и 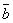 коллинеарны. В частности,
коллинеарны. В частности, 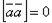 .
.
Если система координатных осей правая и векторы 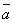 и
и 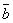 заданы в этой системе своими координатами:
заданы в этой системе своими координатами:
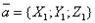 ,
,  ,
,
то векторное произведение вектора 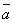 на вектор
на вектор 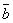 определяется формулой
определяется формулой
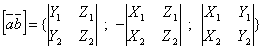 ,
,
или
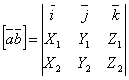 .
.
