Раздел 1. Линейная алгебра
Раздел 1. Линейная алгебра
Тема 1.1 Матрицы и определители
Матрицы и действия над ними Прямоугольной матрицей размера m x n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы,…Тема 1.2 Системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система видаРаздел 2. Математический анализ
Тема 2.2 Пределы и непрерывность
Предел последовательности Число a называется пределом последовательности x = {xn}, если для… Если число a есть предел последовательности x = {xn}, то говорят, что xn стремится к a, и пишут .Раздел 3. Дифференциальное исчисление
Тема 3.1 Производная функции
Производной функции f(x) в точке х = х0 называется предел отношения приращения…Тема 3.2 Приложение производной
Ключевые понятия: возрастание, убывание функции, экстремумы функции; выпуклость, вогнутость функции, точки перегибы; асимптоты; исследование функции с помощью производных высших порядков.
1. Возрастание и убывание функций
Теорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f¢(x) ³ 0.
2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f¢(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].
Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f¢(x)£0 на этом отрезке. Если f¢(x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b].
Конечно, данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).
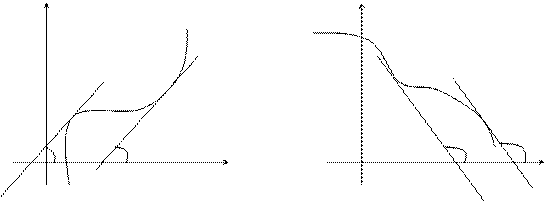Доказанную выше теорему можно проиллюстрировать геометрически:
y y
j j j j
x x
2. Точки экстремума.
Определение. Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 +Dx) > f(x2) при любом Dх (Dх может быть и отрицательным).
Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
Определение. Точки максимума и минимума функции называются точками экстремума.
Следствие. Обратное утверждение неверно. Если производная функции в некоторой… Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна…Раздел 4. Интегральное исчисление
Тема 4.1 Неопределенный интеграл
Первообразная функция. Определение: Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого…Тема 4.2 Определенный интеграл
Введение понятия определённого интеграла. Пусть на отрезке [a, b] задана непрерывная функция f(x).Раздел 5. Комплексные числа
Ключевые понятия: понятие комплексного числа, арифметические операции над комплексными числами, формы записи комплексного числа (алгебраическая, тригонометрическая), формула Муавра, переход от алгебраической формы в тригонометрическую и наоборот.
Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:
1) два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 = x2 и y1 = y2;
2) суммой комплексных чисел z1 и z2 называется комплексное число z вида
z = (x1 + x2, y1 + y2);
3) произведением комплексных чисел z1 и z2 называется комплексное число
z = (x1x2 - y1y2, x1y2 + x2y1);
4) множество комплексных чисел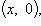 
, отождествляется с множеством действительных чисел R.
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 + z = z1, откуда находим z = z1 - z2 = (x1 - x2, y1 - y2).
Частным комплексных чисел z1 и z2 называется комплексное число z такое, что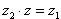 
. Отсюда находим
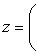
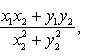
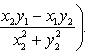
Комплексное число (0, 1) обозначается символом i = (0, 1). Тогда 
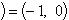, т. е. i2 = -1. Произвольное комплексное число z можно записать в виде
z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.
Эта запись называется алгебраической формой комплексного числа. Комплексное число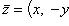 
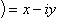называется сопряженным по отношению к комплексному числу z = (x, y) = x + iy.