рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Вид работы: Контрольные Работы
- /
- В а р и а н т 3
Реферат Курсовая Конспект
В а р и а н т 3
В а р и а н т 3 - Контрольная Работа, раздел Математика, АЛГЕБРА 9 КЛАСС 1. А) Х2 – 12Х + 35 = (Х – 5) (Х – 7);...
1. а) х2 – 12х + 35 = (х – 5) (х – 7);
х2 – 12х + 35 = 0;
х1 = 5, х2 = 7.
б) 7у2 + 19у – 6 = 7 (у – 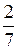 ) (у + 3) = (7у – 2) (у + 3);
) (у + 3) = (7у – 2) (у + 3);
7у2 + 19у – 6 = 0;
D = 361 + 168 = 529;
у1, 2 =  ;
;
у1 = 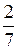 , у2 = –3.
, у2 = –3.
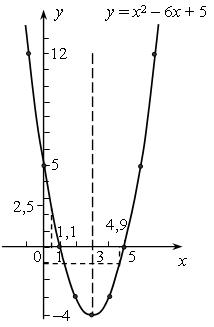
2. у = х2 – 6х + 5 – квадратичная функция, графиком является парабола.
Так как а > 0, то ветви направлены вверх. Найдем координаты (т; п) вершины параболы:
т = 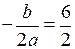 = 3; п = 9 – 18 + 5 = –4;
= 3; п = 9 – 18 + 5 = –4;
А (3; –4) – вершины параболы.
| х | –1 | |||
| у | –3 |
а) у ≈ 2,5;
б) х ≈ 1,1; 4,9;
в) у = 0 при х = 1 и х = 5;
г) у > 0 при х  (–∞; –1) (–∞; –1)  (5; +∞);
у < 0 при х (5; +∞);
у < 0 при х  (1; 5);
д) [3; +∞). (1; 5);
д) [3; +∞).
| 
|
3. а)  <
< 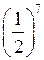 ; в) (–2,3)6 < (–4,1)6;
; в) (–2,3)6 < (–4,1)6;
б) (–1,7)3 < (0,4)3; г) 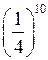 < (–1,4)10.
< (–1,4)10.
4. а)  ;
;
б) 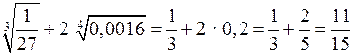 ;
;
в)  .
.
5.  ;
;
5а2 + 19а – 4 = 0;
D = 361 + 80 = 441;
а1, 2 =  ;
;
а1 =  , а2 = –4.
, а2 = –4.
6. х2 – 8х + 7.
1-й с п о с о б.
Выделим квадрат двучлена из квадратного трехчлена:
х2 – 8х + 7 = х2 –2 · 4 · х + 16 – 16 + 7 = (х – 4)2 – 9.
Это выражение принимает наименьшее значение при х = 4, и оно равно –9.
2-й с п о с о б.
у = х2 – 8х + 7 – квадратичная функция, графиком является парабола, ветви которой направлены вверх. Наименьшее значение квадратного трехчлена х2 – 8х + 7 – это ордината вершины этой параболы:
т =  = 4; п = 16 – 32 + 7 = –9;
= 4; п = 16 – 32 + 7 = –9;
–9 – наименьшее значение квадратного трехчлена х2 – 8х + 7.
– Конец работы –
Эта тема принадлежит разделу:
АЛГЕБРА 9 КЛАСС
Контрольная работа В а р и а н т а х х б у у Постройте график... Решение вариантов контрольной работы В а р и а...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: В а р и а н т 3
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов