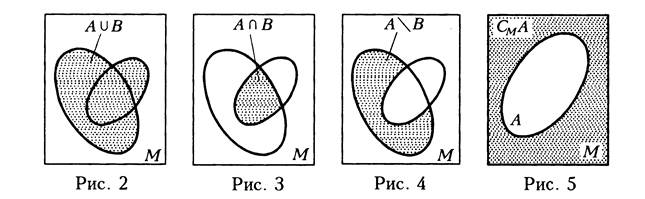
А. Множества и операции над ними. Действительные числа
А. Множества и операции над ними. Действительные числа.
Множества и действия над ними.
Множеством именуется некоторая совокупность элементов, объединенных по какому-либо признаку. Если есть такая совокупность, разумеется, как единое целое, говорят, что имеют дело с множеством. Приведенное определение не может рассматриваться как математически строгое, поскольку понятие множества является исходным, на основе него строятся остальные понятия математики. Тем не менее, из при веденного определения ясно, как можно говорить с множестве, например, действительных чисел или множестве плоских фигур. Если множество состоит из конечного числа элементов, оно называется конечным. Остальные множества называются бесконечными. Для множества используются следующие обозначения: А = {а,b,с,d}
Множество, в котором не содержится ни одного элемента, называется пустым. Обозначается оно знаком Ø.
Множества, состоящие из одних и тех же элементов, называют совпадающими. Например, совпадают два конечных множества, которые отличаются друг от друга порядком их элементов.
2. Отображения. Образ, прообраз, инъективность и сюръективность


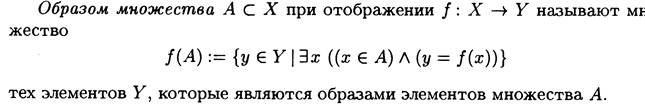

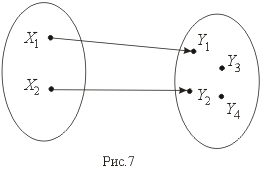
Отображение называется инъекцией, если для любых элементов x1, x2 Î X, для которых f(x1) = f(x2) следует, что x1 = x2. (рис. 7)
Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).

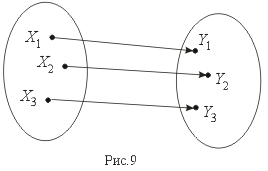
Биекция – это одновременно и сюръекция и инъекция (рис.9).
3. Мощность множества. Счетные множества и их свойства.


(определение счетного множества).Счетное
множество — это множество, эквивалентное множеству натуральных чисел.
Рассмотрим примеры счетных множеств.
Пример 11.
Множество всех целых чисел
Z = { 0, -1, 1, -2, 2, -3, 3,...,}.
Соответствие между целыми и натуральными числами можно осуществить по схеме
n « 2n+1 при n³ 0, n « 2|n| при n<0.
Множество всех четных положительных чисел. Соответствие по формуле n« 2n.
Множество чисел 2n. Соответствие осуществляется по формуле n « 2n.
Приведем некоторые свойства счетных множеств.