Гексагональных кристаллов

Гексагональная решетка, состоящая из трех решеток Бравэ, изображена на рис. 23. Ось направлена перпендикулярно плоскости рисунка.

Плоскости с первой по шестую (на рисунке изображены проекции граней на ось XOY) являются физически эквивалентными плоскостями, плоскости с 7 по 9 образуют другую совокупность физически эквивалентных плоскостей.

Обозначим все плоскости с помощью индексов Миллера:

1. ()

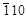2. (010)

3. (100)

4. ()

5. ()

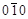6. ()

7. ()

8. (110)

9. ()

При таком способе обозначения трудно выделить, а тем более обозначить совокупность физически эквивалентных плоскостей.

Повернем систему координат вокруг оси Z на 120⁰ против часовой стрелки. При этом получим новую (штрихованную) систему координат, причем

, , .

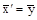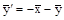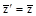– матрица перехода от старой к новой системе координат имеет вид

Рис. 23. Сечение гексагональной ячейки

.

Индексы плоскостей в новой системе координат (штрихованные) связаны с индексами в старой (нештрихованной) системе координат соотношением

.

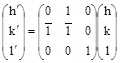«Займем» индекс из штрихованного набора и добавим четвертым индексом к нештрихованному набору . Этот индекс несвободный и не является четвертой координатой, он вводится для удобства обозначения.

.

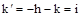
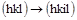Использование четырехиндексной системы позволяет структурно-идентичные плоскости проиндицировать при помощи формы , допускающей перестановку первых трех индексов.

Тогда те же плоскости в новой записи будут иметь вид:

1. ()®

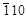2. (010)®

3. (100)®

4. ()®

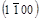
5. ()®

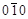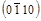
6. ()®

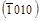
7. ()®

8. (110)®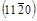

9. ()®

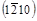
При вычислениях с помощью основных геометрических соотношений индекс «i» опускается. После вычисления снова вводится в конечный результат.

При обозначении направлений дополнительный индекс вводится следующим образом:

.

Так же, как и в случае обозначения плоскостей, при вычислениях четвертый индекс опускается.

При исследовании физических свойств кристаллов в различных направлениях используются образцы различной формы. Рассмотрим образец в виде прямоугольного параллелепипеда, вырезанный из полупроводникового материала, принадлежащего кубической системе. Необходимо определить все грани и ребра кристалла, если заданы некоторые параметры.

Рассмотрим конкретный пример (рис. 24).

Во-первых, из совокупности {110} необходимо выбрать плоскость, удовлетворяющую закону зон для данного случая, т. е. чтобы [112] лежало в этой плоскости.

, очевидно, что такой плоскостью может быть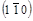

.

Рис. 24. Образец прямоугольного сечения

Это необходимо сделать еще и потому, что в геометрические соотношения подставляют индексы конкретных плоскостей и направлений.

Затем вспомним, что это кристалл кубической системы, следовательно, плоскость и нормаль к ней обозначаются одинаковым набором индексов. Следовательно, плоскость DАВС®(112), а направление СD®[].

Все параллельные прямые обозначаются одинаковым набором индексов Миллера, следовательно, все ребра горизонтальные имеют то же направление. Осталось определить верхнюю и нижнюю грань или ребра, параллельные направлению АD.

Определим индексы верхней грани. В этой плоскости одновременно лежат направления [112] и []. Составим систему уравнений и решим ее

.

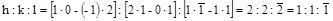Индексы искомой плоскости: .

Можно проверить, лежит ли в этой плоскости [112]:

.

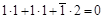Задача решена, определены все ребра и грани образца.

 

Стереографические проекции

Кристаллографические проекции

Для отображения внешнего вида кристалла в кристаллографии применяют аксонометрические и ортогональные проекции. Будучи наглядными, эти проекции не позволяют определять углы между различными ребрами и гранями кристалла.

В том случае, когда нас не интересуют размеры, удобно заменить реальный кристалл его точечным комплексом, образуемым при помощи параллельного переноса граней кристалла и его ребер до пересечения всех этих элементов в одной точке (центре тяжести), называемой центром комплекса.

При построении проекции элементы точечного комплекса отображаются на некоторую поверхность, называемую поверхностью проекций.

Рассмотрим различные типы проекций.

Сферическая проекция. Из центра точечного комплекса опишем сферу произвольного радиуса. Пересечение нормалей к граням кристалла с поверхностью сферы представляет собой сферическую проекцию нормалей к граням кристалла. Каждая нормаль (как и любое направление) проектируется на поверхность сферы проекцией в виде точки. Положение любой точки на поверхности сферы можно охарактеризовать двумя сферическими (полярными) координатами (рис. 25): r – полярное расстояние, отсчитываемое по любому направлению от 0⁰ (северный полюс) до 180⁰ (южный полюс); j – долгота, отсчитываемая по экватору от меридиана, принятого за нулевой.

Сферическая проекция кристалла наглядна, но для практического применения ее удобнее спроектировать на плоскость. Для этого пользуются стерео-, гномостереографическими и гномоническими проекциями.

Гномоническая проекция. Этот вид проекции широко применяют в рентгеноструктурном анализе. Плоскость гномонической проекции

Рис. 26. Стереографическая проекция направления

является касательной к северному полюсу сферы. Нормаль к грани кристалла, проведенная из центра сферы проекций, продолжается до пересечения с плоскостью проекции. Гномоническая проекция плоскости представляет собой точку, проекция направления – прямую. Координаты точек на гномонической проекции прямо пропорциональны индексам Миллера. Этот важный результат дает возможность определять символы граней непосредственно по гномонической проекции.

Стереографическая проекция. Принцип построения стереографической проекции показан на рис. 26.

За плоскость стереографической проекции выбирается экваториальная плоскость, на которую сфера проектируется в виде круга проекций. На сфере отмечается северный (N) и южный (S) полюсы. Для получения стереографической проекции прямой Оа₁ продолжаем эту прямую до пересечения со сферой. Точка А – есть сферическая проекция направления Оа₁. Соединим точку А с южным полюсом сферы S. Прямая АS пересекает плоскость проекции (экваториальную плоскость) в точке а. Эта точка есть стереографическая проекция направления Оа₁. Стереографические проекции направлений изображаются точками внутри круга проекций. Очевидно, что вертикальное направление проектируется как точка в центре круга проекций, горизонтальная – как две точки на экваторе.

Плоскость, проходящая через точку О и пересекающая сферу, – есть геометрическое место направлений, исходящих из точки О и лежащих в этой плоскости. Следовательно, стереографическая проекция плоскости есть геометрическое место стереографических проекций направлений, лежащих в этой плоскости, и соответственно этому плоскость, проходящая через точку О, проектируется на стереографическую проекцию в виде соответствующей дуги. Стереографические проекции горизонтальных плоскостей представляют собой окружности, совпадающие с границами круга проекций, проекции вертикальных плоскостей совпадают с диаметрами круга проекций, а проекции наклонных плоскостей изображаются дугами, опирающимися на концы диаметра круга проекций.

Важны следующие два свойства стереографических проекций:

1) любая окружность, проведенная на сфере, изображается на стереографической проекции также окружностью;

2) на стереографической проекции не искажаются пространственные угловые соотношения. Углы между дугами, проведенными на сфере проекции, сохраняются без искажений на плоскости проекций.

Стереографические проекции применяются для изображения элементов симметрии кристалла, при идентификации плоскостей и направлений, при структурном анализе.

Сетка Вульфа

Для решения количественных задач с помощью стереографической проекции пользуются градусными сетками. Наиболее употребительна сетка Вульфа. Сетка Вульфа – это, по существу, стереографическая проекция всей системы меридианов и параллелей, нанесенных на поверхность сферы. Плоскостью проекций является плоскость одного из меридианов. Положение любой точки на сетке Вульфа определяется ее сферическими координатами r и j (рис. 27). Сетка Вульфа стандартно чертится на круге диаметром 20 см, линии параллелей и меридианов проводятся через два градуса. Расстояние между ними можно на глаз разделить еще на четыре части, т. е. работать с точностью до 0,5 градуса.

 

Рис. 27. Сетка Вульфа