Геометрические уравнения

Геометрические уравнения выражают связь между деформациями стержней и такими перемещениями сечений стержней, которые не терпят разрывов в узлах и совместны с наложенными на систему связями.

В качестве примера рассмотрим простейшую стержневую систему, нагруженную силами в узле 2 (рис. 4,а), уравнения равновесия которого имеют вид

0,5N₁ = P,

0,866N₁ + N₂ = 2P.

Матрица уравнений равновесия узла: .

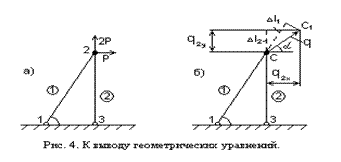Рассмотрим теперь произвольную деформацию системы, не связанную с конкретной нагрузкой, но не нарушающую целостности системы (рис. 4,б). Примем для определенности перемещение узла 2 из точки С в точку С₁, которое

характеризуется вектором 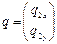. Величина и направление вектора q не связаны с действующими на систему силами.

Вычислим удлинения стержней, которые равны проекциям вектора q на осевые линии стержней:

D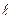₂ = q_2y, D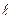₁ = q×cos(60⁰-a) = q×cosa×cos60⁰ + q×sina×sin60⁰ =

= q_2x×0,5 + q_2y×0,866.

Запишем эти уравнения в векторной форме:

или d = Cq.

Заметим, что матрица С совпадает с транспонированной матрицей А. Докажем, что совпадение носит не случайный характер и выражает статико-геометрическую аналогию в механике.

Пусть некоторая шарнирно-стержневая система находится в равновесии. Зададим узлам системы возможные перемещения, определяемые вектором dq. Возможная работа внешних узловых сил на перемещениях узлов равна dА^е = (dq)^Tp. Возможная работа внутренних усилий на деформациях, обусловленных вариацией узловых перемещений dq, равна

dAⁱ = - (dd)^T N = - (С dq)^TN = - (dq)^T C^T N.

Согласно принципу возможных перемещений для системы, находящейся в состоянии равновесия, справедливо равенство dА^е + dАⁱ = 0, или (dq)^T(p - C^TN) = 0. В силу произвольности вектора dq получаем p - C^TN = 0, или C^TN = p. Сравнивая полученное равенство с (1), заключаем, что A = C^T и С = А^Т.

Таким образом, векторное геометрическое уравнение связано с уравнением равновесия узлов через матрицу А и имеет вид:

d = A^Tq. (3)

В уравнении (3) оба вектора d и q являются неизвестными.

Итак, статико-геометрическая аналогия состоит в том, что по уравнению равновесия (1) может быть сформировано геометрическое уравнение (3) и, наоборот, из геометрического уравнения можно получить уравнение равновесия. Данная аналогия носит общий характер и проявляется не только в шарнирно-стержневых системах, но и в более сложных системах, если для них выполняется закон сохранения механической энергии.

По известным узловым перемещениям деформации элементов системы всегда определяются однозначно, так как, задаваясь вектором q, по уравнению (3) определяем вектор d. Обратная задача имеет решение не всегда.

Для статически определимой системы матрица А является квадратной. Геометрическая неизменяемость системы означает невырожденность этой матрицы. Тогда система (3) имеет единственное решение q = (A^T)^-1d, т.е. по деформациям элементов можно однозначно определить перемещения узлов.

Для статически неопределимой системы число скалярных уравнений в формуле (3) больше числа неизвестных, а размерность вектора d больше размерности вектора q. Для того, чтобы уравнение (3) могло быть разрешимо относительно вектора q, на вектор d должно накладываться определенное ограничение, называемое условием совместности деформаций. Запишем его в виде

Bd = 0. (4)

Выполнение этого условия гарантирует, что перемещения узлов могут быть определены по известным деформациям элементов.

Уравнение статики (1) и геометрическое уравнение (3) независимы друг от друга и не связаны с физическими параметрами системы. Следовательно, они пригодны для построения математических моделей систем с любыми физическими свойствами, например, для упругих или упругопластических систем.

Векторы p и q, N и d образуют пары так называемых двойственных переменных.