Дослідження структури звукових об’єктів

Структура звукового об’єкта і тембр.

Дослідження необхідне для розробки алгоритму розпізнавання музичних сигналів і для формування вимог до розроблюваної системи опрацювання сигналів. Крім того, треба дослідити зв’язок структури звукового об’єкту з відчуттями тембру. Для оцінки тембру звучання важливий не тільки момент його розпізнання, але і можливість зміни тембру в процесі виконання. Тут важливу роль відіграє динаміка зміни спектральної огинаючої в часі на всіх етапах звучання: атаки, стаціонарної частини, спаду.

Тому необхідно побудувати адекватну модель звукових об’єктів, придатних для синтезу і ідентифікації тембру.

Для цього необхідно:

1. Спостереження зміни параметрів гармонійних складових звукових об’єктів.

2. Виявлення загальних закономірностей в розгортанні гармонійних складових в різних музичних інструментів.

3. Вивчення впливу інтенсивності збудження і способу відтворення звуку на процес розвитку гармонійних складових.

4. Дослідження взаємодії гармонійних складових звукових об’єктів.

5. Встановити зв’язок гармонійної структури звукового об’єкта з тембром.

При аналізі сигналів треба опиратися на такі припущення:

1. Всі досліджувані сигнали відповідають одній ноті, а не співзвуччю.

2. Частоти натуральних призвуків основного тону (обертонів) приблизно кратні частоті основного тону.

3. Сигнал є квазіперіодичним: довжина повних циклів коливань має незначні відхилення від деякого середнього значення. На стадіях встановлення і затухання (атаки і спаду) ці відхилення не нормуються, а на стадії, яка встановилася відхилення періоду відповідає зміні висоти тону не більше четверті тону.

4. Середня тривалість повного циклу коливань є рівною тривалості одного циклу на стадії коливань, яка встановилася.

5. Сигнал можна розбити на ділянки приблизно однакової тривалості.

Дослідження кожного звукового об’єкта необхідно розбити на такі етапи:

1. Визначення орієнтовної тривалості повного циклу коливань Т;

2. Розбиття всього звукового об’єкта на не перекриваючі фрагменти, що відповідають окремим повним циклам коливань;

3. Для кожного циклу коливань виконуємо розклад в гармонійний ряд Фур’є на тривалості цього циклу.

4. Середнє значення амплітуд і початкових фаз обертонів в даному циклі коливань приймається рівним відповідно модулям і аргументам коефіцієнтів комплексної форми отриманого ряду Фур’є.

В результаті отримаємо набір амплітуд і фаз обертонів на кожному повному циклі коливань сигналу, знаючи при цьому точне значення тривалості кожного циклу.

Для дослідження вводиться поняття траєкторія амплітуди (фази) обертона – залежність середнього значення амплітуди (фази) в даному циклі коливань від номера циклу.

Обчисливши траєкторії амплітуд і фаз обертонів і виконавши їх графічне зображення можна приступити до їх аналізу.

1. Виявимо особливості траєкторій амплітуд і фаз обертонів для кожного інструмента в залежності від висоти тону і способу добування звуку.

2. Виявимо подібні риси траєкторій для кожного інструмента незалежно від висоти тону і способу добування і різницю в траєкторіях амплітуд і фаз обертонів різних інструментів.

3. Виявимо ступінь кореляції траєкторій амплітуд обертонів як випадкових функцій часу.

Дослідження проводились на ПЕОМ. Як звуковий матеріал взяті семпли – фрагменти звучання музичних інструментів. Для аналізу вони представлені у цифровому виді запису RIFF WAVE. Частота дискретизації фрагментів 44100 Гц., квантування – 16 бітне.

Програмне забезпечення повинно виконувати такі операції: читання файлів формату RIFF WAVE, визначення частоти основного тону,розклад в комплексний ряд Фур’є, формування траєкторій амплітуд і фаз обертонів, їх графічне відображення.

Визначення частоти основного тону сигналу:

1. Обчислюється короткочасна автокореляційна функція сигналу і визначається положення її максимуму t₀.

2. Виконується дискретне перетворення Фур’є на довжині 2t_0, обчислюється амплітудний спектр.

3. Визначається положення максимумів отриманого амплітудного спектру і знаходиться найменше загальне дільник F¢ частот, що відповідає цим максимумам.

4. За період сигналу приймається значення T=1/ F¢.

Далі проводиться розмітка сигналу (визначення часових меж кожного повного циклу коливань) одним з двох способів: за нулями чи за максимумами.

При розмітці за максимумами за тривалість даного циклу коливань сигналу умовно приймається віддаль між двома локальними (місцевими) максимумами сигналу, що відстають один від одного на віддаль T±t (T – довжина періоду основного тону). Для розмітки знаходиться найбільший локальний максимум сигналу - опорний (його положення за часом позначимо T_оп), положення наступного локального максимуму визначається пошуком в інтервалі (T_оп +T-Dt, T_оп +T+Dt) локального максимуму. Величину Dt встановлює користувач. Положення інших локальних максимумів знаходиться аналогічно: послідовно віддаляючись від найбільшого максимуму в обидві сторони. Графік розмітки за максимумами наведений рис 11, де Т¢ - довжину даного циклу коливань.

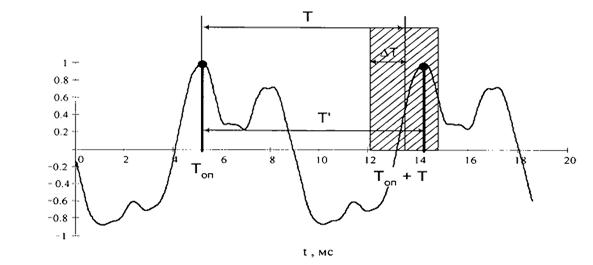
Рис. 11 Графік розмітки за максимумами

При розмітці за нулями за тривалість даного циклу коливань умовно приймається відстань між двома нульовими значеннями сигналу, що знаходяться на відстані Т±t. Для розмітки знаходиться найближче до найбільшого локального максимуму нульове значення (чи перехід через нуль) – опорне (його положення по часу позначимо Т_оп0). Положення наступного нульового значення (переходу через нуль) визначається пошуком в інтервалі (T_оп0 +T-Dt, T_оп0 +T+Dt) такого значення сигналу, для якого виконуються умови:

1. Значення сигналу точно чи приблизно рівне опорному значенню.

2. Співпадають знаки похідної сигналу в даній і в опорній точках.

Такий складний алгоритм вибраний тому, що сигнал не обов’язково прийме значення в інтервалі (T_оп +T-Dt, T_оп +T+Dt), оскільки форма сигналу змінюється від періоду до періоду через зміну співвідношень фаз і амплітуд обертонів. Крім того, можливо два і більше переходів через нуль в інтервалі (T_оп +T-Dt, T_оп +T+Dt), тоді ми повинні вибрати ту точку, в якій співпадає знак похідної з знаком похідної в опорній точці. Графік розмітки за нулями наведений рис 12.

Алгоритм ілюструється на рис. 12

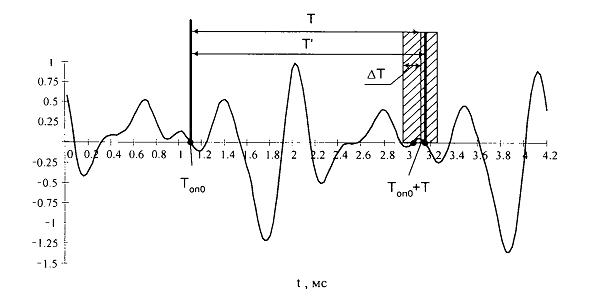
Рис.12 Графік розмітки за нулями

Після розмітки сигналу відомі часові межі кожного повного циклу коливань (тривалість кожного циклу), тобто вже можна скласти траєкторію тривалості циклу коливань сигналу.

Позиції (номери) граничних відліків кожного періоду зберігаються в пам’яті, користуючись ними, можна зчитати з вхідного файлу масив відліків, який відповідає одному повному циклу і виконати дискретне перетворення Фур’є на тривалості даного циклу. Операції з ваговими функціями не виконуються, оскільки кожен період обмежений з обох сторін майже рівними значеннями. За коефіцієнтами розкладу визначаються значення амплітуд і фаз обертонів в даному циклі коливань. Усереднені по всім повним циклам значення амплітуд і фаз обертонів складають усереднений спектр звукового об’єкту.

Для оцінки статичної залежності траєкторій амплітуд обертонів як функцій часу обчислюється матриця коефіцієнтів кореляції сукупності випадкових величин, що складені з траєкторій амплітуд обертонів. Елемент матриці R_ij дорівнює коефіцієнту кореляції траєкторій амплітуд і-го та j-го обертонів. Коефіцієнт кореляції R_ij обчислюється згідно з виразом (3)

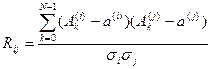, де (3)

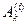- значення траєкторії амплітуди і-го обертону на k-му циклі коливань;

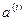- середнє значення траєкторії амплітуди і-го обертону;

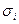- дисперсія траєкторії амплітуди і-го обертону;

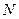- кількість повних циклів коливань на протязі тривалості даного звукового об’єкту.

Одною з характеристик звукового об’єкту є матриця коефіцієнтів кореляції траєкторії амплітуд обертонів. Значення коефіцієнтів кореляції траєкторій амплітуд для різних інструментів наведені на рис.13. і рис.14.

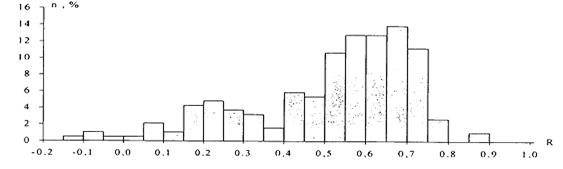
Рис.13. Гістограми коефіцієнта кореляції траєкторій амплітуд обертонів для інструментів з автоколиваннями

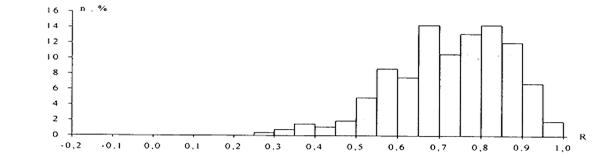
Рис.14. Гістограми коефіцієнта кореляції траєкторій амплітуд обертонів для інструментів з вільними коливаннями

За значеннями коефіцієнтів кореляції (гітари і фортепіано – 0-0,8; для дерев’яних духових – 0,5-0,9; для мідних – 0,75- 0,99) можна зробити висновок, що вільним коливанням властивий слабкий взаємозв’язок окремих гармонійних складових, для стабільних автоколивань властива майже функціональна залежність між амплітудами обертонів (коефіцієнт кореляції 0.99).

Для аналізу звукового об’єкту необхідно знати: усереднений амплітудний спектр коливань, траєкторії амплітуд обертонів, перехідні процеси (атака), негармонійні призвуки.