Виды погрешностей и методы их расчета

 

Точность размеров поверхностей изделий, их формы, взаимного расположения, обеспечиваемая различными технологическими метода­ми, служит основой для проектирования технологических процессов механической обработки. В этой связи анализ погрешностей (как меры точности), их расчет и классификация являются важнейшими вопросами технологии машиностроения. Точность изделия является важнейшей характеристикой его качества, так как повышение точности способствует повышению долговечности изделия, повышает надежность и конкурентоспособность.

При изготовлении заготовок, при механической обработке, контроле, сборке возникают различного рода погрешности, как отклонения параметров от требуемых.

В зависимости от причин их вызывающих погрешности можно разделить на следующие виды: систематические (постоянные и изменяемые закономерно) и случайные.

Систематические постоянные погрешности не изменяются при обработке заготовок в одной партии. Они возникают под воздействием постоянно действующих факторов (погрешности оборудования, оснастки, управляющих программ станков с ЧПУ).

Систематические закономерно изменяющиеся (функциональные) погрешности могут быть непрерывные и периодически повторяющиеся.

Случайные погрешности возникают в результате действия большого числа факторов не связанных между собой, их величину заранее определить невозможно.

Расчет погрешностей может осуществиться одним из методов:

Расчетно-аналитический метод применяется при изготовлении уникальных и точных изделий в условиях единичного и серийного производства. При этом расчеты сопровождаются применением эмпирических и аналитических формул.

Вероятностно-статистический – применяется при изготовлении большой партии и позволяет без раскрытия сущности процессов или явлений произвести оценки погрешностей (первичных и суммарных).

Расчетно-статистический, при котором часть первичных погрешностей определяется расчетно-аналитическим методом, а часть статистическим методом.

При различных методах механической обработки получаемые рассеяния размеров подчиняются некоторым математическим законам: нормального распределения (закон Гаусса), равной вероятности, равнобедренного треугольника (закон Симпсона), эксцентриситета (закон Релея) и др.

Закону Гаусса подчиняются погрешности деталей, полученные при обработке на настроенных станках, при квалитетах точности IT8 и грубее. Применение этого закона связано с тем, что суммарная погрешность формируется при одновременном воздействии многих первичных погрешностей, зависящих от станка, инструмента, приспособления, состояния заготовки (метода ее получения) и т.п. Уравнение кривой нормального распределения имеет вид:

 

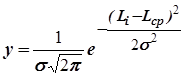, (16)

 

где s - среднее квадратичное отклонение:

 

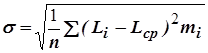. (17)

 

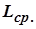- среднее арифметическое значение действительных размеров заготовки данной партии:

 

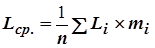, (18)

 

где 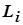– действительный размер;

m_i – число заготовок данного интервала размеров (частота);

n – число заготовок в партии;

е – основание натурального логарифма.

В качестве приближенной меры точности может служить поле рассеяния размеров ω, которое можно принять по полигону измерений (L_max-L_min). Кривая нормального распределения имеет симметричный характер с максимальным значением ординаты в точке соответствую­щей среднему арифметическому значению действи­тельного размера (рис. 9 а).

В точках, удаленных на ±3s, кривая асимптотически приближается к оси абсцисс. На практике принято, что площадь, заключенная между кривой и осью абсцисс и ограниченная полем рассеяния ω= 6s, приблизительно равна 1 (погрешностью 0,27%). Чем меньше s, тем меньше поле рассеяния и кривая вытянута вверх (рис. 9 б).

 

а) б)

 

Рис. 9. Кривые нормального распределения

 

Расчет вероятности получения годной детали и брака при механической обработке, в случае, когда рассеяние действительных размеров подчиняется закону нормального распределения, произво­дится следующим образом (рис.10):

 

 

 

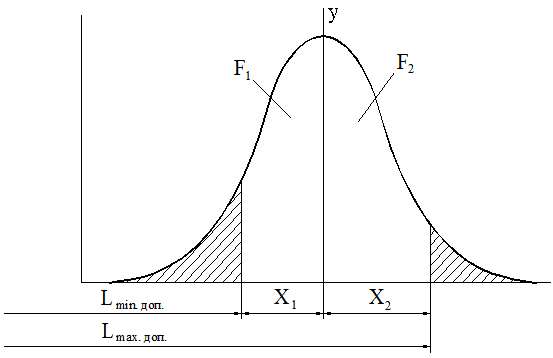
Рис.10. К расчету вероятности получения годных деталей и брака

 

Если поле рассеяния определяется допуском Т (размерами Х₁ и Х₂ от центра группирования), то вероятность получения годных деталей будет определятся отношением суммы площадей F₁ + F₂ к площади, заключенной кривой:

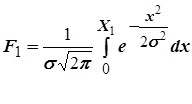, (19)

 

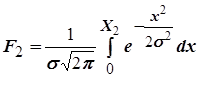. (20)

Эти интегралы удобно представить в виде нормированной функции Лапласа:

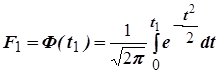, (21)

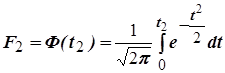. (22)

 

Вероятность получения годной детали определяется суммой площадей W=F₁+F₂, а брака – Q=1 – W.