Лекция № 12. НЕОРИЕНТИРОВАННЫЕ ГРАФЫ
Лекция № 12. НЕОРИЕНТИРОВАННЫЕ ГРАФЫ
Основные определения
Каждое ребро e из E инцидентно ровно двум вершинам и , которые оно соединяет. При этом вершина и ребро e называются инцидентными друг другу, а… Принято обозначение n для числа вершин графа (мощность множества ): и m для… Если все ребра графа неориентированные, т.е. пары вершин, определяющие элементы множества E, неупорядочены, то такой…Радиус, диаметр и центр графа
Эксцентриситет вершины графа – расстояние до максимально удаленной от нее вершины. Для графа, для которого не определен вес его ребер, расстояние… Радиус графа – минимальный эксцентриситет вершин, а диаметр графа –… Центр графа образуют вершины, у которых эксцентриситет равен радиусу. Центр графа может состоять из одной, нескольких…Эйлерова цепь
Рис. 12.4. Схема Кенигсбергских мостовРеберный граф
Английское название реберного графа – line graph, отсюда и обозначение графа – L(G). На рис. 12.7 показан реберный граф (он выделен жирными… Рис. 12.7. Реберный графРаскраска графа, хроматический полином
Упростим задачу. Будем использовать меньшее количество красок, но при этом не будем допускать, чтобы соседние страны, имеющие общие границы, были… Ответить на этот вопрос можно с помощью теории графов. Для этого нужно… Произвольная функция на множестве вершин графа называется раскраской графа. Раскраска называется правильной, если для…Ранг-полином графа
Ранг-полином графа G имеет вид , где – ранг графа G , а – коранг остовного (т.е. включающего в себя все вершины графа) подграфа H, а – его ранг.…Циклы
Маршрут, в котором начало и конец совпадают, – циклический. Циклический маршрут называется циклом, если он – цепь.
Остовом графа G называется граф, не содержащий циклов и состоящий из ребер графа G и всех его вершин. Остов графа определяется неоднозначно.
Ребра графа, не входящие в остов, называются хордами. Цикл, получающийся при добавлении к остову графа его хорды, называется фундаментальным относительно этой хорды.
Теорема 12.11. Число ребер неографа, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно цикломатическому рангу графа.
Пример 12.8. По заданной матрице смежности:
,
определить число циклов длины 3 (
) и длины 4 (
). Записать матрицу фундаментальных циклов.
Решение. Матрица смежности данного графа симметричная, поэтому ей соответствует неориентированный граф. Сумма ненулевых элементов матрицы равна 12, следовательно, по лемме о рукопожатиях в графе 6 ребер. Построим этот граф (рис. 12.10). Очевидно, в нем два цикла (3–4–5 и 1–3–5) длиной 3 и один цикл (1–3–4–5) длиной 4. В данной задаче решение получено прямым подсчетом по изображению графа. Для более сложных случаев существует алгоритм решения задачи по матрице смежности.
Известно, что след (trace) матрицы смежности, возведенный в k-ю степень, равен числу циклических маршрутов длины k (см. теорему 12.4). Это число включает в себя и искомое число циклов. Цикл отличается от циклического маршрута тем, что в нем не повторяются ребра. Кроме того, предполагается, что искомые циклы не помечены, а в след матрицы входят именно помеченные маршруты.
Рис. 12.10
Непомеченных циклов длиной 3 в 6 раз меньше, чем помеченных, так как каждый помеченный цикл может отличаться началом (а их в данном случае три) и двумя направлениями обхода (по и против часовой стрелки). Возведем заданную матрицу смежности в третью степень:
,
и получим
.
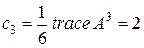Поскольку циклических маршрутов длиной 3, отличных от циклов длиной 3, не существует, найденное число и есть ответ в поставленной задаче.
С циклами длиной 4 немного сложнее. В след четвертой степени матрицы смежности графа
,
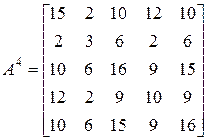входят не только циклы, но и циклические маршруты с двойным и четырехкратным прохождением ребер. Обозначим количество таких маршрутов через 
и 
соответственно. Очевидно, число маршрутов с четырехкратным прохождением одного ребра для вершины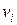 
равно степени этой вершины: 
. Число маршрутов с двукратным прохождением ребра складывается из числа 
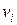с висячей вершиной и числа 
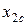маршрутов с вершиной 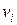в центре.
Легко заметить, что 
. Число зависит от степеней вершин, соседних с :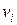
,
где 
– ребро, инцидентное вершинам i и k.
Для графа на рис. 12.10 получим
,
,
,
.
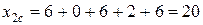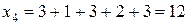С учетом того, что непомеченных циклов длиной 4 в 8 раз меньше, получим
.
После преобразований формула примет вид
.
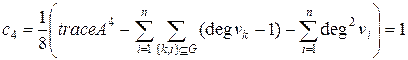Для нахождения матрицы фундаментальных циклов пронумеруем ребра графа, начиная нумерацию с хорд, как показано на рис. 12.11 (а).
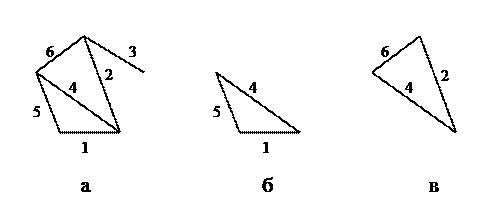
Рис. 12.11
Двум хордам, 1 и 2, соответствуют два фундаментальных цикла: 1–4–5 и 2–4–6 (рис. 12.11 (б и в)). Матрица фундаментальных циклов имеет две строки (число циклов) и шесть столбцов (число ребер).
В первой строке матрицы единицами отмечены столбцы с номерами ребер, входящих в первый цикл, а во второй строке – номера ребер из второго цикла.
Лекция № 13. ОРИЕНТИРОВАННЫЕ ГРАФЫ
Основные определения
Многие понятия, введенные для неографов, для орграфов приобретают другое определение. Матрица расстояний для орграфа несимметрична, и эксцентриситет… Основание орграфа – неограф с теми же вершинами, но ребрами вместо… Маршрут в орграфе – последовательность вершин, соединенных дугами, направленными в одну сторону.Маршруты в орграфе
Пример 13.1. Дан орграф (рис. 13.1). Сколько в нем маршрутов длиной 3? Рис. 13.1Транзитивное замыкание
Отношение на X рефлексивно, если для любого пара . Отношение на X антирефлексивно, если для любого пара . Отношение на X симметрично, если для любой пары из условия следует .Компоненты сильной связности графа
Основание орграфа – неограф с теми же вершинами, но ребрами вместо соответствующих дуг. Орграф называется связным, если связно его основание. Вершина u достижима из вершины v, если существует маршрут из v в u.Лекция № 14. ДЕРЕВЬЯ