рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Реферат Курсовая Конспект
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ - раздел Философия, Лекция 8. ПОНЯТИЕ ФУНКЦИИ Разделяй И Властвуй. (Главное, Нужно Знать, Что Разделять, Чтобы П...
Разделяй и властвуй.
(Главное, нужно знать, что разделять,
чтобы потом властвовать.)
ПЛАН
1. Введение
2. Историческая справка.
3. Приращение аргумента и функции.
4. Задачи, приводящие к понятию производной.
5. Производная функции, заданной аналитически.
6. Таблица производных.
7. Связь между непрерывностью и дифференцируемостью.
8. Геометрический смысл производной. Графическое дифференцирование.
9. Производная функции, заданной таблично.
10. Дифференциал функции. Приложение к приближенным вычислениям.
11. Экономический смысл производной.
12. Эластичность.
13. Заключение
11.1. Введение
– Слушай, а почему исчисление? Вычисление – то лучше.
– Не лучше. Приставки «из» и «ис» означают высшую степень какого-то действия: из-вержение, из-неможение, ис-коренение.
– Из-вращение, ис-кушение! Значит ис-числение
– Высшая степень вычислений.
(Из разговора студентов).
11.2. Историческая справка
Создание дифференциального и интегрального исчислений относится к концу 17 – началу 18 веков, когда на смену мрачного Средневековья пришла Эпоха Просвещения. Церковь потихоньку сдавала свои позиции, костры все реже загорались на тесных площадях европейский городов и Наука радостно раскрывала свои тайны всем, кто мог ею заниматься всерьез. Европа и Англия, Лейбниц и Ньютон, бедняк и богач стояли у истоков реки новых математических знаний. Вслед за удивительным Декартом они искали универсальный язык формул, которым можно было описать мироздание, где все текло и все менялось. Как описать изменение? И не просто изменение, а изменение одной величины под воздействием изменения другой? У них был разный путь. Если вспомнить способы задания функции: аналитический, табличный, графический.
| формула | таблица | график | ||||||||||
|
| 
| ||||||||||

| 
| 
|
то подход Ньютона был аналитически-кинематическим. Он мыслил категориями физики – скоростями или быстростями и часто в роли независимой переменной у него выступало время 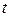 .
.
Лейбниц ушел от привязки к конкретным физическим величинам. Он был геометр – его характеристический треугольник со сторонами 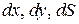 присутствует во многих работах. Скорость изменения переменной
присутствует во многих работах. Скорость изменения переменной  , связанной с изменением переменной
, связанной с изменением переменной 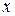 он впервые записал в виде
он впервые записал в виде  , если
, если 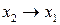 и
и 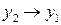 .
.
Но им нужна была не скорость, а мгновенная скорость, не просто приращения, а отношение бесконечно малых приращений. Наверное, они оба хотели остановит и зафиксировать мгновение. Понятие предела появилось позже, но они интуитивно чувствовали, когда бесконечно- малую величину можно считать равной нулю, а когда нельзя.
Их подход к исследованию функций остался актуальным и сейчас, потому что как и прежде человечеству необходимо знания и мгновения, и вечности.
Основополагающими терминами дифференциального исчисления являются понятия приращение – производная - дифференциал. Рассмотрим их при аналитическом, графическом и табличном способе задания функции.
11.3. Приращение аргумента и функции
Пусть дана функция и два значения ее аргумента 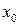 и x. Им соответствует два значения функции
и x. Им соответствует два значения функции  и
и 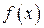 .
.
Определение 11.1. Разность значений
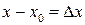 (11.1)
(11.1)
называется приращением аргумента в точке 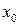 .
.
Определение 11.2. Разность значений функции
 (11.2)
(11.2)
называется приращением функции в точке 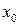 .
.
Разрешим равенства (11.1) и (11.2), данные в определении относительно 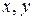 ,
,  и
и 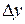 :
:
 . (11.3)
. (11.3)
С учетом (11.3) запишем приращение 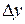 в виде:
в виде:
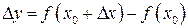 . (11.4)
. (11.4)
Здесь 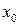 и
и  являются фиксированными постоянными значениями, а
являются фиксированными постоянными значениями, а 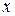 и
и 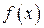 – переменными, зависящими от
– переменными, зависящими от  . Приращение
. Приращение  может быть различным – положительным, отрицательным или равным нулю.
может быть различным – положительным, отрицательным или равным нулю.
Покажем, как различные приращения аргумента  приводят к различным приращениям
приводят к различным приращениям 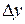 на примере.
на примере.
Пример 11.1. Найти приращение 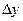 , связанное с приращением
, связанное с приращением 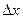 для функции
для функции  в общем виде и при переходе из точки
в общем виде и при переходе из точки 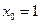 в точку
в точку 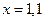 .
.
Решение. По формуле (11.4) найдем 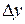 :
:
1.  . (11.5)
. (11.5)
2. По формуле (11.2) найдем приращение функции при
а)  .
.
б) с другой стороны подставим 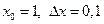 в формулу (11.5)
в формулу (11.5)

Получили равные результаты.
Если аргументу дать отрицательное приращение  , то приращение функции
, то приращение функции 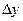 будет равно
будет равно  , т. е. равные по модулю приращения
, т. е. равные по модулю приращения 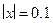 приводят к неравным по модулю приращениям функции
приводят к неравным по модулю приращениям функции  . Это связано с нелинейностью функции.
. Это связано с нелинейностью функции.
Если функция задана графически, то ее приращения 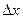 и
и 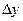 находят из графика (рис. 11.1).
находят из графика (рис. 11.1).

– Конец работы –
Эта тема принадлежит разделу:
Лекция 8. ПОНЯТИЕ ФУНКЦИИ
ПОНЯТИЕ ФУНКЦИИ... Все течет и все меняется Гераклит... Таблица Х х х х Y у у у у у...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?


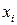



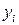

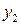






Новости и инфо для студентов