Метод подвижного базиса и уравнения Френе

 

Одной из задач теоретической механики является изучение траекторий движения материальной точки. Поскольку траектория есть линия в трехмерном пространстве, то эта задача решается средствами дифференциальной геометрии. Удобный метод анализа любой линии связан с так называемым подвижным базисом и уравнениями Френе. В каждой точке заданной кривой вводится ортонормированный базис , направление векторов которого при перемещении точки вдоль кривой изменяется в соответствии с ее формой.

Пусть кривая задана параметрическими уравнениями

 

(5.1)

 

где - радиус-вектор точек кривой, а 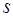- длина ее дуги. Следовательно

 

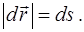(5.2)

 

Введем обозначение

(5.3)

 

 

Вектор - единичный касательный к кривой в

 

 

-22-

без ограничения общности примем 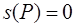. Тогда используя уравнения (5.12 b, c, d) Френе, получаем

 

Введем декартовы координаты в направлениях векторов и 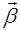соответственно, начало которых совместим с точкой на кривой (см. рис. 2).

 

 

 

 

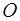
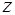
Рис.2.

-27-

. (5.13a-d)

 

Три уравнения Френе (5.12 b, c, d) составляют замкнутую систему дифференциальных уравнений для трех векторных функций подвижного базиса. Они единственным образом определяют форму кривой в трехмерном пространстве, если известны две функци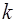и и 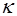длины дуги 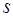кривой. Положение же этой кривой в пространстве регулируется уравнением (5.12a). Его решение 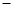единственно, если заданы точка , через которую проходит кривая, и ее направление в точке . Функция называется кривизной, соответственно 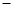радиусом кривизны, а функция называется кручением кривой. 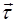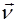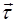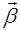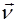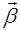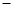Плоскость, которой принадлежат векторы и , принято называть соприкасающейся плоскостью; плоскость, в которой лежат векторы и , спрямляющей; а плоскость с векторами и соответственно нормальной. Векторы 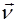и 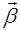называются соответственно нормалью и бинормалью к кривой, поскольку оба они ортогональны к касательному к кривой вектору .

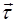Выясним геометрический смысл функций и . Для этого разложим векторную функцию 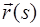в ряд Тейлора в окрестности произвольной точки кривой. За начальную точку отсчета длины дуги

может быть принята любая точка на кривой, поэтому

-26-

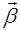
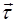каждой ее точке

(5.4)

Дифференцируя это

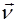равенство по 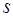, получаем

(5.5)

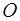Векторы 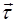и

Рис.1 ортогональны друг к другу. Обозначим модуль вектора через , а единичный вектор в направлении , соответственно, через 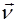. Теперь вектор можно представить в следующем виде:

 

(5.6)

 

И, наконец, определим вектор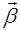такой, что

(5.7)

Из определений (5.3), (5.7) и равенств (5.4) 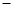(5.6) следует, что

 

-23-

(5.8)

 

Три единичных ортогональных друг к другу вектора и 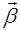(см. рис.1) в каждой точке заданной кривой образуют подвижный ортонормированный базис Его часто называют еще естественным базисом кривой, как и длину дуги 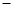естественным параметром кривой. Векторы подвижного базиса удовлетворяют трем уравнениям Френе. Одно из них совпадает с (5.6a). Для получения остальных двух уравнений продифференцируем векторную функцию , и полученный вектор разложим по векторам подвижного базиса

 

(5.9)

 

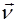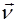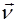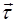здесь - коэффициенты разложения. Из единичности вектора следует, что вектор ортогонален вектору поэтому . Сложив равенства (5.6a) и (5.9), предварительно умножив их скалярно на и соответственно, и учтя ортогональность векторов 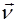и 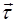, получим . Обозначив оставшийся не определенным коэффициент через 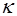, перепишем равенство (5.9) в виде

 

-24-

 

(5.10)

 

Продифференцируем теперь равенство (5.7), определяющее вектор 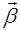, и воспользуемся уравнениями (5.6 a) и (5.10). Получим уравнение

 

(5.11)

 

Уравнения (5.10) и (5.11) и есть недостающие два из трех уравнений Френе, которые описывают изменение пространственной ориентации естественного базиса кривой при перемещении вдоль нее. Сведем их вместе с определением (5.3) касательного к кривой единичного вектора 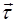в единую систему дифференциальных уравнений в обыкновенных производных:

(5.12a)

 

(5.12b)

(5.12c)

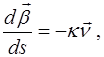(5.12d)

 

-25-