Инвестиции в В

$5000

-$2000 $1500

$500 $5000

-$2000 $1500

$500

Для оценки различных альтернатив, показанных на рис. 14.5, необходимо вычис­лить апостериорные вероятности P{hi,| v), указанные на соответствующих ветвях,

Глава 14. Теория игр и принятия решений

выходящих из узлов 4-7. Эти апостериорные вероятности вычисляются с учетом дополнительной информации, содержащейся в рекомендациях друга, с помощью следующих действий.

Шаг 1. Условные вероятности P{i>.| т} для данной задачи запишем сле­дующим образом.

0,9	0,1
0,5	0,5

Шаг 2. Вычисляем вероятности совместного появления событий.

P{m_t, v} = P{vj т}Р{т^ для всех / и j.

При заданных априорных вероятностях Р{ш,} = 0,6 и Р{т₂) = 0,4 ве­роятности совместного появления событий определяются умноже­нием первой и второй строк таблицы, полученной на шаге 1, на 0,6 и 0,4 соответственно. В результате имеем следующее.

V2

mi

0,54	0,06
0,20	0,20

Сумма всех элементов этой таблицы равна 1. Шаг 3. Вычисляем абсолютные вероятности.

p{v_;}= X P{^mi'^vj} ^для всех/

но всем /'

Эти вероятности получаются путем суммирования элементов соот­ветствующих столбцов таблицы, полученной на шаге 2. В итоге имеем следующее.

	P{v2)
0,74	0,26

Шаг 4. Определяем искомые апостериорные вероятности по формуле

Эти вероятности вычисляются в результате деления каждого столбца таблицы, полученной на шаге 2, на элемент соответствующего столб­ца таблицы, вычисленной на шаге 3, что приводит к следующим ре­зультатам (округленным до трех десятичных знаков).

V1 v₂

0,730	0,231
0,270	0,769

14.2. Принятие решений в условиях риска

Это те вероятности, которые показаны на рис. 14.5. Они отличаются от исходных априорных вероятностей Р{т^ = 0,6 и Р{т₂} = 0,4.

Теперь можно оценить альтернативные решения, основанные на ожидаемых пла­тежах для узлов 4-7.

Мнение "за"

Доход от акций компании А в узле 4 = 5000 х 0,730 + (-2000) х 0,270 = 3110 (долл.). Доход от акций компании В в узле 5 = 1500 х 0,730 + 500 х 0,270 = 1230 (долл.). Решение. Инвестировать в акции компании А. Мнение"против"

Доход от акций компанииАв узле 6 = 5000 х 0,231 + (-2000) х 0,769 = -383 (долл.). Доход от акций компании В в узле 7 = 1500 х 0,231 + 500 х 0,769 = 731 (долл.). Решение. Инвестировать в акции компании В.

Заметим, что предыдущие решения эквивалентны утверждению, что ожидаемые платы в узлах 2 и 3 равны 3110 и 731 долл. соответственно (рис. 14.5). Следова­тельно, при известных вероятностях i³{v₁} = 0,74 и P{v₂} = 0,26, вычисленных на шаге 3, можно определить ожидаемую плату для всего дерева решений (упражнение 14.2.2.3).

Вычисление в Excel апостериорных вероятностей. Шаблон Excel chl4Bayes-Posterior.xls вычисляет апостериорные вероятности для заданных матриц условных вероятностей, которые не должны превышать размер 10x10. Для вычислений необ­ходимо задать вероятности Р{т} и P{v т}. Excel проверит входные данные на нали­чие ошибок и при их обнаружении выведет соответствующее сообщение. На рис. 14.6 показано применение шаблона для решения задачи примера 14.2.2.

1 А	В I С | 0 I E I L	M l-N'j
	Bayes Posterior Probabilities
	Input Data	Output Results
з		|P{v|m) (10x10) maximum	P{v,m}
	P	[m> j v1 v2	v1 v2
	ml	0.6! 0.9 0.1	0 5400 0 0600
	m2	0.4J 0.5 0.5	0.2000 0 2000
	Input Data Error Messages	P{v}
			0.7400 0.2600
"17			P{m|v}
1S			0.7297 0.2308
		m2	0.2703 0.7692

Рис. 14.6. Вычисление в Excel апостериорных ве­роятностей для примера 14.2.2

УПРАЖНЕНИЯ 14.2.2

1. Несмотря на сезон дождей, Джим Боб планирует завтра идти на рыбалку, но только если не будет дождя. Из данных о погоде прошлых лет следует, что имеет­ся 70% -ная вероятность, что в сезон дождей будет идти дождь. В шесть часов ве­чера синоптики предсказали с 85% -ной вероятностью, что завтра будет дождь. Следует ли Джиму Бобу планировать рыбалку на завтра?

Глава 14. Теория игр и принятия решений

2. Фирма "Электра" получает 75 % электронных деталей от поставщика А и 25 % — поставщика В. Доля брака в продукции поставщиков А и В составля­ет 1 и 2 % соответственно. При проверке пяти деталей из полученной партии обнаружена лишь одна дефектная. Определите вероятность того, что партия получена от поставщика А. Проведите аналогичные вычисления относительно поставщика В. (Подсказка. Вероятность появления бракованной детали в пар­тии подчиняется биномиальному закону распределения.)

3. Предположим, что в задаче из примера 14.2.2 есть дополнительный выбор, связанный с инвестированием 10 ООО долл. в надежный депозит, который приносит 8 % прибыли. Совет вашего друга по-прежнему относится к инве­стированию через биржу.

a) Постройте соответствующее дерево решений.

b) Какое оптимальное решение в этом случае? (Совет. Используйте вероят­ности P{v_y) и P{v₂), полученные на шаге 3 в примере 14.2.2, для вычисле­ния ожидаемой суммы инвестирования через биржу.)

4. Допустим, вы являетесь автором романа, который обещает быть популяр­ным. Вы можете либо самостоятельно напечатать роман, либо сдать его в из­дательство. Издательство предлагает вам 20 ООО долл. за подписание кон­тракта. Если роман будет пользоваться спросом, будет продано 200 000 экземпляров, в противном случае — лишь 10 000 экземпляров. Издательство выплачивает авторский гонорар в сумме один доллар за экземпляр. Исследо­вание рынка, проведенное издательством, свидетельствует о том, что сущест­вует 70%-ная вероятность, что роман будет популярным. Если же вы сами напечатаете роман, то понесете потери в сумме 90 000 долл., связанные с пе­чатанием и маркетингом, но в этом случае каждый проданный экземпляр принесет вам прибыль в два доллара.

a) Принимая во внимание имеющуюся информацию, вы примете предложе­ние издательства или будете печатать роман самостоятельно?

b) Предположим, что вы заключили договор с литературным агентом на ис­следование, связанное с потенциальным успехом романа. Исходя из преды­дущего опыта, компания извещает вас, что если роман будет пользоваться спросом, то исследование предскажет неверный результат в 20 % случаев. Если же роман не станет популярным, то исследование предскажет верный результат в 85 % случаев. Как эта информация повлияет на ваше решение?

5. Вернитесь к проблеме выбора решения фермером Мак-Коем из упражне­ния 14.2.1.2. Фермер имеет дополнительный выбор, связанный с использо­ванием земли как пастбища, что гарантированно принесет ему прибыль в 7500 долл. Фермер получил также дополнительную информацию от броке­ра, касающуюся степени стабильности будущих цен на продукцию. Оценки брокера "благоприятный — неблагоприятный" выражаются количественно в виде следующих условных вероятностей.

ai а₂

0,15	0,85
0,50	0,50
0,85	0,15

14.2. Принятие решений в условиях риска

В данном случае а, и а₂ — оценки брокера "благоприятный" и "небла­гоприятный", a s,, s₂ и s₃ представляют изменение в будущих ценах: соответ­ственно "понижение", "такие же", "повышение".

a) Постройте соответствующее дерево решений.

b) Найдите оптимальное решение задачи.

6. Пусть в упражнении 14.2.1.5 дирекция компании решила провести пробную продажу своей продукции в выбранных населенных пунктах. Результатом пробной продажи являются оценки "хорошо" (а,) или "плохо" (а₂). Тест дает следующие условные вероятности с проведением рекламной кампании и без нее.

Р{ау| vft с рекламной кампанией Р{а_у| vij без рекламной кампании

V1	0,95	0,05	И/1	0,8	0,2
V2	0,3	0,7	W2	0,4	0,6

Здесь v_x и v₂ обозначают соответственно "успех" и "неуспех", a w_x и w₂ — "восприимчивый" и "невосприимчивый" покупатель.

a) Постройте соответствующее дерево решений.

b) Определите оптимальный план действий фирмы.

7. Статистические данные о работе компании показывают, что с вероятностью 5 % произведенная партия продукции будет неприемлемой (плохой). Плохая партия содержит 15 % дефектных изделий, а хорошая — лишь 4 %. Пусть значение переменной а = а, (= а₂) обозначает, что партия изделий является хорошей (плохой). Тогда соответствующие априорные вероятности равны со­ответственно Р{а = а,} = 0,95 и Р{а = а₂} = 0,05.

Вместо того чтобы отправить партии продукции с характеристиками, осно­ванными на априорных вероятностях, из каждой партии проверяются два изделия. Возможны следующие результаты проверки.

Оба изделия являются качественными (s,).

Одно изделие является качественным (s₂).

Оба изделия являются бракованными (s₃).

a) Определите апостериорные вероятности P{a_t s}, i = 1, 2; j = 1, 2, 3.

b) Предположим, что фирма отправляет партии продукции двум потребите­лям А и В. Контракты с ними определяют, что процент бракованных из­делий в поставках не должен превышать 5 и 8 % соответственно. Преду­сматривается штраф в 100 долл. за превышение на один процент максимально допустимого лимита бракованных изделий. Поставка пар­тий лучшего качества, чем указано в контракте, приносит производителю прибыль в 80 долл. за каждый процент уменьшения доли бракованных изделий. Постройте соответствующее дерево решений и определите при­оритетную стратегию отправки партий продукции.

Функции полезности. В предыдущих примерах критерий ожидаемого значения применялся лишь в тех ситуациях, где платежи выражались в виде реальных де­нег. Зачастую возникают ситуации, когда при анализе следует использовать скорее

Глава 14. Теория игр и принятия решений

полезность, чем реальную величину платежей. Для демонстрации этого предпо­ложим следующее. Существует шанс 50 на 50, что инвестиция в 20 ООО долл. или принесет прибыль в 40 ООО долл., или будет полностью потеряна. Соответствующая ожидаемая прибыль равна 40000 х 0,5 - 20000 х 0,5 = 10000 долл. Хотя здесь ожи­дается прибыль в виде чистого дохода, разные люди могут по-разному интерпрети­ровать полученный результат. Инвестор, который идет на риск, может вложить деньги, чтобы с вероятностью 50 % получить прибыль в 40 000 долл. Наоборот, ос­торожный инвестор может не выразить желания рисковать потерей 20 000 долл. С этой точки зрения очевидно, что разные индивидуумы проявляют разное отно­шение к риску, т.е. они проявляют разную полезность по отношению к риску.

Определение полезности является субъективным. Оно зависит от нашего отноше­ния к риску. В этом разделе мы представляем систематизированную процедуру чи­словой оценки отношения к риску лица, принимающего решение. Конечным резуль­татом является функция полезности, которая занимает место реальных денег.

В примере, приведенном выше, наилучший платеж равен 40 000 долл., а наи­худший --20 000 долл. Мы устанавливаем произвольную (но логически обос­нованную) шкалу полезности U, изменяющуюся от 0 до 100, где 0 соответствует полезности -20 000, а 100 — 40000, т.е. [/(-20000) = 0 и [/(40000) = 100. Далее определяем полезность в точках между -20000 и 40000 для определения общего вида функции полезности.

Если отношение лица, принимающего решение, беспристрастно к риску, то ре­зультирующая функция полезности является прямой линией, соединяющей точки (0, -20000) и (100, 40000). В этом случае как реальные деньги, так и их полезность дают совпадающие решения. В более реальных ситуациях функция полезности мо­жет принимать другой вид, отражающий отношение к риску лица, принимающего решение. На рис. 14.7 иллюстрируется вид функции полезности для трех индиви­дуумов X, Y и Z. Индивидуум X не расположен к риску (осторожен), так как прояв­ляет большую чувствительность к потере, чем к прибыли. Индивидуум Z — противо­положность в этом отношении индивиду X; он настроен на риск. Это следует из того, что для индивидуума X при изменении в 10 000 долл. вправо и влево от точки, соот­ветствующей 0 долларов, увеличение прибыли изменяет полезность на величину ab, которая меньше изменения полезности be, обусловленной потерями такой же вели­чины, т.е. ab < be. В то же время такие же изменения в ±10000 долл., относящиеся к индивидууму Z, обнаруживают противоположное поведение; здесь de > ef. Далее, ин­дивидуум У является нейтральным к риску, так как упомянутые изменения порож­дают одинаковые изменения полезности. В общем случае индивидуум может быть как не расположен к риску, так и настроен на риск, в зависимости от суммы риска. В этом случае соответствующая кривая полезности будет иметь вид удлиненной буквы S.

Кривые полезности, аналогичные изображенным на рис. 14.7, определены с по­мощью количественного показателя, характеризующего отношение к риску лица, принимающего решение, для различных значений уровня реальных денег в пределах установленного интервала. Так в рассмотренном примере установленным интервалом является (-20000,40000), соответствующая полезность изменяется в интервале (0,100). Необходимо определить полезность, соответствующую таким промежуточ­ным значениям, как например, -10 000, 0, 10 000, 20 000 или 30 000. Соответствую­щая процедура построения функции полезности начинается с того, что организовы­вается лотерея для определения суммы реальных денег х, для которой ожидаемое значение полезности будет вычислено по следующей формуле.

Щх) = р[/(-20000) + (1 т р)С/(40000) = Ор + 100(1 - р) = 100 - ЮОр, 0 <р < 1.

14.2. Принятие решений в условиях риска 573

Тысячи долларов

Рис. 14.7. Функция полезности для лиц, по-разному относящихся к риску

Для определения значения U(x) просят лицо, принимающее решение, сообщить свое предпочтение между гарантированной наличной суммой х и возможностью сыграть в лотерею, в которой с вероятностью р реализуется проигрыш в сумме 20000 долл. и с вероятностью 1 - р имеет место выигрыш в 40000 долл. При этом под предпочтением понимается выбор значения "нейтральной" вероятности р, при котором, с точки зрения лица, принимающего решение, возможности сыграть в ло­терею и получить гарантированную сумму х являются одинаково привлекатель­ными. Например, если х = 20000 долл., лицо, принимающее решение, может зая­вить, что гарантированные 20000 долл. наличными и лотерея одинаково привлекательны при р = 0,8. В этом случае вычисляется полезность для х = 20000 по следующей формуле.

(7(20000) = 100 - 100 х 0,8 = 20.

Эта процедура продолжается до тех пор, пока не будет получено достаточное ко­личество точек (х, Щх)) для определения формы функции полезности. Затем мож­но определить искомую функцию полезности путем регрессионного анализа или просто линейной интерполяции между полученными точками.

Хотя здесь применяется количественная процедура для определения функции по­лезности, сам подход далек от того, чтобы быть научно обоснованным. То, что процеду­ра полностью определяется мнением лица, принимающего решение, порождает сомне­ния относительно надежности описанного процесса. Процедура, в частности, неявно предполагает, что лицо, принимающее решение, является рационально мыслящим — требование, которое не всегда может быть согласовано с вариациями в поведении и настроении, что является типичным для человеческой личности. В этом отношении лицо, принимающее решение, должно придерживаться концепции полезности в ши­роком смысле, в соответствии с которой денежные величины не должны быть единст­венным решающим фактором в теории принятия решений.

Глава 14. Теория игр и принятия решений

УПРАЖНЕНИЯ 14.2.3

1. Допустим, вы — студент университета штата Арканзас, и имеете сильное желание присутствовать на следующем баскетбольном матче. Проблема в том, что входной билет стоит 10 долл., а у вас есть лишь 5 долл. Вы можете рискнуть 5 долл. в игре в покер с шансами 50 на 50 удвоить свою сумму или совсем ее проиграть.

a) Будете ли вы, исходя из реальной стоимости денег, искушать судьбу, иг­рая в покер?

b) Учитывая ваше сильное желание присутствовать на матче, переведите на­личные деньги в функцию полезности.

c) Основываясь на функции полезности, которую вы построили, примете ли вы участие в игре в покер?

2. Семья переехала в местность, где возможны землетрясения, и собирается по­строить дом. Решается вопрос, стоит ли строить дом в соответствии с высо­кими стандартами, рассчитанными на сейсмическую зону. Строительство дома в соответствии с такими стандартами обойдется в 850 ООО долл., а без их учета — в 350 000 долл. В случае землетрясения (его вероятность равна 0,001) восстановление дома, построенного без соответствующих стандартов, обойдется в 900 000 долл. Примените в этой ситуации рассмотренную выше процедуру использования лотереи, предполагая, что шкала полезности из­меняется от 0 до 100.

3. Инвестиция в 10 000 долл. в предприятие с высоким уровнем риска имеет шанс 50 на 50 увеличить эту сумму до 14 000 долл. на протяжении следую­щего года либо уменьшить ее до 8 000 долл. Это значит, что чистый доход со­ставит либо 4000 долл., либо -2000 долл.

a) Принимая позицию нейтрального к риску инвестора и шкалу полезности от 0 до 100, определите полезность 0 долл. чистого дохода и соответст­вующую "нейтральную" вероятность.

b) Пусть два инвестора А и В определили следующие "нейтральные" веро­ятности.

Вероятность

Чистая прибыль (долл.)	Инвестор А	Инвестор В
-2000	1,00	1,00
-1000	0,30	0,90
	0,20	0,80
	0,15	0,70
	0,10	0,50
	0,05	0,40
	0,00	0,00

Нарисуйте графики функций полезности для инвесторов А и В и охарак­теризуйте их отношение к риску.

с) Пусть инвестор А может вложить деньги в одно из двух рискованных предприятий: I или И. Инвестиция в предприятие I может принести прибыль в сумме 3000 долл. с вероятностью 0,4 или убыток в 1000 долл.

14.3. Принятие решений в условиях неопределенности

с вероятностью 0,6. Инвестиция в предприятие II может принести при­быль в 2000 долл. с вероятностью 0,6 или вовсе не принести прибыли с ве­роятностью 0,4. Используя функцию полезности инвестора А, построен­ную в предыдущем пункте, и критерий ожидаемой полезности, определите предприятие, которое следует выбрать инвестору А. Каково ожидаемое денежное значение, соответствующее выбранному предпри­ятию (используйте линейную интерполяцию функции полезности)?

d) Повторите упражнение предыдущего пункта для инвестора В.

14.3. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

Принятие решений в условиях неопределенности, как и в условиях риска, тре­бует определения альтернативных действий, которым соответствуют платежи, за­висящие от (случайных) состояний природы. Матрицу платежей в задаче принятия решений с т возможными действиями и п состояниями природы можно предста­вить следующим образом.

	S1	s2	sn
ai	Kai, si)	Kai, s2)	v(a:, s„)
аг	i/(a2, si)	i/(a2, s2)	Ka2, s„)
	Kam, si)	v(am, s2)	Kam, sn)

Элемент а, представляет i-e возможное решение, а элемент s_t— j-e состояние природы. Плата (или доход), связанная с решением а, и состоянием s_t, равна t>(a,, s_;).

Отличие между принятием решений в условиях риска и неопределенности со­стоит в том, что в условиях неопределенности вероятностное распределение, соот­ветствующее состояниям s_;, /=1,2, п, либо неизвестно, либо не может быть оп­ределено. Этот недостаток информации обусловил развитие следующих критериев для анализа ситуации, связанной с принятием решений.

1. Критерий Лапласа.

2. Минимаксный критерий.

3. Критерий Сэвиджа.

4. Критерий Гурвица.

Эти критерии отличаются по степени консерватизма, который проявляет индиви­дуум, принимающий решение, перед лицом неопределенности.

Критерий Лапласа опирается на принцип недостаточного основания⁴, который гласит, что, поскольку распределение вероятностей состояний P(s_/) неизвестно, нет причин считать их различными. Следовательно, используется оптимистическое предположение, что вероятности всех состояний природы равны между собой, т.е. ?{s,} = P{s₂} = ... = P{sJ = 1/п. Если при этом у(а,, s_y) представляет получаемую при­быль, то наилучшим решением является то, которое обеспечивает

⁴ Этот принцип впервые сформулирован Я. Бернулли. —

Прим. перев.

Глава 14. Теория игр и принятия решений

Если величина v(a_t, s_y) представляет расходы лица, принимающего решение, то оператор "max" заменяется на "min".

Максиминный (минимаксный) критерий основан на консервативном осторож­ном поведении лица, принимающего решение, и сводится к выбору наилучшей альтернативы из наихудших. Если величина v(a_t, s_y) представляет получаемую при­быль, то в соответствии с максиминным критерием в качестве оптимального выби­рается решение, обеспечивающее

naxjminv^.Sj jj.

Если величина v(a_t, s_f) представляет потери, используется минимаксный критерий, который определяется следующим соотношением.

ггап|таху(а,,5^|.

Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путем замены матрицы платежей (выигрышей или проигрышей) v(a_t, s) мат­рицей потерь ria_t, s}, которая определяется следующим образом.

max{v(a_t,5_;)}-v(a,.,s_;), если v-доход, v^a^Sj)-min{v(e_t,S;)}, если v-потери.

Чтобы показать, как критерий Сэвиджа "смягчает" минимаксный (максиминный) критерий, рассмотрим следующую матрицу платежей и(а , s.):

	S1	S2	Максимум строк
ai	11 ООО		11 000
a2	10 000	10 000	10 000 <— минимакс

Применение минимаксного критерия приводит к тому, что решение а₂ с фикси­рованными потерями в 10000 долл. является предпочтительным. Однако можно вы­брать и a_v так как в этом случае существует возможность потерять лишь 90 долл., ес­ли реализуется состояние s₂, при потенциальном выигрыше 11 000 долл.

Посмотрим, какой результат получится, если в минимаксном критерии вместо матрицы платежей v(a_jt s^) использовать матрицу потерь ria^s}.

	S1	S2	Максимум строк
ai			1000 <- минимакс
аг

Как видим, минимаксный критерий, применяемый к матрице потерь, приводит к выбору решения а, в качестве предпочтительного.

Рассмотрим теперь критерий Гурвица. Этот критерий охватывает ряд различных подходов к принятию решений — от наиболее оптимистичного до наиболее пессими­стичного (консервативного). Пусть 0 < а< 1 и величины v(a_lt представляют доходы. Тогда решению, выбранному по критерию Гурвица, соответствует

14.3. Принятие решений в условиях неопределенности

тах|атаху(а;,^_у) + (1 - a) min v^.s^j.

Параметр а— показатель оптимизма. Если ог= 0, критерий Гурийца становится кон­сервативным, так как его применение эквивалентно применению обычного мини­максного критерия. Если а= 1, критерий Гурвица становится слишком оптимистич­ным, ибо рассчитывает на наилучшие из наилучших условий. Мы можем конкретизировать степень оптимизма (или пессимизма) надлежащим выбором вели­чины огиз интервала [0, 1]. При отсутствии ярко выраженной склонности к оптимиз­му или пессимизму выбор а= 0,5 представляется наиболее разумным.

Если величины и(а,, s.) представляют потери, то критерий принимает следую­щий вид:

rranjarnin v(a_;,sj + (1 -a)maxv(a,,s_yH.

Пример 14.3.1

Национальная школа выживания подбирает место для строительства летнего лагеря в центре Аляски в целях тренировки людей на выживание в условиях дикой приро­ды. Школа считает, что число участников сбора может быть 200, 250, 300 или 350 человек. Стоимость летнего лагеря будет минимальной, поскольку он строится для удовлетворения только определенных небольших потребностей. Отклонения в сторо­ну уменьшения или увеличения относительно идеальных уровней потребностей вле­кут за собой дополнительные затраты, обусловленные строительством избыточных (неиспользуемых) мощностей или потерей возможности получить прибыль в случае, когда некоторые потребности не удовлетворяются. Пусть переменные a-a_t представ­ляют возможные размеры лагеря (на 200, 250, 300 или 350 человек), а переменные 5,-5₄ — соответствующее число участников сбора. Следующая таблица содержит мат­рицу стоимостей (в тысячах долларов), относящуюся к описанной ситуации.

	S1	s2	S3	S4
ai
а2
аз
а>

Описанная ситуация анализируется с точки зрения четырех рассмотренных выше критериев.

Критерий Лапласа. При заданных вероятностях P{s^ = 1/4, j= 1, 2, 3, 4, ожидае­мые значения затрат для различных возможных решений вычисляются следую­щим образом.

М{а_х) = (1/4)(5 + 10 + 18 + 25) = 14 500,

М{а_г) = (1/4)(8 + 7 + 12 + 23) = 12 500 <- Оптимум,

М{а₃) = (1/4)(21 + 18 + 12 + 21) = 18 000,

M{a_t) = (1/4)(30 + 22 + 19 + 15) = 21 500.

578 Глава 14. Теория игр и принятия решений

Минимаксный критерий. Этот критерий использует исходную матрицу стоимостей.

Si S2 S3 S4 Максимум строк

a-i
а2
а3						21 <- минимакс
ад
Критерий Сэвиджа. Матрица потерь определяется посредством вычитания чисел 5, 7, 12 и 15 из элементов столбцов от первого до четвертого соответственно. Следова­тельно,
	S1	S2	S3	s4		Максимум строк
ai
						8 <— минимакс
аэ
ад
Критерий Гурвица. Результаты вычислений содержатся в следующей таблице.
Альтернатива Минимум строк	Максимум строк	«(минимум строки) + (1 - а)(максимум строки)
ai						25 - 20а
аг						23-16а
аз						21 -9а
ад						30-15а

Используя подходящее значение для а, можно определить оптимальную альтерна­тиву. Например, при а= 0,5 оптимальными являются либо альтернатива а,, либо а₂, тогда как при а= 0,25 оптимальным является решение а₃.

Реализация в Excel критериев принятия решений в условиях неопределенности.

Шаблон Excel chl4UncertainlyDecision.xls можно использовать для вычисления всех критериев, описанных выше. Основой вычислений служит матрица затрат (диапазон В9:К19). Если надо использовать матрицу выигрышей, то все элементы этой матрицы надо умножить на -1. Максимальный размер матриц 10x10. На рис. 14.8 показано применение этого шаблона к данным примера 14.3.1.

УПРАЖНЕНИЯ 14.3

1. Хенк — прилежный студент, который обычно получает хорошие отметки благодаря, в частности, тому, что имеет возможность повторить материал в ночь перед экзаменом. Перед завтрашним экзаменом Хенк столкнулся с не­большой проблемой. Его сокурсники организовали на всю ночь вечеринку, в которой он хочет участвовать. Хенк имеет три альтернативы:

а₁ — участвовать в вечеринке всю ночь,

а₂ — половину ночи участвовать в вечеринке, а половину — учиться, а₃ — учиться всю ночь.

14.3. Принятие решений в условиях неопределенности

	А	В		D E	L	M	N	Q
	Decision Under Uncertainty
	Enter x to select method:		Output Results
	Laplace	X
	Minimax	X
	Savage	X
	Hurwicz	X	Alpha= 10.5		Optimum strategies
	Input (cost) Matrix: Maximum size = (10x10)	a2	a3	a2	a2
			s2	s3 s4	Laplace	Minimax	Savage	Hurwicz
	a1			18 25	14 5
	a2			12 23	12 5
И	a3			12 21
	a4			19 15	21 5			22 5

Рис. 14.8. Решение в Excel примера 14.3.1

Профессор, принимающий завтрашний экзамен, непредсказуем, и экзамен может быть легким (sj, средним (s₂) или трудным (s₃). В зависимости от сложности экзамена и времени, затраченного Хенком на повторение, можно ожидать следующие экзаменационные баллы.

Si S2 s₃

ai
а2
а3

a) Порекомендуйте Хенку, какой выбор он должен сделать (основываясь на каждом из четырех критериев принятия решений в условиях неопреде­ленности).

b) Предположим, что Хенк более заинтересован в оценке (в буквенном вы­ражении), которую он получит на экзамене. Буквенным оценкам от А до D, означающим сдачу экзамена, соответствует 90, 80, 70 и 60 баллов. Иначе при числе баллов ниже 60 студент получает оценку F, которая сви­детельствует о том, что экзамен не сдан. Изменит ли такое отношение к оценкам выбор Хенка?

2. В приближении посевного сезона фермер Мак-Кой имеет четыре альтернативы:

а, — выращивать кукурузу,

а₂ — выращивать пшеницу,

a_s — выращивать соевые бобы,

а₄ — использовать землю под пастбища.

Платежи, связанные с указанными возможностями, зависят от количества осадков, которые условно можно разделить на четыре категории:

Sj — сильные осадки,

s₂ — умеренные осадки,

s_s — незначительные осадки,

s₄ — засушливый сезон.

Платежная матрица (в тыс. долл.) оценивается следующим образом.

Глава 14. Теория игр и принятия решений

	S1	s2	S3	S4
	-20			-5
32
	-50			-10
ад

Что должен посеять Мак-Кой?

3. Один из N станков должен быть выбран для изготовления Q единиц опреде­ленной продукции. Минимальная и максимальная потребность в продукции равна Q* и Q соответственно. Производственные затраты ТС, на изготовле­ние Q единиц продукции на станке i включают фиксированные затраты К₁ и удельные затраты с, на производство единицы продукции и выражаются формулой ТС_: = К, + c/Q.

a) Решите задачу с помощью каждого из четырех критериев принятия ре­шений в условиях неопределенности.

b) Решите задачу при следующих данных, предполагая, что 1000 < Q < 4000.

Станок /'	К, (долл.)	с, (долл.)

14.4. ТЕОРИЯ ИГР

В теории игр рассматриваются ситуации, связанные с принятием решений, в кото­рых два разумных противника имеют конфликтующие цели. К числу типичных при­меров относится рекламирование конкурирующих товаров и планирование военных стратегий противоборствующих армий. Эти ситуации принятия решений отличаются от рассмотренных ранее, где природа не рассматривается в роли недоброжелателя.

В игровом конфликте участвуют два противника, именуемые игроками, каждый из которых имеет некоторое множество (конечное или бесконечное) возможных вы­боров, которые называются стратегиями. С каждой парой стратегий связан платеж, который один из игроков выплачивает другому. Такие игры известны как игры двух лиц с нулевой суммой, так как выигрыш одного игрока равен проигрышу другого. В такой игре достаточно задать результаты в виде платежей для одного из игроков. При обозначении игроков через А и В с числом стратегий тип соответственно игру обычно представляют в виде матрицы платежей игроку А:

	в,	Вг	Вп
А,			Зщ
Аг		S22	32л
Am	Зт1	Sm2	Зтл

Такое представление матричной игры означает, что если игрок А использует стратегию /, а игрок В — стратегию j, то платеж игроку А составляет a_tj и, следова­тельно, игроку В--а_ц.

14.4. Теория игр

14.4.1. Оптимальное решение игры двух лиц с нулевой суммой

Поскольку игры берут свое начало в конфликте интересов, оптимальным решени­ем игры является одна или несколько таких стратегий для каждого из игроков, при этом любое отклонение от данных стратегий не улучшает плату тому или другому иг­року. Эти решения могут быть в виде единственной чистой стратегии или нескольких стратегий, которые являются смешанными в соответствии с заданными вероятно­стями. Рассматриваемые ниже примеры демонстрируют перечисленные ситуации.

Пример 14.4.1

Две компании А и В продают два вида лекарств против гриппа. Компания А реклами­рует продукцию на радио (АЛ, телевидении (А₂) и в газетах (АЛ. Компания В, в допол­нение к использованию радио (ВЛ, телевидения (ВЛ и газет (В,), рассылает также по почте брошюры (5₄). В зависимости от умения и интенсивности проведения рек­ламной кампании, каждая из компаний может привлечь на свою сторону часть клиентов конкурирующей компании. Приведенная ниже матрица характеризует процент клиентов, привлеченных или потерянных компанией А.

Максимумы столбцов

	в.	Вг	Вз	в4	Минимумы строк
А,		-2		-3	-3
Аг					5 максимин
Аз	-2		-9		-9

минимакс

Решение игры основано на обеспечении наилучшего результата из наихудших для каждого игрока. Если компания А выбирает стратегию А_х, то, независимо от того, что предпринимает компания В, наихудшим результатом является потеря компанией А 3 % рынка в пользу компании В. Это определяется минимумом элементов первой строки матрицы платежей. Аналогично при выборе стратегии А₂ наихудшим исходом для компании А является увеличение рынка на 5 % за счет компании В. Наконец, наи­худшим исходом при выборе стратегии А₃ является потеря компанией А 9 % рынка в пользу компании В. Эти результаты содержатся в столбце "Минимумы строк". Чтобы достичь наилучшего результата из наихудших, компания А выбирает стратегию А₂, так как она соответствует наибольшему элементу столбца "Минимумы строк".

Рассмотрим теперь стратегии компании В. Так как элементы матрицы являются платежами компании А, критерий наилучшего результата из наихудших для компании В соответствует выбору минимаксного значения. В результате приходим к выводу, что выбором компании В является стратегия В₂.

Оптимальным решением в игре является выбор стратегий А₂ и В₂, т.е. обеим компа­ниям следует проводить рекламу на телевидении. При этом выигрыш будет в пользу компании А, так как ее рынок увеличится на 5 %. В этом случае говорят, что цена игры равна 5 % и что компании А и В используют стратегии, соответствующие седловой точке.

Глава 14. Теория игр и принятия решений

Решение, соответствующее седловой точке, гарантирует, что ни одной компании нет смысла пытаться выбрать другую стратегию. Действительно, если компания В переходит к другой стратегии (/?,, В_% или B_t), то компания А может сохранить свой выбор стратегии А_г, что приведет к большей потере рынка компанией В (6 или 8 %). По тем же причинам компании А нет резона использовать другую стратегию, ибо если она применит, например, стратегию А₃, то компания В может использовать свою стратегию В₃ и увеличить свой рынок на 9 % . Аналогичные выводы имеют ме­сто, если компания А будет использовать стратегию А_х.

Оптимальное решение игры, соответствующее седловой точке, не обязательно должно характеризоваться чистыми стратегиями. Вместо этого оптимальное реше­ние может требовать смешивания случайным образом двух или более стратегий, как это сделано в следующем примере.

Пример 14.4.2

Два игрока А и В играют в игру, основанную на подбрасывании монеты. Игроки од­новременно и независимо друг от друга выбирают герб (Г) или решку (Р). Если ре­зультаты двух подбрасываний монеты совпадают (т.е. ГГ или РР), то игрок А полу­чает один доллар от игрока В. Иначе игрок А платит один доллар игроку В.

Следующая матрица платежей игроку А показывает величины минимальных эле­ментов строк и максимальных элементов столбцов, соответствующих стратегиям обоих игроков.

	Вг	ВР	Минимумы строк
Аг		-1	-1
Ар	-1		-1
Максимумы столбцов

Максиминная и минимаксная величины (цены) для этой игры равны -1 долл. и 1 долл. соответственно. Так как эти величины не равны между собой, игра не имеет решения в чистых стратегиях. В частности, если игрок А использует стратегию А_г, игрок В выберет стратегию В_р, чтобы получить от игрока А один доллар. Если это случится, игрок А может перейти к стратегии А_р, чтобы изменить исход игры и получить один доллар от игрока В. Постоянное искушение каждого игрока пе­рейти к другой стратегии указывает на то, что решение в виде чистой стратегии неприемлемо. Вместо этого оба игрока должны использовать надлежащую слу­чайную комбинацию своих стратегий. В рассматриваемом примере оптимальное значение цены игры находится где-то между максиминной и минимаксной цена­ми для этой игры:

максиминная (нижняя) цена < цена игры < минимаксная (верхняя) цена.

Следовательно, в данном случае цена игры должна лежать в интервале [-1,1], из­меряемом в долларах.

14.4. Теория игр

УПРАЖНЕНИЯ 14.4.1

1. Определите решение, определяемое седловой точкой, соответствующие чис­тые стратегии и цену игры для следующих игр, в которых платежи заданы для игрока А.

а)

	е,	е2	Вз	е4
Аг
Аз

Ь)

	Bi	Bi	Вз	е4
Ау		-4	-5
Аг	-3	-4	-9	-2
Аз			-8	-9
Ал			-9

2. В следующих играх заданы платежи игроку А. Укажите область значений для параметров р и q, при которых пара (2, 2) будет седловой точкой в каждой игре.

а)

Bi Вг е₃

4i		Я
А>	Р
	е,	е2	е3
А
Аг			Я
Аз		Р

3. Укажите область, которой принадлежит цена игры в каждом из следующих случаев, предполагая, что платежи заданы для игрока А.

а)

	В,		бз	е4
-4.1
Аг
Аз	-5	-2		-3
Ал			-2	-5

Глава 14. Теория игр и принятия решений

Ь)

с)

	е.		е3	е4
	-1
Аг	-2
Аз
А*		-2

d)

	е.		Вз	е4
				-6
		-9	-2

4. Две фирмы производят два конкурирующих товара. Каждый товар в на­стоящее время контролирует 50 % рынка. Улучшив качество товаров, обе фирмы собираются развернуть рекламные кампании. Если они не будут этого делать, то существующее состояние рынка не изменится. Однако если какая-либо фирма будет более активно рекламировать свои товары, то другая фир­ма потеряет соответствующий процент своих потребителей. Исследование рынка показывает, что 50 % потенциальных потребителей получают инфор­мацию посредством телевидения, 30 % — через газеты и 20 % — по радио.

a) Сформулируйте задачу в виде игры двух лиц с нулевой суммой и выберите подходящие средства рекламы для каждой фирмы.

b) Укажите интервал значений, которому принадлежит цена игры. Может ли каждая фирма действовать с единственной чистой стратегией?

5. Пусть a_tj — (г, /)-й элемент платежной матрицы с т стратегиями игрока А и л стратегиями игрока В. Элементы платежной матрицы представляют собой платежи игроку А. Докажите, что

max min а,, < min max а,,.

14.4.2. Решение матричных игр в смешанных стратегиях

Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Графический метод применим для решения игр, в которых хоть один игрок имеет две чистые страте­гии. Этот метод интересен в том плане, что графически объясняет понятие седловой точки. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.

Графическое решение игр. Рассмотрим игру 2 х п, в которой игрок А имеет две стратегии.

14.4. Теория игр

	У1	у2	У"
	е.	Вг	Вп
Хъ Ау	an		Зщ
1 - хь А2			32л

Игра предполагает, что игрок А смешивает стратегии А₁ и А₂ с соответствующи­ми вероятностями я, и 1 - я,, 0 < 1. Игрок В смешивает стратегии B_lt В₂, В_п с вероятностями (/,, у_г, (/„, где i/.>0, ;= 1, 2, п, и у, + j/₂ + ... + (/„ = 1. В этом случае ожидаемый выигрыш игрока А, соответствующий j-й чистой стратегии иг­рока В, вычисляется в виде

(^аи ~ ^а2,) ^xi ~ ^агг J⁼¹<².....^п-

Следовательно, игрок А ищет величину х_х, которая максимизирует минимум ожи­даемых выигрышей

maxmin j(a,_y -a_2j}x_l -а₂,У

Пример 14.4.3

Рассмотрим следующую игру 2x4, в которой платежи выплачиваются игроку Л.

В Вг Вз 64

А '

Аг

2 2 3 -1

4 3 2 6

Игра не имеет решения в чистых стратегиях, и, следовательно, стратегии должны быть смешанными. Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, приведены в следующей таблице.

Чистые стратегии игрока В	Ожидаемые выигрыши игрока А
	-2xi + 4
	-*1 + 3
	* +2
	-7*1 + 6

На рис. 14.9 изображены четыре прямые линии, соответствующие чистым страте­гиям игрока В. Чтобы определить наилучший результат из наихудших, построена нижняя огибающая четырех указанных прямых (изображенная на рисунке толстыми линейными сегментами), которая представляет минимальный (наихудший) выиг­рыш для игрока А независимо от того, что делает игрок В. Максимум (наилучшее) нижней огибающей соответствует максиминному решению в точке х - 0,5 . Эта точка

определяется пересечением прямых 3 и 4. Следовательно, оптимальным решением для игрока А является смешивание стратегий А_х и А₂ с вероятностями 0,5 и 0,5 соот­ветственно. Соответствующая цена игры v определяется подстановкой х, = 0,5 в уравнение либо прямой 3, либо 4, что приводит к следующему.

Глава 14. Теория игр и принятия решений

-^ + 2 = -^ из уравнения прямой 3, -7^| + 6 = -|- из уравнения прямой 4.

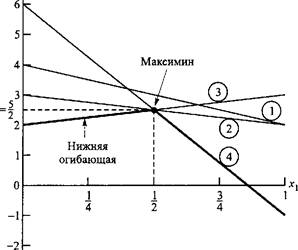
Рис. 14.9. Графическое решение игры двух лиц с нулевой суммой из примера 14.4.3

Оптимальная смешанная стратегия игрока В определяется двумя стратегиями, ко­торые формируют нижнюю огибающую графика. Это значит, что игрок В может смешивать стратегии В₃ и В₄, в этом случае у, =у₂ = О и у₄ = 1 - у₃. Следовательно, ожидаемые платежи игрока В, соответствующие чистым стратегиям игрока А, имеют такой вид.

Чистые стратегии игрока А Ожидаемые платежи игрока В

1 4у₃ - 1

2 -4у₃ + 6

Наилучшее решение из наихудших для игрока В представляет собой точку мини­мума верхней огибающей заданных двух прямых (построение прямых и определе­ние верхней огибающей будет для вас поучительным). Эта процедура эквивалентна решению уравнения

4_>3-1 = -4у₃ + 6.

Его решением будету₃ = 7/8, что определяет цену игры v = 4 х (7/8) - 1 = 5/2.

Таким образом, решением игры для игрока А является смешивание стратегий А, иА₂с равными вероятностями 0,5 и 0,5, а для игрока В — смешивание стратегий В_г и В₄ с вероятностями 7/8 и 1/8. (В действительности игра имеет альтернативное решение для игрока В, так как максиминная точка на рис. 14.9 определяется более чем двумя прямыми. Любая выпуклая линейная комбинация этих альтернативных решений также является решением задачи.)

14.4. Теория игр

Для игры, в которой игрок Л имеет т стратегий, а игрок В — только две, реше­ние находится аналогично. Главное отличие состоит в том, что здесь строятся гра­фики функций, представляющих ожидаемые платежи второго игрока, соответст­вующие чистым стратегиям игрока А. В результате ведется поиск минимаксной точки верхней огибающей построенных прямых.

УПРАЖНЕНИЯ 14.4.2

1. Решите графически игру с подбрасыванием монет из примера 14.4.2.

2. Робин часто ездит между двумя городами. При этом есть возможность вы­брать один из двух маршрутов: маршрут А представляет собой скоростное шоссе в четыре полосы, маршрут В — длинную обдуваемую ветром дорогу. Патрулирование дорог осуществляется ограниченным числом полицейских. Если все полицейские расположены на одном маршруте, Робин с ее страст­ным желанием ездить очень быстро, несомненно, получит штраф в 100 долл. за превышение скорости. Если полицейские патрулируют на двух маршру­тах в соотношении 50 на 50, то имеется 50 % -ная вероятность, что Робин по­лучит штраф в 100 долл. на маршруте А и 30 % -ная вероятность, что она по­лучит такой же штраф на маршруте В. Кроме того, маршрут В длиннее, поэтому бензина расходуется на 15 долл. больше, чем на маршруте А. Опре­делите стратегию как для Робин, так и для полиции.

3. Решите графически следующие игры, в которых платежи выплачиваются игрокуА.

а)

в.

Вг

Ау Аг -3 4

ъ)

	By	Вг
Ау
Аг
Аз

4. Дана следующая игра двух лиц с нулевой суммой.

	By	Вг	Вз
	5,0	50,0	50,0
Аг	1,0	1,0	0,1
Аз	10,0	1,0	10,0

a) Проверьте, что смешанные стратегии с вероятностями (1/6,0,5/6) для игрока А и с вероятностями (49/54, 5/54, 0) для игрока В являются опти­мальными, и определите цену игры.

b) Покажите, что цена игры равна

3 3

Глава 14. Теория игр и принятия решений

Решение матричных игр методами линейного программирования. Теория игр находится в тесной связи с линейным программированием, так как любую конеч­ную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования и наоборот. Дж. Данциг [3] отмечает, что, когда в 1947 году создатель теории игр Дж. фон Нейман впервые ознакомился с симплекс-методом, он сразу установил эту взаимосвязь и обратил особое внимание на концепцию двой­ственности в линейном программировании. Этот раздел иллюстрирует решение матричных игр методами линейного программирования.

Оптимальные значения вероятностей x_t, i = 1, 2, т, игрока А могут быть оп­ределены путем решения следующей максиминной задачи.

тт т

/=1 (=1 1=1

х_х + х₂ + ... + х_т = 1, х. > О, i = 1, 2.....т.

Чтобы сформулировать эту задачу в виде задачи линейного программирования, положим

v = min X^-Z^^/'-'Zv.

Отсюда вытекает, что

Za*.-^v- у=1.2,..-, л.

Следовательно, задача игрока А может быть записана в виде

максимизировать z = v

при ограничениях

v-^Vi-°- 7 = 1-2,...,/!,

i=i

x_t + х_г + ... + х_т = 1,

х, > О, i = l, 2, т,

v не ограничена в знаке. Отметим последнее условие, что цена игры v может быть как положительной, так и отрицательной.

Оптимальные стратегии y_v у₂, у_п игрока В определяются путем решения задачи

limax Z^y-IX^.....1ХЛ

Vj = 1 j=1 у = 1 ,

mm j max

Уг + У_г+ ■■■+У„ = 1> y>0, /-1,2.....re.

Используя процедуру, аналогичную приведенной выше для игрока А, приходим к выводу, что задача для игрока В сводится к следующему.

Минимизировать w — v

при ограничениях

V -

7 = 1

ZV,^⁰' ' = 1.2...., п

-л

у,+у_г+... +(/„ = !,

14.4. Теория игр

i/.>0, ; = 1, 2, п,

v не ограничена в знаке.

Две полученные задачи оптимизируют одну и ту же (не ограниченную в знаке) переменную и, которая является ценой игры. Причиной этого служит то, что зада­ча игрока В является двойственной к задаче игрока А (вам предлагается доказать это утверждение в упражнении 14.4.3.5, используя определение двойственности из главы 4). Это означает, что оптимальное решение одной из задач автоматически определяет оптимальное решение другой.

Пример 14.4.4

Решим следующую матричную игру методами линейного программирования.

	В,	Вг	Вз	Минимумы строк
Ау		-1	-3	-3
А2	-2		-1	-2
Аз	-5	-6		-6
Максимумы столбцов

Значение цены игры v находится между -2 и 2. Задача линейного программирования для игрока А

Максимизировать z = v

при ограничениях

v - За-j + 2х₂ + 5лг₃ < О, v + л-j - 4х₂ + 6х₃ < О, v + 3x₁+x₂-2x₃<0,

x_v х₂, х₃ > О,

v не ограничена в знаке. Оптимальным решением является х_г = 0,39, х₂ = 0,31, х₃ = 0,29 и v = -0,91. Задача линейного программирования для игрока В

Минимизировать z = v

при ограничениях

о-3у,+у₂ + 3у₃>0, и + 2_У1-4у₂+у₃>0, v + 5_yi + 6y₂-2y₃>0,

v не ограничена в знаке. Оптимальным решением является у, = 0,32, у₂ = 0,08, у₃ = 0,60 и v = -0,91.

Глава 14. Теория игр и принятия решений

В программе TORA для решения игр двух игроков с нулевой суммой надо выбрать команду Zero-sum GamesOSolve^LP-based (Игры с нулевой суммой^Решить^Как задачу ЛП). На рис. 14.10 показан результат решения задачи примера 14.4.4 (файл ch 14ToraGamesEx 14-4-4).

TORA D:WoikTordFileich14ToraGarnesfx14 4 4 Itf

DECISION ANALYSIS USING GAMES

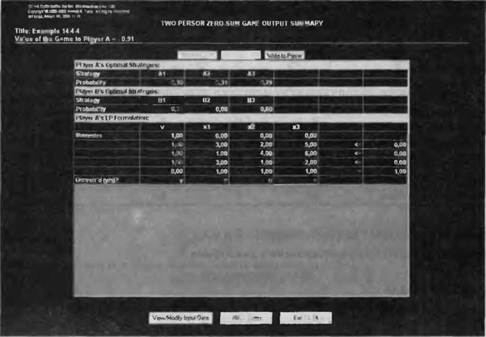
Рис. 14.10. Решение программой TORA игры двух игроков с нулевой суммой из примера 14.4.4

УПРАЖНЕНИЯ 14.4.3

1. На загородном пикнике две команды, по два человека в каждой, играют в прятки. Есть четыре места, где можно спрятаться (А, Б, В и Г), и два члена прячущейся команды могут спрятаться каждый отдельно в любых двух из че­тырех мест. Затем другая команда имеет возможность проверить любые два места. Команда, которая ищет, получает премию, если будут обнаружены оба участника прячущейся команды, если же не обнаружен ни один участник, то она выплачивает премию. Иначе игра заканчивается вничью.

a) Сформулируйте задачу в виде игры двух лиц с нулевой суммой.

b) Определите оптимальные стратегии и цену игры.

2. Университетские команды UA и DU определяют свои стратегии игры в на­циональном чемпионате по баскетболу для колледжей. Оценивая возможно­сти своих "запасных скамеек", каждый тренер разработал по четыре вариан­та замены игроков на протяжении игры. Способность каждой команды выполнять двух-, трехочковые и штрафные броски является основным фак-

Литература

тором, определяющим результат игры. Приведенная ниже таблица содер­жит очки чистого выигрыша команды UA на протяжении одного владения мячом в зависимости от стратегий, планируемых каждой командой.

	DU1	DU2	DU3	DU4
UAi		-2
UA2			-3
UA3	-1		-2
UA4	-1	-2

a) Решите игру методами линейного программирования и определите выиг­рышные стратегии.

b) Исходя из имеющейся информации, какая из двух команд может выиг­рать чемпионат?

c) Пусть за всю игру имеется 60 возможностей владения мячом (30 владений для каждой команды). Предскажите ожидаемое количество очков, с ко­торым будет выиграна игра чемпионата.

3. Армия полковника Блотто сражается с вражеской армией за контроль над двумя стратегически важными позициями. Полковник имеет в своем распо­ряжении два полка, а его противник — три. Каждый из противников может посылать на любую позицию только целое число полков или совсем не посы­лать. Позиция будет захвачена армией, которая атакует большим количест­вом полков. Иначе результат сражения является ничейным.

a) Сформулируйте задачу в виде игры двух лиц с нулевой суммой и решите игру методами линейного программирования.

b) Какая армия выиграет сражение?

4. В игре двух лиц, именуемой двухпальцевой игрой Морра, каждый игрок по­казывает один или два пальца и одновременно отгадывает число пальцев, ко­торые покажет его противник. Игрок, который угадал, выигрывает сумму, равную суммарному числу показанных противниками пальцев. Иначе игра заканчивается вничью. Сформулируйте задачу в виде игры двух лиц с ну­левой суммой и решите игру методами линейного программирования.

5. П