LINEAR PROGRAMMING OUTPUT SUMMARY

Title: Diet Problem, Example 2.2-2
Final Iteration No.:
Objective Value =	437.65
Variable	Value	Obj Coeff	Obj Val Contrib
x1: corn	470,59	0,30	141,18
x2: soybean	329,41	0,90	296,47
Constraint	RHS	Slack-/Surplus+
1 (>)	800,00	0,00
2(<)	0,00	0,00
3(>)	0,00	10,82+
•"Sensitivity Analysis*"
Variable	Current Obj Coeff	Min Obj Coeff	Max Obj Coeff	Reduced Cost
x1: corn	0,30	-0,63	0,90	0,00
x2: soybean	0,90	0,30	infinity	0,00
Constraint	Current RHS	Min RHS	Max RHS	Dual Price
1 (>)	800,00	0,00	infinity	0,55
2(<)	0,00	-138,00	168,00	-1,18
3(>)	0,00	-infinity	10,82	0,00

Рис. 2.17. Выходной отчет программы TORA

a) Определите единичную стоимость дополнительного фунта помидоров.

b) Изменится ли оптимальное решение, если склад сможет принимать больше упаковок томатного сока? А при увеличении емкости склада для упаковок томатной пасты?

c) Найдите новое оптимальное решение, если компания уменьшит объем пе­рерабатываемых помидоров до 50 000 фунтов за смену.

3. Решите задачу "диеты" из примера 2.2.2 с помощью:

a) средства Excel Поиск решения;

b) программы LINGO;

c) программы AMPL.

2.5. ПРИМЕРЫ МОДЕЛЕЙ ЛП

В этом разделе исследовано несколько реалистических моделей ЛП, в которых определение переменных и построение целевой функции и ограничений не так однозначно, как в ранее рассмотренных моделях с двумя переменными. Исполь­зование программы TORA позволит интерпретировать результаты решения этих задач ЛП.

70 Глава 2. Введение в линейное программирование _LINEAR PROGRAMMING OUTPUT SUMMARY

Title: Problem 2, Set 2.4a Final Iteration No.: 4 Objective Value = 63000

Variable Value	Obj Coeff	Obj Val Contrib
x1: Juice 500,00 x2: Paste 6000,00	18,00 9,00	9000,00 54000,00
Constraint RHS	Slack-/Surplus+
1 (<) 60000,00 2 (<) 2000,00 3 (<) 6000,00	0,00 1500,00-0,00
	""Sensitivity Analysis*	**
Variable Current Obj Coeff	Min Obj Coeff	Max Obj Coeff	Reduced Cost
x1: Juice 18,00 x2: Paste 9,00	0,00 6,00	27,00 infinity	0,00 0,00
Constraint Current RHS	Min RHS	Max RHS	Dual Price
1 (<) 60000,00 2 (<) 2000.00 3 (<) 6000,00	48000,00 500,00 1500,00	96000,00 infinity 7500.00	0,75 0.00 3,00
Рис. 2.18. Выходной отчет программы TORA
Пример 2.5.1. Кредитная политика банка
Банк Thriftem, предоставляющий полный набор банковских услуг, находится в процессе формирования портфеля кредитов объемом 12 млн. долл. В следующей таблице представлены возможные типы банковских кредитов.
Тип кредита	Ставка процента	Вероятность безнадежных долгов
Кредиты физическим лицам Кредиты на покупку автомобилей Кредиты на покупку жилья Сельскохозяйственные Коммерческие	0,140 0,130 0,120 0,125 0,100		0,10 0,07 0,03 0,05 0,02
Безнадежные долги считаются невозвратимыми, поэтому они должны вычитаться из возможного дохода. Конкурентная борьба с другими финансовыми институтами вынуждает банк не ме­нее 40% капитала помещать в сельскохозяйственные и коммерческие кредиты. Для содействия строительной индустрии своего региона банк планирует вложить в кредиты на покупку жилья не менее 50% от общей суммы кредитов физических лиц, на покупку автомобилей и жилья. Банк также поддерживает государственную политику, указывающую, что отношение безнадежных долгов ко всей сумме кре-

дитов не должно превышать 0,04.

2.5. Примеры моделей ЛП

Математическая модель. Переменные для создаваемой модели можно определить следующим образом:

х, — кредиты физическим лицам,

х₂ — кредиты на покупку автомобилей,

х₃ — кредиты на покупку жилья,

х₄ — сельскохозяйственные кредиты,

х₅ — коммерческие кредиты.

Банк Thriftem, естественно, желает максимизировать чистую прибыль, т.е. разность между доходом от инвестируемых сумм и суммой невозвращенных кредитов. По­скольку безнадежные долги считаются невозвратимыми, они вычитаются как из инвестируемых сумм, так и из общей прибыли. Исходя из этих соображений, целе­вую функцию можно записать следующим образом.

Максимизировать z = 0,14х(0,9х,) + 0,13х(0,93х₂) + 0,12х(0,97х₃) + 0,125х(0,95х₄) + + 0,1х(0,98х₅) - ОДх, - 0,07х₂ - О.ОЗх, - 0,05х₄ - 0,02д:₅.

После приведения подобных членов получаем

максимизировать z = 0,026х, + 0,0509х₂ + 0,0864х₃ + 0,06875х₄ + 0,078х₅.

Задача имеет пять ограничений.

1. Ограничение общей суммы кредитов

х₁ + х₂ + х₃ + х₄ + дг₅ < 12.

2. Ограничение на сельскохозяйственные и коммерческие кредиты

х₄+х₅>0,4х 12

или

дг₄+х₅>4,8.

3. Ограничения кредитов на покупку жилья

х₃>0,5(х₁ + х₂ + х,)

или

0,5х, + 0,5х₂-0,5х₃ <0.

4. Ограничения на невозвращенные кредиты

0,1х, +0,07х₂ +0,03х₃ +0,05х₄ +0,02х₅ ^_{Q рд} X, + X, + х₃ + x_t + х₅

или

0,06х, + 0,03х₂ - 0,01х₈ + 0,01х₄ - 0,02х₅ < 0.

5. Условия неотрицательности

х, > 0, х₂ > 0, х₃ > 0, х₄ > 0, х₅ > 0.

Необходимо сделать еще одно "тонкое" замечание, что все кредиты выделяются примерно в одно и то же время. Это позволит игнорировать временной фактор в процессе размещения капитала в различные кредиты.

Оптимальное решение сформулированной задачи линейного программирования пока­зано на рис. 2.19.⁷ Оно рекомендует использовать только кредиты на покупку жилья и коммерческие кредиты. Среди неиспользованных типов кредитов наименее при­

Все модели, рассмотренные в этом разделе, в формате программы TORA содержатся в папке ToraFiles на прилагаемом к книге компакт-диске.

Глава 2. Введение в линейное программирование

влекательны кредиты физическим лицам и не только из-за того, что коэффициент при переменной х, в целевой функции минимальный (равен 0,026), но и потому, что приве­денная стоимость таких кредитов превышает (равна 0,0604) все остальные. Приведен­ная стоимость показывает, что "рентабельность" этой переменной должна возрасти до 0,0604, чтобы кредиты для физических лиц стали привлекательными для инвестиций.

_ LINEAR PROGRAMMING OUTPUT SUMMARY

Title: Bank Loan Model, Example 2.5-1 Final Iteration No.: 7 Objective Value = 1

Variable	Value	Obj Coeff	Obj Val Contrib
x1: personal	0.00	0,03	0,00
x2: car	0.00	0,05	0,00
x3: home	7.20	0,09	0,62
x4: farm	0.00	0,07	0,00
x5: comm'l	4.80	0,08	0,37
Constraint	RHS	Slack-/Surplus+
1 (<)	12,00	0,00
2(>)	4.80	0,00
3(<)	0.00	3,60-
4(<)	0,00	0,17-
		***Sensitivity Analysis**
Variable	Current Obj Coeff	Min Obj Coeff	Max Obj Coeff	Reduced Cost
x1: personal	0,03	-infinity	0,09	0,06
x2: car	0,05	-infinity	0,09	0,04
x3: home	0,09	0.08	infinity	0.00
x4: farm	0.07	-infinity	0,08	0.01
x5: comm'l	0.08	0,07	0,09	0.00
Constraint	Current RHS	Min RHS	Max RHS	Dual Price
1 (<)	12,00	4,80	infinity	0,09
2(>)	4.80	0,00	12,00	-0,01
3(<)	0,00	-3,60	infinity	0,00
4(<)	0,00	-0,17	infinity	0.00

Рис. 2.19. Выходной отчет программы TORA для модели кредитной политики банка

Двойственная цена первого ограничения показывает, что увеличение суммы всех кредитов на единицу (млн. долл.) приводит к увеличению чистой прибыли на 0,0864 (млн. долл.). Это эквивалентно 8,64% годовых от суммы инвестиций. По­скольку соответствующий интервал для значения правой части этого ограничения простирается от 4,8 до бесконечности, указанный процент годовых гарантирован для любой общей суммы кредитов, превышающих 12 млн. долл. Но этот процент годовых, конечно, очень мал, поскольку наименьший процент по банковским вло­жениям составляет 10% (для коммерческих кредитов). Разность в величинах этих процентов обусловливают невозвращенные кредиты, которые вычитаются и из об­щей суммы кредитов, и из чистой прибыли. В формуле целевой функции наиболь­ший коэффициент (0,0864) стоит перед переменной, соответствующей объему кре­дитов на покупку жилья. Интересно, что в данном решении ему оказалась равной

2.5. Примеры моделей ЛП

двойственная цена первого ограничения. Отсюда можно заключить, что любые но­вые вложения следует размещать в виде кредитов на покупку жилья.

Второе ограничение данной задачи указывает нижнюю границу суммы сельскохозяй­ственных и коммерческих кредитов. Отрицательная двойственная цена (-0,0084) пока­зывает, что увеличение этой границы приведет к уменьшению чистой прибыли банка. Другими словами, экономически не выгодно устанавливать нижнюю границу для суммы сельскохозяйственных и коммерческих кредитов. Это еще раз подтверждает, как было видно при рассмотрении первого ограничения, что любые дополнительные вложения следует помещать в кредиты на покупку жилья, а не в сельскохозяйствен­ные и коммерческие кредиты. Если мы вообще удалим это ограничение, все инвести­ции переместятся в кредиты на покупку жилья. Проверьте это утверждение, удалив второе ограничение и решив новую задачу с помощью программы TORA (для этого дос­таточно использовать опцию MODIFY (Изменить) при решении текущей задачи).

Пример 2.5.2. Освоение и использование земли

Компания Birdeyes владеет 800 акрами необработанной земли с живописным озером в центре горного массива Озарк. В прошлом освоение территории вокруг озера про­исходило нерегулярно и понемногу. Сейчас вокруг озера построено много домиков для отдыхающих. Поскольку канализация отсутствует, интенсивно используются септические контейнеры (большие емкости для хранения бытовых отходов). В на­стоящее время многие контейнеры приходят в негодность (текут), поэтому появи­лись проблемы с загрязнением воды в озере.

Чтобы предотвратить дальнейшее загрязнение озера, официальные власти округа разработали строгие ограничительные требования для возможного дальнейшего освоения этой территории.

1. Разрешается возводить домики только на одну, две или три семьи, причем доля домиков на одну семью должна составлять не менее 50% от всех построенных.

2. Ограничивается количество септических контейнеров: минимальная террито­рия, отведенная для размещения одного контейнера, обслуживающего один до­мик на одну, две или три семьи, составляет соответственно 2, 3 и 4 акра.

3. Рекреационная зона рассчитывается исходя из нормы — не менее одного акра на 200 семей.

4. Для предотвращения загрязнения озера запрещается использовать поверхност­ные воды для полива и бытовых нужд.

Правление компании Birdeyes решило изучить возможности дальнейшего освоения тех 800 акров земли, которые ей принадлежат. Дальнейшее освоение этих земель предусматривает строительство домиков для отдыха на одну, две и три семьи. Под­считано, что необходимо отвести не менее 15% всей территории на прокладку дорог и строительство вспомогательных сооружений. Компания планирует сдавать домики отдыхающим и рассчитывает получить от одного домика следующую прибыль.

Тип домика	на одну семью	на две семьи	на три семьи
Чистая прибыль (долл.)	10 000	12 000	15 000

Стоимость планируемой водопроводной сети пропорциональна количеству доми­ков, подключенных к водопроводу. Однако власти округа настаивают на том, что

Глава 2. Введение в линейное программирование

необходимо собрать не менее 100 ООО долл., чтобы этот проект был экономически осуществимым. Кроме того, известно, что даже в пиковый период водопроводная сеть не сможет поставить больше 200 ООО галлонов воды в день. В следующей таб­лице приведена стоимость подключения к водопроводной сети одного домика и указана ежедневная потребность в воде одной средней семьи.

Тип домика	на одну	на две	натри	Рекреационная
	семью	семьи	семьи	зона
Стоимость подключения к водопроводу (долл.)
Потребность в воде (галлон/день)

Математическая модель. Компания должна определить, сколько строить домиков различного типа и какова должна быть рекреационная зона, чтобы удовлетворить требованиям властей округа. Пусть

jCj — количество домиков на одну семью,

х_г — количество домиков на две семьи,

х₃ — количество домиков на три семьи,

х₄ — количество акров земли, отводимых под рекреационную зону.

Очевидно, что компания должна максимизировать свой доход, поэтому целевую функцию можно записать так:

максимизировать z = ЮООх, + 12000д:₂ + 15000;с₃.

Задача имеет следующие ограничения.

1. Ограничение на общую площадь используемой земли.

2. Ограничение, связанное со строительством домиков преимущественно на одну семью.

3. Ограничение, учитывающее требования к рекреационной зоне.

4. Ограничение, связанное со строительством водопроводной сети.

5. Ограничение на потребление воды в пиковый период.

Эти ограничения математически будут записаны следующим образом.

1. Ограничение на общую площадь используемой земли:

2дг, + Зх_г + 4х₃ + lx_t < 680 (= 0,85 х 800).

2. Ограничение, связанное со строительством домиков преимущественно на одну семью:

-3->0,5

Х + х_г + х₃

или

0,5дг,-0,5д:₂-0,5д:₃>0.

3. Ограничение, учитывающее требования к рекреационной зоне:

_ х, + 2х, + Зх,

х.>—---

или

200л:,-л:, - 2x₂-3x_a>0.

2.5. Примеры моделей ЛП

4. Ограничение, связанное со строительством водопроводной сети:

1000л:, + 1200л:₂ + 1400д-₃ + ⁸⁰⁰*4 * ^{100 00}°-

5. Ограничение на потребление воды в пиковый период:

400л:, + 600лг₂ + 840*₃ + 450*₄ < 200 ООО.

6. Условия неотрицательности:

*,>0,*₂>0,*₃>0,*₄>0.

Еще на этапе формулирования математической модели следует обращать внимание на возможные проблемы, которые могут возникнуть из-за ошибок машинного округ­ления. В нашей модели коэффициенты в четвертом и пятом ограничениях значи­тельно больше по величине, чем все остальные. Эта несоразмерность (относительная) величин коэффициентов может привести к непредвиденным ошибкам машинного округления и, следовательно, к неверному результату. В нашем случае мы можем предотвратить эту потенциальную опасность путем масштабирования коэффициен­тов, для чего все коэффициенты в четвертом и пятом неравенствах надо разделить на 1000. После этого неравенства будут записаны следующим образом.

*, + 1,2*₂ + 1,4*₃ + 0,8*₄ > 100,

0,4*i + °>⁶*₂ + 0,84*з + °.45*₄ < 200.

К подобным вычислительным проблемам может привести и наличие в неравенст­вах слишком малых по величине коэффициентов. В этом случае также применяет­ся масштабирование коэффициентов, но уже в сторону их увеличения. Большинст­во программного обеспечения, предназначенного для решения задач ЛП (включая программу TORA), пытается согласовать величины коэффициентов еще до начала расчетов. Однако это желательно сделать еще на этапе формализации модели.

На рис. 2.20 представлено оптимальное решение для построенной модели. Отметим, что обычная задача линейного программирования не предполагает целочисленного решения. Поэтому мы получили значения *, = 339,15, *₄ = 1,70 и *₂ = *₃ = 0. Мы мо­жем округлить полученные значения, тогда *, = 339 и *₄ = 2 (эти значения в данном случае совпадут с оптимальным решением задачи целочисленного линейного про­граммирования).

Оптимальное решение не рекомендует строить домики на две и три семьи, несмотря на то что доходность этих домиков (12 000 и 15 000 долл.) выше, чем домиков, рас­считанных на одну семью. Этот результат показывает, что только по коэффициен­там целевой функции нельзя судить о "рентабельности" отдельных видов эконо­мической деятельности, которым соответствуют данные коэффициенты. Следует учитывать также стоимость ресурсов, необходимых для осуществления такой деятельности. Это тот фактор, который выражается приведенной стоимостью. Приведенные стоимости для домиков на две и три семьи составляют 3012,47 и 5024,94 долл. соответственно. Это означает, что для того, чтобы такие домики были рентабельными, необходимо либо на величины приведенных стоимостей уменьшить стоимость ресурсов, необходимых для их строительства и эксплуата­ции, либо на такую же величину увеличить их доходность.

В ограничениях 2, 4 и 5 дополнительные переменные имеют положительные значения, а это указывает на то, что соответствующие "ресурсы" использованы не полностью. В результате двойственные цены, соответствующие этим ограничениям, равны нулю. Двойственная цена первого ограничения (ограничение на общую площадь используе­

Глава 2. Введение в линейное программирование

мой земли) равна 4987,53 долл.; это говорит о том, что увеличение общей площади на один акр должно принести 4987,53 долл. чистой прибыли. Эту информацию можно ис­пользовать для определения цены при покупке дополнительного земельного участка.

_LINEAR PROGRAMMING OUTPUT SUMMARY___

Title: Land Use Model, Example 2.5-2 Final Iteration No.: 8 Objective Value = 3391521.2

Variable	Value	Obj Coeff	Obj Val Contrib
x1: single	339,15	10000,00	3391521,20
x2: double	0,00	12000.00	0,00
x3: triple	0,00	15000,00	0,00
x4: recr'n	1,70	0,00	0,00
Constraint	RHS	Slack-/Surplus+
1 (<)	680,00	0,00
2(>)	0,00	169,58+
3(>)	0,00	0,00
4(>)	100,00	240,51 +
5(<)	200,00	63,58-
•"Sensitivity Analysis***
Variable	Current Obj Coeff	Min Obj Coeff	Max Obj Coeff	Reduced Cost
x1: single	10000,00	7993,36	infinity	0,00
x2: double	12000,00	-infinity	15012,47	3012,47
x3: triple	15000,00	-infinity	20024,94	5024,94
x4: recr'n	0,00	-infinity	5000,00	0,00
Constraint	Current RHS	Min RHS	Max RHS	Dual Price
1 (<)	680,00	199,70	996,89	4987,53
2(>)	0,00	-infinity	169,58	0,00
3(>)	0,00	-340,00	50988,00	-24,94
4(>)	100,00	-infinity	340,51	0,00
5(<)	200.00	136,42	infinity	0,00

Рис. 2.20. Выходной отчет программы TORA для модели использования земли

В третьем ограничении двойственная цена равна -24,94 долл. (если точно, то -4,9377 долл.), поэтому любое увеличение этого "ресурса" приведет к снижению общего дохода. Но почему так происходит? Чтобы ответить на этот вопрос, нужно знать, сколько единиц этого "ресурса" содержится в данном ограничении. Рас­смотрим это ограничение подробнее.

200л"₄-л-, - 2х₂- Зл-₃ >0.

Неравенство показывает, что минимальная площадь рекреационной зоны зависит от количества домиков. В такой записи единицы измерения левой части неравенст­ва не видны. Поэтому мы разделим все неравенство на 200, в результате получим

х₄ - (0,005л-, + 0,01л:₂ + 0,015л-₃) > 0.

Поскольку площадь рекреационной зоны измеряется в акрах, выражение в скобках также должно измеряться в акрах. Поэтому увеличение на одну единицу правой части

2.5. Примеры моделей ЛП

неравенства (т.е. возрастание от 0 до 1) можно интерпретировать как увеличение на один акр площади рекреационной зоны. На основании такого представления ограни­чения можно сказать, что двойственная цена соответствует стоимости увеличения на акр рекреационной зоны. Но новая запись ограничения показывает, что двойствен­ная цена должна быть равной 200 х (-24,9377) = -4987,54 долл. (Повторив расчеты программы TORA при такой записи третьего ограничения, вы должны получить именно такую величину двойственной цены — проверьте это!)

Новая двойственная цена свидетельствует о том, что увеличение площади рекреа­ционной зоны на один акр приведет к уменьшению общего дохода на 4987,54 долл. Интересно, что это число в точности равно двойственной цене первого ограничения, но с противоположным знаком. Такой результат имеет экономический смысл, по­скольку перевод акра земли в рекреационную зону означает исключение этого акра земли из той площади, на которой можно построить домики, приносящие прибыль. Поэтому не стоит удивляться, что эти величины совпадают.

Пример 2.5.3. Расписание движения автобусов

Городская транспортная компания изучает возможность ввести такую систему дви­жения городских автобусов, которая снизила бы проблему загазованности в городе путем уменьшения количества используемых автобусов. Вначале нужно было опре­делить минимальное количество автобусов, необходимое для удовлетворения транс­портных потребностей горожан. Оказалось, что в различное время суток требуется разное количество автобусов. Дальнейшее изучение этого вопроса позволило аппрокси­мировать суточную потребность в автобусах кусочно-постоянной функцией с 4-часовыми интервалами постоянных значений. Эта функция показана на рис. 2.21. При составле­нии расписания движения автобусов следует учитывать, что каждый автобус должен находиться на линии непрерывно в течение 8 часов (одна рабочая смена).

Математическая модель. Итак, требуется определить число автобусов, выходящих на линию в определенную смену (т.е. переменные), так, чтобы удовлетворить ми­нимальные потребности в транспортных услугах (ограничения) и по возможности минимизировать общее количество автобусов, выходящих на линию в течение су­ток (целевая функция).

Нетрудно заметить, что такое определение переменных неоднозначно. Мы знаем, что каждый автобус должен отработать 8-часовую смену, но мы не знаем, когда эта смена должна начинаться. Если следовать схеме обычной 3-сменной работы (1-я смена с8:01 до 16:00, 2-я — с 16:01 до 24:00 и 3-я — с 00:01 до 8:00) и обозначить через х₂ и.г₃ количество автобусов, работающих на линии в эти смены, тогда, исходя из транс­портных потребностей (рис. 2.21), получаем х, > 10, х₂ > 12 их₃ > 8, а общее количество ежедневно используемых автобусов составляетх_х +х₂ + х_ъ = 10 + 12 + 8 = 30. Это решение приемлемо, если смены должны начинаться так, как при обычной ор­ганизации 3-сменной работы. Однако можно оптимизировать расписание движе­ния автобусов, если поискать другое, "лучшее" время начала рабочих смен. Пред­положим, что между началом "соседних" смен может быть 4 часа, а не 8, как в обычной схеме 3-сменной работы. В нижней части рис. 2.21 показана такая схема организации перекрывающихся рабочих смен, согласно которой они должны на­чинаться в 00:01, 4:01, 8:01, 12:01, 16:01 и 20:01, при этом каждая смена продол­жается 8 часов. Теперь мы готовы определить переменные:

Глава 2. Введение в линейное программирование

24:00

4:00

8:00

12:00

16:00

20:00

24:00

•-н

•-н

^ХЪ

•-н

•-н

^xs

Рис. 2.2/. График суточной потребности в автобусах

x_t — количество автобусов, начинающих работу в 00:01,

х₂ — количество автобусов, начинающих работу в 4:01,

х₃ — количество автобусов, начинающих работу в 8:01,

x_t — количество автобусов, начинающих работу в 12:01,

х₆ — количество автобусов, начинающих работу в 16:01,

х₆ — количество автобусов, начинающих работу в 20:01.

Задача линейного программирования будет записана следующим образом.

Минимизировать z = х, + х₂ + х_г + x_t + х_ъ + x_t при выполнении условий

x_t + x_t > 4 (время от 00:01 до 4:00), х_х + х₂ > 8 (время от 4:01 до 8:00), х₂+х_г> 10(время от 8:01 до 12:00), х₃ + x_t > 7 (время от 12:01 до 16:00), x_t +х_й > 12 (время от 16:01 до 20:00), x_s + х₆ > 4 (время от 20:01 до 24:00),

x_y^o,;-i,2,...,e.

2.5. Примеры моделей ЛП

Результаты решения этой задачи ЛП представлены на рис. 2.22. Отметим, что в оптимальном решении общее количество автобусов равно 26, при этом *, = 4, х₂ = 10, х_г = 0, x_t = 8, х_ъ = 4 и х₆ = 0. Приведенные стоимости всех переменных равны нулю; это указывает на альтернативные оптимальные решения (но с тем же значе­нием целевой функции).

Интерес представляет информация о рассчитанных двойственных ценах. Двойст­венная цена, равная 1, показывает, что увеличение правой части соответствующего неравенства на единицу увеличивает общее количество автобусов также на едини­цу. Если двойственная цена равна нулю, то увеличение значения правой части со­ответствующего неравенства не приводит к возрастанию общего числа используе­мых автобусов. Однако эти утверждения справедливы только тогда, когда значения правых частей неравенств не выходят за пределы соответствующих интервалов (значения в столбцах Min RHS и Max RHS последней таблицы отчета на рис. 2.22).

__LINEAR PROGRAMMING OUTPUT SUMMARY_

Title: Bus Sceduling Model, Example 2.5-3 Final Iteration No.: 10 Objective Value = 26

Variable	Value	Obj Coeff	Obj Val Contrib
x1:12:01AM	4,00	1,00	4,00
x2: 4:01AM	10,00	1,00	10,00
x3: 8:01AM	0,00	1,00	0,00
x4: 12:01PM	8,00	1,00	8,00
x5: 4:01PM	4,00	1,00	4,00
x6: 8:01PM	0,00	1,00	0,00
Constraint	RHS	Slack-/Surplus+
1(>)	4,00	0,00
2(>)	8,00	6,00+
3(>)	10.00	0,00
4(>)	7,00	1,00+
5(>)	12,00	0,00
6(>)	4,00	0,00
		'"Sensitivity Analysis'
Variable	Current Obj Coeff	Min Obj Coeff	Max Obj Coeff	Reduced Cost
x1: 12:01AM	1,00	0,00	1,00	0,00
x2: 4:01AM	1,00	0,00	1,00	0,00
x3: 8:01AM	1,00	1,00	infinity	0,00
x4:12:01PM	1,00	1,00	1,00	0,00
x5: 4:01PM	1,00	1,00	1,00	0,00
x6: 8:01PM	1,00	1,00	infinity	0,00
Constraint	Current RHS	Min RHS	Max RHS	Dual Price
K>)	4,00	0,00	infinity	1,00
2(>)	8,00	-infinity	14,00	0,00
3(>)	10,00	4,00	infinity	1,00
4(>)	7,00	-infinity	8,00	0,00
5(>)	12,00	11,00	infinity	1,00
6(>)	4,00	0,00	5,00	0,00

Рис. 2.22. Выходной отчет программы TORA для задачи составления расписания движения автобусов

Глава 2. Введение в линейное программирование

Например, правая часть второго неравенства может возрасти от 8 до 14 без увели­чения общего количества используемых автобусов. А увеличение на какое-либо значение правой части третьего неравенства (начиная со значения 10 и выше) при­водит к такому же увеличению общего количества автобусов. Эта информация очень важна для анализа оптимального решения.

Анализ чувствительности коэффициентов целевой функции в данном случае не имеет особого смысла, поскольку в этой модели они могут иметь только значение 1. Если бы целевая функция отражала какую-нибудь другую "цель" (например, ми­нимизировала бы стоимость эксплуатации автобусов), тогда ситуация могла быть иной и анализ этих коэффициентов имел бы смысл.

Пример 2.5.4. Минимизация потерь при разрезании рулонов бумаги

Тихоокеанская бумажная фабрика производит стандартные рулоны бумаги шири­ной в 20 футов. Специальные заказы клиентов требуют разрезания стандартных рулонов. Типовой заказ (такие заказы могут меняться каждый день) приведен в следующей таблице.

Позиции заказа	Требуемая ширина рулона (футы)	Требуемое количество рулонов (шт.)

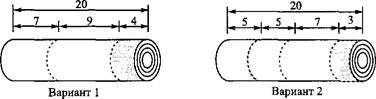
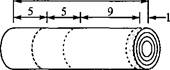
На фабрике заказы выполняются путем разрезания специальными ножами стан­дартных рулонов на требуемые. Существует несколько вариантов деления стан­дартного рулона, три из которых показаны на рис. 2.23. Конечно, существуют и другие варианты, не показанные на этом рисунке (они будут описаны ниже), но сейчас мы ограничимся только представленными. Для выполнения заказа можно совместно использовать несколько вариантов разрезки стандартных рулонов. На­пример, для выполнения заказа, приведенного в таблице, можно применить сле­дующие комбинации вариантов 1, 2 и 3.

1. Разрезать 300 стандартных рулонов, используя вариант 1, и 75 рулонов с помо­щью варианта 2.

2. Разрезать 200 стандартных рулонов, используя вариант 1, и 100 рулонов с по­мощью варианта 3.

Какая из этих комбинаций лучше? Чтобы ответить на этот вопрос, надо рассмот­реть потери от каждой из них. На рис. 2.23 серым цветом показаны отходы бумаги после каждого варианта разрезки. Мы можем оценить преимущества каждой ком­бинации, если подсчитаем суммарные отходы, полученные после их применения. Но, поскольку отрезки рулонов, идущие в отходы, имеют разную длину, нам надо подсчитать объем этих отходов, а не просто количество отрезков. Предполагая, что стандартный рулон бумаги имеет площадь поперечного сечения, равную L квадрат­ным футам, подсчитываем потери для комбинаций 1 и 2.

Комбинация 1: 300х(4 xL) + 75х(3 xL) = 1425L куб. футов.

Комбинация 2: 200х(4 xL) + 100х(1 xL) = 900L куб. футов.

2.5. Примеры моделей ЛП

Вариант 3

Рис. 2.23. Варианты разрезки стандартных рулонов (размеры да­ны в футах )

Если число рулонов шириной 5, 7 или 9 футов, которые были получены в результате применения какой-либо комбинации вариантов разрезки, превышает количество, необходимое для выполнения заказа, то разность между ними также следует отнести к потерям. В первой комбинации при использовании варианта 1 получено 300 -- 200 = 100 лишних рулонов шириной 7 футов; применение варианта 2 добавляет еще 75 лишних рулонов такой же ширины. Таким образом, дополнительные потери со­ставляют 175x(7xL)= 1225L куб. футов. Комбинация 2 не производит лишних рулонов шириной 7 и 9 футов, но применение варианта 3 приводит к появлению 200 - 150 = 50 лишних рулонов шириной 5 футов, что составляет 50 х (5 х L) = 250L куб. футов дополнительных отходов бумаги. В результате этих выкладок имеем следующее.

Объем отходов от комбинации 1 = 1425L + 1225L = 2650L куб. футов.

Объем отходов от комбинации 2 = 900L + 250L = 1150L куб. футов.

Очевидно, что комбинация 2 лучше, так как имеет меньше отходов.

Для получения оптимального решения данной задачи необходимо определить все до­пустимые варианты разрезки стандартных рулонов и затем получить все возможные комбинации этих вариантов. Хотя определить все допустимые варианты разрезки не­сложно, перебор всех комбинаций этих вариантов уже является нетривиальной зада­чей. Здесь необходим систематический подход к организации такого перебора. В дан­ном случае это поможет выполнить модель линейного программирования.

Математическая модель. Мы должны найти комбинацию вариантов разрезки (переменные), с помощью которой можно было бы. выполнить заказ (ограничения) с минимальными отходами бумаги (целевая функция).

Переменные надо определить таким образом, чтобы их значения можно было ин­терпретировать в способ разрезки стандартных рулонов бумаги. Поэтому опреде­лим переменные как количество стандартных рулонов, разрезанных с помощью конкретных вариантов. Это определение требует описать все возможные вариан­ты разрезки. Три варианта показаны на рис. 2.23, остальные приведены в следую­щей таблице. Убедитесь, что не пропущены еще какие-нибудь варианты разрезки, при этом помните, что в допустимом варианте разрезки ширина остатка стандарт­ного рулона должна быть меньше 5 футов.

Глава 2. Введение в линейное программирование

Требуемая ширина			Варианты			Требуемое количество
(футы)							рулонов
Остаток (футы)

Теперь можно определить переменные: л — количество стандартных рулонов, раз­резанных вариантомj,j = 1, 2, 6.

Ограничение в этой модели заключается в том, что произведенных рулонов задан­ных размеров (5, 7 и 9 футов) должно быть достаточно для выполнения заказа. Ес­ли использовать все варианты разрезки, приведенные в таблице, то получим, что

количество рулонов шириной 5 футов = 2х₂ + 2х₃ + Ax_t + х_а,

количество рулонов шириной 7 футов = дг, + дг₂ + 2х_ъ,

количество рулонов шириной 9 футов = дг, + дг₃ + 2х₆.

Эти числа должны быть не меньше 150, 200 и 300 соответственно.

Для построения целевой функции заметим, что общий объем отходов можно под­считать как разность между объемом всех использованных стандартных рулонов и объемом рулонов, необходимых для выполнения заказа. Запишем это следую­щим образом:

объем использованных стандартных рулонов = 20Цдг, + х₂ + х₃ + дг₄ + х_ъ + х₆),

объем заказных рулонов = Ц150 х 5 + 200 х 7 + 300 х 9) = 4750/_.

Поскольку объем рулонов, необходимых для выполнения заказа, постоянен, а также постоянна величина поперечного сечения L, целевую функцию можно за­писать просто как сумму всех переменных: г = дг, + х₂ + х₃ + дг₄ + х_ъ + дг₆.

Таким образом, получаем следующую задачу линейного программирования. Минимизировать z = дг, + х₂ + х₃ + x_t + дг₅ + х₆

при выполнении условий

2дг₂ + 2дг₃ + 4x_t + дг₅ > 150 (ограничение на рулоны шириной 5 футов), дг, + дг₂ + 2дг₅ > 200 (ограничение на рулоны шириной 7 футов), дг, + дг₃ + 2дг₆ > 300 (ограничение на рулоны шириной 9 футов), x>0,j=l,2, ...,6.

Оптимальное решение этой задачи, представленное на рис. 2.24, показывает, что задача имеет и другие оптимальные решения, где для выполнения того же заказа используется такое же количество рулонов стандартной длины, но применяются другие варианты разрезки. В приведенном решении 12,5 стандартных рулонов раз­резаются в соответствии с вариантом 4, 100 стандартных рулонов — в соответствии с вариантом 5, а 150 стандартных рулонов— с вариантом 6. В таком виде это ре­шение нельзя реализовать, так как значение переменной дг, нецелое. В этой ситуа­ции можно применить к данной задаче алгоритм целочисленного программирова­ния (см. главу 9) или округлить значение переменной дг₄ до 13.

2.5. Примеры моделей ЛП