Silver-Meal Heuristic Inventory Model

Input data:

i Number of periods, N =		: .^Maximum 14 periods
Period t=
Setup cost, Kt =
Holding cost. ht =
Demand, Dt =
Solution complete	Model calculations:			Optimum solution (Total cost"	$122 00)-
1 Start Iteration at Period	Period		TC
				0 00	20 00
				1.00	35 00
				2 00	49.00
				3 00	109.00
				6 00|	187.00
	в			7 00	362.00		Order 32 m period 1 for periods 1 to 3, cost - S49.00
			20 0.00	18.00
				3.00	57.00
	6 1			4.00*	157.00		Order 20 in period 4 for periods 4 to 4, cost - $18.00
S			13 0.00	~ 5.00		_
			38 1.00	30.00		Ordsr 13 in period 5 for periods 5 to 5, cost - SS.00
						__	____L_	i
e				0.00	50.00		Ordsr 25 in peiiod 61or periods 6to 6, cost - S50.00

Рис. 11.12. Решение в Excel задачи из примера 11.3.4

Глава 11. Детерминированные модели управления запасами

с четвертого периода. Поэтому, пропустив пустую строку от ранее вычисленных значений, вводим значение 4 в ячейку F18. Это действие инициирует вычисления второй итерации, откуда находим, что локальному минимуму функции TCU соот­ветствует t = 4 (четвертый период) со значением TCU = 18,00. Поэтому третья ите­рация должна начаться с пятого периода, для чего в ячейку F22 вводим значение 5. На третьей итерации локальному минимуму функции TCU соответствует t = 5 (пятый период). Следовательно, для начала последней итерации надо ввести чис­ло 6 в ячейку F25. При выполнении каждой итерации рабочий лист автоматически отображает оптимальное решение, соответствующее этой итерации, и величину общих затрат, как показано на рис. 11.12 в столбце М.

УПРАЖНЕНИЯ 11.3.5

1. Спрос на удилища достигает своего минимума в декабре, а максимума — в ап­реле. Компания, которая изготовляет удилища, оценивает декабрьский спрос на них в 50 единиц. Затем спрос увеличивается на 10 удилищ в месяц, достигая максимального значения 90 единиц в апреле. После этого объем спроса умень­шается на 5 удилищ в месяц. Стоимость размещения заказа на изготовление партии удилищ равна 250 долл. на протяжении всех месяцев, за исключени­ем февраля, марта и апреля, когда она составляет 300 долл. Стоимость про­изводства одного удилища является примерно постоянной на протяжении всего года и составляет 15 долл., а стоимость хранения одного удилища равна 1 долл. в месяц. Требуется составить план производства удилищ.

2. На протяжении последующих 12 месяцев небольшое издательство переиздает роман в целях удовлетворения спроса на него: 100, 120, 50, 70, 90, 105, 115, 95, 80, 85, 100 и 110 экземпляров. Стоимость размещения заказа на переизда­ние равна 200 долл., а стоимость хранения книги на протяжении одного ме­сяца — 1,20 долл. Определите план переиздания книги издательством.

ЛИТЕРАТУРА

1. Silver Е., Руке D. and Peterson R. Inventory Management and Production Plan­ning and Scheduling, 3rd ed., Wiley, New York, 1998.

2. Tersine R. Principles of Inventory and Materials Management, 3rd ed., North Holland, New York, 1988.

3. Waters C. Inventory Control and Management, Wiley, New York, 1992.

Литература, добавленная при переводе

1. Кофман А. Методы и модели исследования операций. — М.: Мир, 1966.

2. Мур Дж., Уэдерфорд Л. Экономическое моделирование в Microsoft Excel. — М.: Издательский дом "Вильяме", 2004.

КОМПЛЕКСНЫЕ ЗАДАЧИ

11.1. Распределительный центр универмага специализируется на ежедневной покупке и хранении предметов торговли, вышедших из моды. Постоянный спрос на такие предметы поступает от многочисленных торговых точек

Комплексные задачи

универмага. В прошлом решения относительно того, когда и сколько товара заказывать, перекладывались на отдел поставки, главная задача которого состояла в том, чтобы приобрести продукцию в достаточно больших объе­мах, дабы гарантировать низкие закупочные цены. Эта стратегия применя­лась без надлежащего рассмотрения фактора хранения продукции. Дейст­вительно, решения относительно того, сколько товара закупать, основывались на годовой стоимости спроса на товар на уровне распредели­тельного центра. Например, если единица продукции приобретается по цене 25 долл. и в год используется 10 ООО единиц, то годовая стоимость спроса на этот товар составляет 250 ООО долл. Отдел поставки руководствовался основ­ным принципом: чем выше годовая стоимость спроса на товар, тем больше его следует запасать в распределительном центре. Этот принцип затем выражал­ся в объеме запаса продукции, который должен храниться в распределитель­ном центре в период между пополнениями. Например, отдел поставки мог за­купать заранее определенное количество продукции каждые три месяца.

Чтобы улучшить стратегию управления запасами, руководство универмага ре­шило прибегнуть к услугам консультанта по исследованию операций. Изучив ситуацию, он пришел к выводу, что интенсивность потребления большинства видов продукции в распределительном центре с практической точки зрения яв­ляется постоянной и что проводится политика отсутствия дефицита. Дальней­шее изучение показало, что стоимость хранения всех рассматриваемых видов продукции составляет один и тот же постоянный процент от закупочной цены. Кроме того, стоимость размещения заказа для всех рассматриваемых видов продукции является одинаковой. С помощью этой информации консультант смог построить для каждого вида продукции соответствующую кривую, ко­торая устанавливает связь годовой стоимости спроса на товар со средним вре­менем между пополнениями товара. Эта кривая была затем использована для того, чтобы выяснить, какой продукции в настоящее время имеется излиш­ний запас, а какой — недостаточный. Как консультант сделал это?

11.2. Компания производит конечный продукт с использованием единственного комплектующего блока, который она закупает у внешнего поставщика. Спрос на конечный продукт является постоянным и равен примерно 20 из­делиям в неделю. Для изготовления каждой единицы конечного продукта требуется два комплектующих блока. Имеется также следующая информа­ция для рассматриваемой задачи управления запасами.

	Комплектующие	Продукция
Стоимость размещения заказа (долл.)
Стоимость хранения единицы в неделю (долл.)
Срок изготовления (недели)

Неудовлетворенный спрос на готовую продукцию является задолженностью компании и приносит ей потери в 8 долл. в неделю за единицу спроса. Раз­работайте стратегию как размещения заказов на комплектующие, так и производства конечной продукции.

11.3. Компания производит сезонную продукцию, спрос на которую ощутимо ме­няется от месяца к месяцу. Данные об объемах спроса (в количестве единиц продукции) за последние пять лет приведены в следующей таблице.

Глава 11. Детерминированные модели управления запасами

 

Месяц			Год
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь

Принимая во внимание колебания спроса на продукцию, менеджер по управлению запасами избрал стратегию, в соответствии с которой заказы на продукцию размещаются поквартально: 1 января, 1 апреля, 1 июля и 1 октября. При этом объем заказа покрывает объем спроса соответствую­щего квартала. Срок между размещением заказа и его получением равен 3 месяца. Оценки объема спроса на текущий год принимаются равными со­ответствующим показателям пятого года плюс дополнительно 10 % в каче­стве безопасности.

Новый сотрудник верит в то, что можно достичь более эффективной страте­гии управления запасами, используя экономичный объем заказа, основан­ный на среднемесячном объеме спроса на продукцию за год. Колебания спроса могут быть сглажены путем размещения заказов, которые по объему примерно равны экономичному объему партии и покрывают спрос несколь­ких последовательных месяцев. В отличие от менеджера, новый сотрудник считает, что оценки объема спроса на следующий год должны основываться на усредненных показателях для четвертого и пятого годов.

Во всех вычислениях, связанных с хранением продукции, компания счита­ет, что затраты на хранение единицы продукции на протяжении месяца равны 0,50 долл. Стоимость размещения нового заказа равна 55 долл.

Предложите стратегию управления запасами для компании.

ГЛАВА 12

ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Все методы решения задач исследования операций, изложенные в предыдущих главах, предполагают, что необходимые для их реализации данные известны точно. Однако это предположение выполняется не во всех случаях. Например, потреб­ность в электроэнергии в летние месяцы может меняться от года к году в зависимости от погодных условий. В таких случаях представление потребности в виде постоян­ной детерминированной величины неприемлемо. Вместо этого можно использовать данные наблюдений или статистические источники для описания потребности с помощью вероятностного распределения.

12.1. ЗАКОНЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Понятие вероятности ассоциируется с проведением эксперимента, результаты которого, именуемые исходами, изменяются случайным образом. Множество всех возможных исходов эксперимента называется пространством событий, а любое подмножество этого пространства — событием. Например, в эксперименте с броса­нием игральной шестигранной кости исход соответствует грани кости, т.е. может принимать значение от 1 до 6. Следовательно, пространство событий представляет собой множество {1, 2, 3, 4, 5, 6}. Примером события в этом эксперименте может, например, быть выпадение четного числа (2, 4 или 6).

Эксперимент может быть связан также с непрерывным пространством событий. Например, время между отказами некоторого электронного устройства может при­нимать любое неотрицательное значение.

Если в эксперименте, состоящем из п опытов, событие Е имеет место т раз, то вероятность Р{Е) появления события Е математически определяется соотношением

Р{Е] = im—.

Приведенное определение означает, что если эксперимент повторяется бесконечное число раз (п -» оо), искомая вероятность представляется граничным значением дро­би т/п. Это определение можно проверить, проведя эксперимент с бросанием моне­ты, исходами которого являются выпадение герба (Г) и решетки (Р). Чем большее число раз бросается монета (проводится эксперимент), тем ближе оценки Р{Р} и Р{Г} к теоретическому значению 0,5.

Глава 12. Основы теории вероятностей

По определению

0<Р{Е}< 1,

где вероятность Р{Е} равна 0, если событие Е невозможно, и 1, если оно досто­верно. Например, в эксперименте с шестигранной игральной костью выпадение семерки является невозможным событием, тогда как любое целое число от 1 до 6 — событие достоверное.

1. В ходе анализа, проведенного в средних школах штата Арканзас в целях изучения зависимости между успеваемостью по математике и поступлением в технические колледжи, получены следующие данные: из 1000 опрошенных выпускников 400 изучали математику. Из тех, кто изучал математику, лишь 150 были приняты в технические колледжи.

a) Определите вероятность того, что студент, изучавший математику, 1) по­ступит в технический колледж, 2) не поступит в технический колледж.

b) Определите вероятность того, что студент, не изучавший математику, не поступит в технический колледж.

2. Рассмотрим случайную совокупность из п человек. Определите наименьшее п такое, что более вероятным будет событие, состоящее в совпадении дней рождения нескольких человек (т.е. более вероятным по сравнению с событи­ем, что у всех индивидуумов в данной совокупности даты рождения различ­ны). (Совет. Предположите, что нет високосных годов и все дни года с равной вероятностью могут быть днем рождения каждого человека.)

12.1.1. Закон сложения вероятностей

Для данных двух событий Е и F запись Е + F обозначает их объединение, a EF — пересечение. События Е и F называются несовместными (взаимно исклю­чающими), если они не пересекаются, т.е. наступление одного события исключает возможность реализации другого. При принятых определениях закон сложения вероятностей определяется соотношением

Вероятность того, что события Е и F произойдут одновременно, обозначается как P{EF}. Если эти события независимы, тогда

P{EF)=P{E)P{F}.

Пример 12.1.1

Рассмотрим эксперимент с игральной костью. В данном случае пространство собы­тий представляет собой множество {1, 2, 3, 4, 5, 6}. Для симметричной кости имеем

УПРАЖНЕНИЯ 12.1.1

Р{Е} + P{F}, если Е и F несовместные,

Р{Е}+ P{F)- P{EF) в противном случае.

Р{1}=Р{2} = Я{3} = Я{4} = Р{5} = Я{6} = 1.

Определим события

£ = {1,2, 3 или 4}, F = {3,4 или 5}.

12.1. Законы теории вероятностей 509

Исходы 3 и 4 являются общими для событий Е и F. Следовательно, EF = = {3 или 4}. Имеем

/»{£} = Р{1} ₊ Р{2} + /'{3} _{+ /}'{4} = 1 ₊ 1 ₊ 1 ₊ 1 = |.

P{F} = P{3} ₊ P{4} ₊ P{5} = i ₊ I ₊ I = i

P{EF} = P{3} ₊ P{A} = y_r¹-. Отсюда следует, что

Р{Е + F} = Р{Е} + P{F} - P{EF) = I + 1 - I = |.

Чисто интуитивно этот результат понятен, так как событие (£ + F) = {1, 2, 3, 4, 5}, очевидно, имеет вероятность 5/6.

УПРАЖНЕНИЯ 12.1.2

1. Игральная кость бросается дважды. Обозначив через Е и F исходы независи­мых бросаний, вычислите вероятности следующих событий.

a) Сумма £ и F равна 11.

b) СуммаЕnFчетная.

c) Сумма EnF нечетная и больше 3.

d) Е меньше 6 и F нечетно и больше 1.

e) Е больше 2 и F меньше 4.

f) Е равно 4 и сумма Е и F нечетная.

2. Бросаются независимо две игральные кости и записываются выпавшие числа.

a) Какова вероятность того, что оба числа являются четными?

b) Какова вероятность того, что сумма двух чисел равна 10?

c) Какова вероятность того, что два числа отличаются по меньшей мере на 3?

3. Можно бросать симметричную монету до 7 раз и выиграть 100 долл., если появится по крайней мере три герба до появления решетки. Каковы шансы выиграть 100 долл.?

4. Анна, Джим, Джон и Лиза участвуют в теннисном турнире. Вероятность то­го, что Анна победит Джима, в два раза выше вероятности обратного резуль­тата, а мастерство Джима оценивается на том же уровне, что и мастерство Джона. В прошлом Лиза выигрывала у Джона примерно один раз из трех.

a) Какова вероятность того, что Джим выиграет турнир?

b) Какова вероятность того, что турнир выиграет женщина?

c) Какова вероятность того, что турнир женщина не выиграет?

Глава 12. Основы теории вероятностей

12.1.2. Условные вероятности

Для данных двух событий Е nF условная вероятность события Е при условии, что наступило событие F, обозначается как Р{ Е F} и определяется по формуле

^{P[EIF} =} ^P§} ' ^P[F}>°-

Если событие Е содержится в событии F (т.е. множество исходов Е является под­множеством множества исходов F), тогда P{EF} = Р{Е}.

Два события Е и F являются независимыми тогда и только тогда, когда выпол­няется равенство Р{ Е F} = Р{Е). В этом случае формула условной вероятности сводится к следующему

P{EF}-P{E)P{F).

Пример 12.1.2

Предположим, вы участвуете в игре, в которой другой человек бросает игральную кость. Вы не можете видеть игральную кость, но вам сообщается некоторая инфор­мация об исходах бросания кости. Вам необходимо предсказать возможный исход каждого бросания кости. Определим вероятность того, что исходом будет число 6 при условии, что вам сообщили о том, что исходом бросания кости является четное число.

Пусть Е = {6}; определим F = {2, 4 или 6}. Следовательно,

_Pi_ElF]-llEl-£lE.-iiL-L

^{1 1} ' P{F} P{F} (^) 3'

Заметим, что P{EF} = Р{Е}, так как множество исходов Е является подмножеством множества исходов F.

УПРАЖНЕНИЯ 12.1.3

1. Вернитесь к примеру 12.1.2. Предположим, вам сообщили, что исход броса­ния кости меньше 6.

a) Определите вероятность выпадения четного числа.

b) Определите вероятность выпадения нечетного числа, превышающего 1.

2. Докажите, что если выполняется равенство Р{А В] = Р{А}, то события А и В независимы.

3. Теорема Байеса.¹ Покажите, что для двух заданных событий А и В имеет ме­сто соотношение

Р{ВА}Р{А}

Р{АВ}=- , _л ^{1 1} Р{В}

гдеР{В}>0.

¹ Более детально теорема Байеса представлена в разделе 14.2.2.

12.2. Случайные величины и распределения вероятностей

4. Завод А поставляет в магазин 75 % продаваемых аккумуляторов, а завод В— 25%. Процент бракованных аккумуляторов равен 1 и 2% соответст­венно для заводов А и В. Клиент купил в магазине аккумулятор.

a) Какова вероятность того, что аккумулятор бракованный?

b) Если купленный аккумулятор является бракованным, какова вероят­ность того, что он изготовлен на заводе А? (Совет. Используйте теорему Байеса из предыдущего упражнения.)

5. Статистика свидетельствует, что 70 % мужчин болеют какой-нибудь формой рака предстательной железы. Американский тест PSA в 90 % случаев дает положительный результат для пораженных болезнью мужчин и в 10 % — для здоровых. Какова вероятность того, что мужчина, имеющий положи­тельный результат теста, имеет рак предстательной железы?

12.2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Исходы эксперимента (испытания) обычно либо выражаются в числовом виде, либо им можно поставить в соответствие некоторые действительные числа. Напри­мер, исходы бросания игральной кости выражаются в виде целых чисел от 1 до 6. А проверка на брак некоторого изделия дает два исхода: некачественное и качест­венное. В этом случае можно использовать число 0 для представления исхода "некачественный" и 1 - для исхода "качественный". Численное представление ис­ходов эксперимента — это то, что именуется случайной величиной.²

Случайная величина х может быть дискретной или непрерывной. Например, слу­чайная величина, связанная с бросанием игральной кости, является дискретной со зна­чениями от 1 до 6, тогда как время между поступлениями заявок в систему обслужива­ния выражается непрерывной случайной величиной с положительными значениями.

Как непрерывная, так и дискретная случайная величина имеют плотность рас­пределения вероятностей, которая часто именуется просто плотностью вероятно­сти и обозначается как f(x) (для непрерывной случайной величины) или р(х) (для дискретной случайной величины). Плотности вероятностей должны удовлетворять условиям, перечисленным в следующей таблице.

 

 

 

Характеристики плотности	Случайная величина х
Дискретная	Непрерывная
Область определения	х = а, а+ 1 b	а< х< Ь
Условия неотрицательности	р(х) > 0,	f(x) > 0,
и нормировки		)f{x)dx=l
		«

Условие неотрицательности для непрерывных и дискретных распределений оз­начает, что плотность вероятности не может принимать отрицательные значения (в противном случае вероятность некоторых событий могла бы быть отрицательной).

Случайную величину можно считать функцией, отображающей пространство элемен­тарных исходов на пространство действительных чисел. — Прим. ред.

Глава 12. Основы теории вероятностей

Условие нормировки показывает, что сумма вероятностей по всему пространству событий должна быть равна единице.

Самой важной вероятностной характеристикой случайной величины является функция распределения, определяемая следующим образом:

1'{х< Х} =

Р(Х) = ^р(х) для дискретной случайной величины х,

X

F(X)= ^f(x)dx для непрерывной случайной величиных.

Пример 12.2.1

Рассмотрим ситуацию с бросанием игральной кости. Пусть хе {1, 2, 3, 4, 5,6} — случайная величина, представляющая количество выпавших очков. Тогда плотность вероятности и функция распределения вероятности случайной величины х определяются следующим образом.

р(х) = —, х = 1,2.....6,

Р(Х) = —, Х = 1,2.....6.

На рис. 12.1 приведены графики этих двух функций. Плотность вероятности р(х) является равномерной дискретной функцией, так как любые значения случайной величиной принимаются с одинаковыми вероятностями.

J

----Функция

распределения Р(х)

Плотность вероятности р(х)

Рис. 12.1. Функция распределения и плот­ность вероятности дискретной случайной величины

Непрерывный аналог равномерной плотности вероятности можно получить на ос­нове следующего эксперимента. Стрелка длиной I закреплена подвижно на оси в центре круга, радиус которого также равен I. На окружности выбирается точка отсчета, стрелка вращается в направлении часовой стрелки, по окружности изме­ряется расстояние х, пройденное стрелкой от точки отсчета. Такая случайная вели­чина х является непрерывной, принимающей значения из интервала 0 < х < М. Нет никаких оснований считать, что стрелка будет иметь тенденцию останавливаться в некоторой области окружности чаще, чем в других областях. Поэтому все значения

12.2. Случайные величины и распределения вероятностей

х из интервала 0 < х < М могут приниматься с равной вероятностью и распределение х должно быть равномерным.

В данном случае плотность вероятности f(x) случайной величины х определяется следующим образом.

/(*) = —, 0<х<к1.

Функция распределения F(X) случайной величины х вычисляется по формуле

F(X) = P{x<X} = f— dx=—, 0<Х<к1.

₀^J Л/ Til

На рис. 12.2 представлены графики этих двух функций.

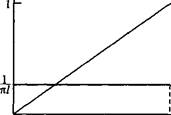
-Функция

распределения F(x)

Плотность вероятности fix)

о к1 х

Рис. 12.2. Функция распределения и плотность ве­роятности непрерывной случайной величины

УПРАЖНЕНИЯ 12.2

1. Некоторая величина принимает случайным образом целочисленное значение х из интервала [1, 5]. Плотность вероятности р(х) этой величины прямо про­порциональна значению х с коэффициентом пропорциональности К.

a) Определите плотность вероятности и функцию распределения данной случайной величины, нарисуйте графики полученных функций.

b) Определите вероятность того, что случайная величина примет значение, равное четному числу.

2. Дана следующая функция:

f(_x) = JL_t 10<д:<20.

X'

a) Найдите значение константы k, при котором функция f(x) будет плотно­стью вероятности.

b) Найдите функцию распределения случайной величины х и определите ве­роятность того, что случайная величина х примет значение: а) больше 12, б) между 13 и 15.

3. Дневная потребность в бензине без свинца является равномерно распреде­ленной случайной величиной, изменяющейся в интервале от 750 до 1250

Глава 12. Основы теории вероятностей

галлонов. Бензоцистерна емкостью 1100 галлонов наполняется ежедневно в полночь. Какова вероятность того, что цистерна будет пустой как раз перед заполнением ее бензином?

12.3. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И МОМЕНТЫ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Пусть х — случайная величина, h(x) — некоторая функция от х. Математиче­ским ожиданием случайной функции h(x), которое обозначается как M{h(x)}, на­зывается средняя величина, взвешенная по отношению к плотности вероятности случайной величины х. При заданной плотности вероятности р(х) или f(x) (для дискретной и непрерывной случайных величин соответственно) величина M{h(x)} вычисляется следующим образом:

M{h(x)}­^Л(х)р(х), если х — дискретная случайная величина,

х=а Ь

^h(x)f[x)dx, если х — непрерывная случайная величина.

Пример 12.3.1

В течение первой недели каждого месяца я, как и большинство людей, оплачиваю все свои счета и отвечаю на некоторые письма. С этой целью я обычно покупаю 20 почтовых марок. Число используемых марок является случайной величиной, при­нимающей значения от 10 до 24 с равными вероятностями. Найдем, чему равно среднее число оставшихся марок.

Пусть х — количество используемых марок, тогда плотность вероятности х такова:

р(х) = —, х = 10,11,..., 24. ^w 15

Количество оставшихся марок определяется соотношением

[20-х, х = 10,11, ...,19,

Следовательно,

4^х)- ,

10 в противном случае.

Л/{Л(х)} = ^[(20-10) + (20-11) + (20-12) + ... + (20-19)] + ^0 = з|.

Произведение у~0 необходимо для завершения вычисления математического ожидания. Вероятность того, что вообще не останется марок, равна

Р{х > 20} = Р(20) + Р(21) + Р(22) + Р(23)+ Р(24) = ⁵f Tj] = 7J-

12.3. Математическое ожидание и моменты случайной величины

УПРАЖНЕНИЯ 12.3.1

1. В задаче из примера 12.3.1 вычислите среднее количество оставшихся марок при условии, что ежемесячно покупается число марок, соответствующее максимально возможной потребности в них.

2. Результаты решения задачи из примера 12.3.1 и предыдущего упражнения приводят к положительным значениям средних величин как при избытке, так и недостаче марок. Являются ли эти результаты противоречивыми? Дай­те объяснение.

3. Владелец газетного киоска каждое утро приобретает для продажи 50 экземп­ляров газеты Аль Ахрам. Ежедневный спрос х на эту газету является случай­ной величиной со следующим распределением

Pixy­

х = 35, 36, ...,49,

х = 50,51.....59,

—, х = 60,61.....70.

a) Найдите вероятность того, что все газеты будут проданы.

b) Вычислите ожидаемое число непроданных газет.

c) Если владелец киоска приобретает газеты за 50 центов, продает за 1 долл., то какова его ожидаемая чистая прибыль в день?

12.3.1. Математическое ожидание и дисперсия случайной величины

Для общей характеристики свойств одномерной случайной величины х обычно используется две числовые характеристики: математическое ожидание (среднее) М{х} и дисперсия D{x}. Математическое ожидание является характеристикой по­ложения распределения случайной величины х на числовой оси относительно на­чала координат, а дисперсия — мерой ее разброса относительно математического ожидания М{х). Большее значение дисперсии свидетельствует о более высокой сте­пени неопределенности в описании случайной величины.

Формулы для математического ожидания и дисперсии случайной величины х могут быть получены из общей формулы для математического ожидания путем подстановкиh(x) = х дляМ{х) иh(x)"(х-М{х})² дляD{x}. Следовательно,

М{Х}­]Г хр (х), если х — дискретная случайная величина,

Ь

jV(x)<£t, если х — непрерывная случайная величина,

Ь ,

^(х-М{х})~ р(х), если а: — дискретная случайная величина, ь

J(x - М {*}) f (x)dx, если х — непрерывная случайная величина.

Обоснованность вывода указанных формул легче просматривается для дискрет­ного распределения. В этом случае М{х) представляет собой взвешенную сумму

Глава 12. Основы теории вероятностей

дискретных значений х, D{x} — взвешенную сумму квадратов отклонения случайной величины х от М{х]. Ситуацию с непрерывно распределенной случайной величиной можно интерпретировать аналогично, заменив суммирование интегрированием.

Пример 12.3.2

Вычислим математическое ожидание и дисперсию для каждого из двух экспери­ментов, рассмотренных в примере 12.2.1.

Ситуация 1 (бросание игральной кости). Здесь плотность вероятности равна

р{х) = —, дг = 1,2,...,6. Следовательно, 6

-и-ШМММИ*)-"-

D{x} = -[(l-3,5)^:+(2-3,5)^:+(3-3,5)²+(4-3,5)²+(5-3,5)²+(6-3,5)²] = 2,917 . Ситуация 2 (вращение стрелки). Пусть длина стрелки равна единице. Тогда

f(x)=-, 0<х<3,14.

^{V ;} 3,14

Математическое ожидание и дисперсия вычисляются следующим образом.

314 .

М{х}= f x-=—dx = ,57 , ¹ ' o^J 3,14

D{x}= /(лг-1,57)² -~dx = 0,822,

УПРАЖНЕНИЯ 12.3.2

1. Вычислите математическое ожидание и дисперсию случайной величины, оп­ределенной в упражнении 12.2.1.1.

2. Вычислите математическое ожидание и дисперсию случайной величины, оп­ределенной в упражнении 12.2.1.2.

3. Покажите, что математическое ожидание и дисперсия случайной величины х, равномерно распределенной на интервале а < х < Ь, равны

, Ь + а ^{1 ;} 2

„_г , (Ь-а)^г

4. Докажите, что для случайной величины х, определенной на интервале а < х < Ь с заданной плотностью вероятности f(x), имеет место соотношение

D{x} = M{x²}-(M{x}f.

12.3. Математическое ожидание и моменты случайной величины

5. Пусть для случайной величины х, определенной на интервале а < х < Ь, зада­на плотность вероятности f(x) иу^сх + d, где end — константы. Докажите, что имеют место соотношения

M{y} = cM{x} + d, D{y} = c-D{x}.

12.3.2. Совместные распределения вероятностей

Рассмотрим две непрерывно распределенные случайные величины х^ и х₂, кото­рые определены соответственно на интервалах а, < х, < 6, и а₂ < х_г < Ь_г. Обозначим через f(x_v х₂) плотность совместного распределения вероятностей величин х, и х₂, а через /,(*,) и f₂(x₂) — маргинальные (частные) плотности распределения вероят­ностей величин ас, и х₂ соответственно. Тогда

/(лг,,х,)>0, a, <x,<b_v a₂<x₂<b₂, Jfifr, fa₂f(x_l,x₂) = l

b.

/iW= f{x„x₂)dx₂,

fi(^xi) = f(x_vx,)dx_t,

f(x_vx₂) = f_x{x_x)f₁{x₂), если*, нх₂ независимы.

Такие же формулы используются для дискретно распределенных случайных вели­чин, которые получаются в результате замены интегрирования суммированием.

Далее в этом разделе рассматриваются функции от нескольких случайных пе­ременных. В частности, рассмотрим две ситуации.

1. у = х₁х₁,

2. у = с,лг, +с₂х₂,

где х,иа:_г — случайные величины, плотность совместного распределения вероят­ностей которых задана функцией /(х„ х₂).

Если х, и х₂ независимые случайные величины, то

М{х,х₂)=М{х,)М{х₂).

Для суммы случайных величин х, и х_г без учета их зависимости можно доказать, что

М{с,х, + с₂х₂) = c_lM{x_l) + с₂М{х₂).

Кроме того,

Z5{c,jt, + с,*,} = c;D{x_l} + c;D{x₂} + 2c,c,cov {я,,*,}, где ковариация covfxp x₂) случайных величин и x₂ вычисляется по формуле

Глава 12. Основы теории вероятностей

cov[x_vx₂} = М{(*, -М{x_t})(x₂ -М{*,})} = Мх_хх_г -х,М[х₂}~х_гМ{х,} + М{х_х}М{х₂}} = = М{х₁х,}-М{х₁}М{х,}.

Если x; и х₂— независимые случайные величины, то М{х,х₂} = М{х^М{х₂) hcov{x,, х_г) = 0. Обратное утверждение неверно в том смысле, что две зависимые случайные величины могут иметь ковариацию, равную нулю.

Пример 12.3.3

Партия изделий содержит четыре дефектных (Д) и шесть качественных (К) изде­лий. Случайным образом выбирается и проверяется одно изделие. Затем, не воз­вращая его, выбирают и тестируют другое. Пусть случайные величины х, и х₂ пред­ставляют исходы тестирования первого и второго изделий соответственно.

1. Определим плотность совместного распределения вероятностей случайных величин х, и х₂.

2. Найдем маргинальную плотность вероятности случайной величины х₂.

3. Предположим, мы получаем 5 долл. за каждое качественное изделие из вы­бранных и платим 6 долл., если изделие бракованное. Найдем математиче­ское ожидание и дисперсию выигрыша после двух испытаний.

Обозначим через р(х_р х₂) плотность совместного распределения вероятностей слу­чайных величин х, и х₂, а через рДх,) и р₂(х₂) — их маргинальные плотности веро­ятностей. Определим сначалар,(х,) как

Мы знаем, что исход х₂ второго испытания зависит от х,. По этой причине для оп­ределения р₂(х₂) сначала определим плотность р(х_и х₂) совместного распределения вероятностей случайных величин х, и х₂, после чего можно будет определить мар­гинальную плотность вероятности р₂(х₂). Имеем

Для определения р(х,, х₂) воспользуемся формулой Р{АВ} = Р{А | В}Р{В} (см. раздел 12.1.2). Получаем следующее.

_Pi(K) = — = 0,

⁶> а(Д)=т!т⁼⁰'⁴-

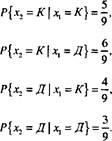
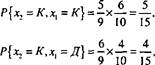
12.3. Математическое ожидание и моменты случайной величины

Представим теперь плотность совместного распределения следующим образом.

		х2 = К	х2=Д
Р(хьхг) =	х,=К	5/15	4/15	9/15
		4/15	2/15	6/15
	Рг(х2)	9/15	6/15

Маргинальные плотности распределения вероятностей p,(#i) и р₂(х₂) могут быть оп­ределены посредством суммирования элементов (соответственно) столбцов или строк в таблице, представляющей значения плотности совместного распределения. Интересно отметить, что, вопреки интуиции, здесь/>₁(jc₁) = р_г(х₂).

Математическое ожидание выигрыша можно определить из совместного распреде­ления, если принять, что изделие К дает 5 долл., а изделие Д — 6. Следовательно,

ожидаемый выигрыш = (5 +^)^~j⁺ ~**)^^j⁺

₊ (^ ₊ 5)(±) ₊ H-6)(2) = U0.

Тот же результат можем получить, принимая во внимание, что математическое ожидание выигрыша после двух испытаний равно сумме математических ожида­ний после каждого испытания в отдельности.

ожидаемый выигрыш =(ожидаемый выигрыш после 1-го испытания)+

+(ожидаемый выигрыш после 2-го испытаиия)=

= 0,60 + 0,60 = 1,20.

Для вычисления дисперсии общего выигрыша заметим, что

2){выигрыша} = £){1-го выигрыша} + £){2-го выигрыша} +

+ 2cov{l-ro выигрыша, 2-го выигрыша}.

Так как р,(х,) = р₂(х₂), то D{l-ro выигрыша} = D{2-ro выигрыша}. Для вычисления дисперсии воспользуемся формулой

D{x)=M{x²}-(M{x})

Следовательно,

£){1-го выигрыша} =

-0, б² =29,04.

Далее для вычисления ковариации применим формулу

cov{x_l,x₂} = М {х^х₂}-М {х^М {х_г}.

Глава 12. Основы теории вероятностей

При вычислении значения М{х₁х₂) нужно знать плотность совместного распределе­ния вероятностей случайных величин х_х и х₂. Имеем

ковариация^:

-0,6x0,6 = -3,23.

Итак,

дисперсия = 29,04 + 29,04 + 2(-3,23) = 51,62.

УПРАЖНЕНИЕ 12.3.3

1. Плотность совместного распределения вероятностей p(x_v х₂) случайных ве­личин х, и х₂ имеет следующий вид.

		x2 = 3	х2 = 5	Х2=7
	х, = 1	0,2		0,2
p(Xi, х2) =	х, =2		0,2
	Xi = 3	0,2		0,2

a) Найдите маргинальные плотности вероятностейр,(х,) ир₂(х₂).

b) Являются ли случайные величины х_х и х₂ независимыми?

c) Вычислите М{х_х + х₂). А) Найдите cov{x,, х₂).

е) Вычислите D{5x, - 6х₂}.

12.4. НЕКОТОРЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

В разделах 12.2 и 12.3 мы рассмотрели равномерные распределения (дискретные и непрерывные). В этом разделе рассматриваются еще четыре распре­деления случайных величин, которые часто используются в теории исследования операций, — дискретные (биномиальное и Пуассона) и непрерывные (экспоненциальное и нормальное).

12.4.1. Биномиальное распределение

Предположим, предприниматель изготавливает некоторые изделия партиями по п единиц в каждой. Предыдущий опыт свидетельствует, что вероятность появ­ления бракованного изделия в каждой партии равна р. Необходимо определить плотность вероятности числа бракованных изделий в партии.

тт „X Х(П~Х)

Имеется С* = ⁴ —— различных возможностей получить х бракованных изде­лий в партии из п изделий; вероятность реализации каждой такой комбинации равна р*(1 -р)"~". Отсюда следует, что вероятность того, что в партии из п изделий имеется k бракованных, равна (что следует из закона сложения вероятностей)

Р{х = к} = С^к„р^к(1-_Р)"- к =1,2,..., п.

12.4. Некоторые распределения вероятностей

Это формула плотности вероятности биномиального распределения с параметрами пир. Математическое ожидание и дисперсия для этого распределения равны

М{х) = пр, D{x) - гер(1 -р).

Пример 12.4.1

Некая работа сопряжена с десятью поездками на автомобиле между двумя городами. Выполнив все 10 поездок, работник может отдыхать остаток дня, что является доста­точным стимулом для превышения скорости. Опыт показывает, что вероятность полу­чения штрафа за превышение скорости в каждой поездке туда и обратно равна 40 %.

1. Какова вероятность того, что рабочий день закончится без получения штрафа?

2. Если штраф равен 150 долл., то каково среднее значение дневного штрафа?

Вероятность быть оштрафованным в одной поездке равна р = 0,4. Следовательно, вероятность того, что рабочий день закончится без штрафа, равна

р{_х = 0} = С° (0,4)" (0,б)¹⁰ = 0,006047.

Это значит, что шанс закончить рабочий день без штрафа меньше одного процента. Средний штраф = 150М{*} = 80(гер) = 80 х10 х 0,4 = 320 (долл.).

УПРАЖНЕНИЯ 12.4.1

1. Симметричная игральная кость бросается 10 раз. Какова вероятность того, что ни разу не выпадет четное число очков?

2. Пусть независимо бросаются пять симметричных монет. Какова вероятность того, что в точности одна из монет выпадет одной стороной, а остальные че­тыре — другой?

3. Гадалка утверждает, что по почерку она может предсказать, достигнет ли чело­век благосостояния на протяжении всей своей жизни. Для проверки этого попро­сили 10 миллионеров и 10 профессоров предоставить образцы их почерка. Затем эти образцы были представлены гадалке попарно — по одной подписи миллио­нера и профессора в каждой паре. Считается, что утверждение гадалки является правильным, если она сделала по меньшей мере восемь правильных предска­заний. Какова вероятность того, что утверждение гадалки будет "удачным"?

4. Казино предлагает следующую игру. Вы, игрок, выбираете число от 1 до 6. Затем одновременно бросаются три игральные кости. Казино вам выплачи­вает столько долларов, сколько будет совпадений на костях с вашим выбран­ным числом. Если таких совпадений нет, то вы платите казино 1 долл. Каков ваш долговременный ожидаемый выигрыш в этой игре?

5. Предположим, что вы играете в следующую игру. Вы бросаете две игральные кости. Если выпавшие числа на костях различные, то вы теряете 10 центов. Если же эти числа совпадают, то вы получаете 50 центов. Каков ожидаемый выигрыш в этой игре?

6. Докажите приведенные выше формулы для математического ожидания и дисперсии биномиального распределения.

Глава 12. Основы теории вероятностей

12.4.2. Распределение Пуассона

Люди приходят в банк или магазин "совершенно случайным" образом. Это означа­ет, что нет никакой возможности предсказать, когда и кто придет. Плотность вероятно­сти случайной величины, которая равна количеству таких посещений на протяжении определенного периода времени, описывается с помощью распределения Пуассона.

Пусть х— количество событий (например, посещений банка или магазина), которые происходят на протяжении единицы времени (например, минуты или часа). Плотность вероятности распределения Пуассона задается формулой

Р{_х = к} = ^—, 4 = 1,2,....

Математическое ожидание и дисперсия распределения Пуассона равны соответ­ственно М{х) = Я и D{x) = Я. Из интуитивных соображений формула М{х) — Я долж­на означать среднее количество событий, происходящих за единицу времени. По существу, это так и есть: параметр Я определяет скорость, с которой происходят со­бытия (количество событий за единицу времени).

Распределение Пуассона широко используется в теории массового обслужива­ния (см. главу 17).

Пример 12.4.2

Заказы на ремонт небольших электродвигателей поступают в мастерскую случай­ным образом, примерно 10 заказов в день.

1. Каково среднее количество электродвигателей, которые поступают ежеднев­но в мастерскую?

2. Какова вероятность того, что на протяжении одного часа не поступит ни од­ного заказа, если мастерская открыта 8 часов в день?

Среднее количество заказов, которые поступают ежедневно в мастерскую, равно Я= 10. Для вычисления вероятности того, что на протяжении одного часа не посту­пит ни одного заказа, необходимо подсчитать скорость поступления заказов в час, т.е. в среднем Х_час = 10/8 = 1,25 заказа в час. Следовательно,

Р{нет заказов за 1 час} = -= —-= 0,2865.

^{1 1} 01 1

УПРАЖНЕНИЯ 12.4.2

1. Клиенты прибывают в учреждение обслуживания в соответствии с распреде­лением Пуассона со скоростью четыре клиента в минуту. Какова вероятность того, что по крайней мере один клиент прибудет в любой заданный 30-секундный интервал времени?

2. Распределение Пуассона с параметром Я аппроксимирует биномиальное распределение с параметрами пир при условии, что п — достаточно большое положительное число, р — очень малое число, а Я примерно равно пр (с математической точки зрения это означает, что п —> °°, р -» О и пр —> Я). Продемонстрируйте это на ситуации, когда известно, что изго­

12.4. Некоторые распределения вероятностей

товленная партия изделий содержит 1% брака. Вычислите вероятность того, что выборка объемом 10 изделий содержит не более одного брако­ванного изделия, использовав для этого сначала (точное) биномиальное распределение, а затем (приближенное) распределение Пуассона. Пока­жите, что такое приближение будет неприемлемым, если величина р бу­дет увеличена, скажем, до 0,5.

3. Покупатели подходят к контрольной кассе со средней интенсивностью 20 че­ловек в час.

a) Найдите вероятность того, что касса будет свободной.

b) Какова вероятность того, что в очереди перед кассой будет не менее 2 че­ловек?

4. Докажите приведенные выше формулы для математического ожидания и дисперсии распределения Пуассона.

12.4.3. Отрицательное экспоненциальное распределение

Если число заявок, поступивших в учреждение за определенный период време­ни, удовлетворяет распределению Пуассона, то распределение интервалов времени между последовательными поступлениями заявок должно следовать отрицатель­ному экспоненциальному (или просто экспоненциальному) распределению. В част­ности, если X есть скорость появления событий в распределении Пуассона, то рас­пределение времени х между последовательными поступлениями определяется плотностью вероятности

f(x) = Xe'^, х>0. На рис. 12.3 показан график функции f(x).

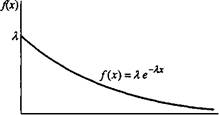
Рис. 12.3. Плотность вероятности экс­поненциального распределения

Математическое ожидание и дисперсия экспоненциального распределения равны

М{4 = 1 D{x} = ±

Математическое ожидание М{х} согласуется с определением X. Если X — скорость, с которой происходят события, то 1/Х— средний интервал времени между после­довательными событиями.

Глава 12. Основы теории вероятностей

Пример 12.4.3

Автомобили прибывают на заправочную станцию случайно, в среднем каждые 2 минуты. Вычислите вероятность того, что интервал между последовательными прибытиями автомобилей не превысит 1 минуты.

Искомая вероятность имеет вид Р{х<А}, здесь А = 1 минута. Вычисление требуе­мой вероятности эквивалентно вычислению значения функции распределения слу­чайной величины х.

л

Р{х < А} = jXe^dx = -е^ |₀^Л = 1 - е~^и. о

Вычисляем скорость прибытия автомобилей.

X = -i прибытия в минуту.

Следовательно,

Р{х<1} = 1-е"'⁰' =0,39.

УПРАЖНЕНИЯ 12.4.3

1. Магазин посещают жители как городской местности, так и сельской. Город­ские покупатели прибывают со скоростью 5 посетителей в минуту, а сель­ские — 7 посетителей в минуту. Прибытия покупателей являются случай­ными событиями. Определите вероятность того, что время между последовательными прибытиями посетителей будет меньше 5 секунд.

2. Докажите приведенные выше формулы для математического ожидания и дисперсии экспоненциального распределения.

12.4.4. Нормальное распределение

Нормальное распределение описывает многие случайные явления, которые происходят в каждодневной жизни, включая анализ счетов, распределение веса и роста людей и многое другое. Плотность вероятности нормального распределения задается формулой

f[x) = —F=e ^2al , -~ < х < ~,

где М{х] = /л, D{x) = d'. Нормальное распределение с математическим ожиданием // и стандартным отклонением собозначается как N(/u, о).

На рис. 12.4 показан график плотности f(x) нормального распределения. Как видим, плотность вероятности является симметричной функцией относительно ма­тематического ожидания ц.

12.4. Некоторые распределения вероятностей

Рис. 12.4. Плотность вероятности нор­мального распределения

Важность нормального распределения объясняется тем, что распределение среднего достаточно большой выборки, имеющей любое распределение, можно асимптотически аппроксимировать нормальным распределением. Это следует из представленной ниже теоремы.

Центральная предельная теорема. Пусть ...,*„ — независимые, одинаково

распределенные случайные величины с математическим ожиданием /и и стан­дартным отклонением акаждая. Определим сумму

s_tl = x_t+x₂ +... + х„.

При возрастании п (п -»°°) распределение случайной величины s_n является асимптотически нормальным с математическим ожиданием пц и дисперсией пс? независимо от начального распределения величин x_vx₂,...,x„.

Центральная предельная теорема свидетельствует, в частности, о том, что сред­нее выборки объемом ге, имеющей любое распределение, асимптотически является нормальным с математическим ожиданием jun дисперсией с?/п.

Функцию нормального распределения трудно представить в виде формулы, пригодной для практических расчетов. В связи с этим составлены специальные таблицы функции нормального распределения (см. табл. 1 в приложении В). Эти таблицы созданы для стандартного нормального распределения с нулевым мате­матическим ожиданием и дисперсией, равной единице. Любую нормально распре­деленную случайную величину х с математическим ожиданием ц и дисперсией о² можно привести к стандартному виду путем замены

о

Отметим, что около 99 % площади под кривой плотности нормального распре­деления находится в интервале ц-Ъо<х< ц+Ъо. Этот факт известен под названи­ем "правило трех сигм".

Пример 12.4.4

Внутренний диаметр цилиндра должен иметь размер (спецификацию) 1±0,3 дюй­ма. Процесс механической обработки таких деталей подчиняется нормальному распределению с математическим ожиданием 1 и стандартным отклонением 0,1 дюйма. Требуется определить процент продукции, удовлетворяющей требованиям спецификации.

Глава 12. Основы теории вероятностей

Пусть случайная величина д: равна диаметру цилиндра. Вероятность того, что ци­линдр будет удовлетворять требованиям спецификации, равна

Р{1 - 0,03 < х < 1 + 0,03} = Р{0,97 < х < 1,03}.

При //=1и а= 0,1 эту вероятность можно выразить через стандартное нормальное распределение следующим способом.

Р{0,97 < х < 1,03} = Р|^р * z £= Р{-0,3 S z < 0,3} =

= P{z < 0,3} - P{z < -0,3} = P{z < 0,3} -[l - P{z < 0,3}] = = 2P{z < 0,3} -1 = 2x0,6179-1 = 0,2358.

На рис. 12.5 заштрихованная область соответствует искомой вероятности. Заме­тим, что равенство Р{г < -0,3} = 1 - P{z < 0,3} имеет место в силу симметрии функ­ции плотности вероятностей. Величина 0,6179 (=Р{г<0,3}) взята из таблицы для нормального распределения (табл. 1 приложения В).

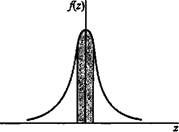
-0,3 0 0,3

Рис. 12.5. Вычисление вероятно­сти Р{-0,3<х<0,3} стандарт­ного нормального распределения

УПРАЖНЕНИЯ 12.4.4

1. Инженерный колледж американского университета набирает студентов из числа выпускников средней школы, которые по стандартному тесту ACT для поступающих в колледжи имеют не менее 26 баллов. Результаты тестирования выпускников являются нормально распределенной случайной величиной с ма­тематическим ожиданием 22 балла и стандартным отклонением 2 балла.

a) Определите процент выпускников средней школы, которые являются по­тенциальными студентами инженерного колледжа.

b) Определите процент выпускников школы, которые не будут приняты в инженерный колледж, если университет не примет ни одного из них с количеством баллов, меньше 17.

2. Вес людей, которые хотят совершить прогулку на вертолете в парке аттрак­ционов, является случайной величиной с математическим ожиданием 180 фунтов и стандартным отклонением 15 фунтов. Вместимость вертолета со­ставляет пять человек, максимальная грузоподъемность — 1000 фунтов. Какова вероятность того, что вертолет не взлетит с пятью пассажирами на борту? (Совет. Используйте центральную предельную теорему.)

12.5. Эмпирические распределения

3. Внутренний диаметр цилиндра является нормально распределенной случай­ной величиной с математическим ожиданием 1 дюйм и стандартным отклоне­нием 0,01 дюйма. При сборке внутрь каждого цилиндра вставляется твердый стержень. Диаметр стержня является нормально распределенной случайной величиной с математическим ожиданием 0,99 и стандартным отклонением 0,01 дюйма. Требуется определить процент пар цилиндр-стержень, которые не подойдут для сборки. (Подсказка. Разность двух нормально распределенных случайных величин также является нормально распределенной величиной.)

12.5. ЭМПИРИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ

В предыдущих разделах мы рассмотрели свойства плотностей вероятностей, функции распределения случайных величин и привели примеры четырех типов распределений. Как определяются эти распределения на практике?

Определение (или, точнее, оценка) любой плотности вероятности случайной ве­личины содержится в необработанной информации, которая собирается в процессе изучения исследуемой ситуации. Например, для оценки плотности вероятности времени между приходом покупателей в бакалейную лавку, сначала фиксируется время их прихода. Искомое время между приходом покупателей находится путем вычитания времен последовательных их приходов.

В этом разделе мы рассмотрим, как собранные данные (именуемые статисти­ческим рядом или выборкой) можно преобразовать в плотность вероятности слу­чайных величин с помощью следующих шагов.

Шаг 1. Отображаем данные в виде подходящей частотной гистограммы и подбираем эмпирическую функцию плотности вероятности.

Шаг 2. Используем критерий согласия, чтобы проверить, совпадает ли полученная эмпирическая функция плотности вероятности с од­ной из известных плотностей вероятностей.

Рассмотрим детали этой процедуры.

Гистограмма частот. Данная гистограмма строится на основе статистического ряда (выборки) путем деления области изменения исходных данных (от минималь­ного до максимального значения) на непересекающиеся интервалы. При заданных границах (1^, I) интервала i соответствующая частота определяется как число вы­борочных значений х, которые удовлетворяют неравенству <x<I_t.

Пример 12.5.1

Данные, приведенные в следующей таблице, представляют время обслуживания (в минутах) 60 посетителей в некотором сервисном центре.

	0,4	3,4	4,8	2,0	1,0	5,5	6,2	1,2	4,4
1,5	2,4	3,4	6,4	3,7	4,8	2,5	5,5	0,3	8,7
2,7	0,4	2,2	2,4	0,5	1.7	9,3	8,0	4,7	5,9
0,7	1,6	5,2	0,6	0,9	3,9	3,3	0,2	0,2	4,9
9,6	1,9	9,1	1,3	10,6	3,0	0,3	2,9	2,9	4,8
8,7	2,4	7,2	1,5	7,9	11,7	6,3	3,8	6,9	5,3

Глава 12. Основы теории вероятностей

Минимальное и максимальное значения приведенных данных соответственно рав­ны 0,2 и 11,7. Поэтому выбираем двенадцать интервалов длиной в 1 минуту (полный интервал изменений равен [0,12]). Надлежащий выбор размера интервала является решающим фактором в определении формы эмпирического распределе­ния. Хотя не существует жестких правил выбора оптимального размера интервала, общим правилом, которого следует придерживаться, является выбор от 10 до 20 интервалов. На практике было бы неплохо попробовать различные размеры интер­вала для построения подходящей гистограммы.

Приведенная ниже таблица суммирует информацию для рассматриваемого стати­стического ряда, необходимую для построения гистограммы. Столбец относитель­ной частоты /, вычисляется путем деления соответствующих значений столбца час­тоты о, на общий объем наблюдений (ге = 60). Например Д = 11/60= 0,1833. Значения F_t в столбце накопленных частот вычисляются посредством последова­тельного суммирования величин f_t. Так, F₁ = f_l= 0,1833 и F₂ = F₁ + f₂ = = 0,1833 + 0,1333 = 0,3166.

Интервал	Подсчет наблюдений	Частота, о,	Относительная частота, f,	Накопленная относительная частота, F,
(0, 1)	4Ш--ШН		0,1833	0,1833
(1.2)	-ШИП		0,1333	0,3166
(2,3)	ш НИ		0,1500	0,4666
(3,4)	Ш II		0,1167	0,5833
(4, 5)	ш		0,1000	0,6833
(5,6)	4W-		0,0833	0,7666
(6,7)	IIII		0,0667	0,8333
(7,8)	II		0,0333	0,8666
(8,9)	III		0,0500	0,9166
(9, Ю)	III		0,0500	0,9666
(10, 11)	I		0,0167	0,9833
(11,12)	I		0,0167	1,0000
Всего			1,0000

Величины и F_t являются дискретными эквивалентами плотности вероятности и функции распределения времени обслуживания t. Так как гистограмма частот дает дискретную версию непрерывного времени обслуживания, можно преобразовать дискретную функцию распределения в непрерывную кусочно-линейную функцию, соединяя полученные точки отрезками прямых. На рис. 12.6 представлена эмпири­ческая плотность вероятности и функция распределения для рассматриваемого приме­ра. Здесь функция распределения оценивается в средних точках интервалов значений.

Теперь можно оценить математическое ожидание Г и дисперсию sf эмпирического распределения. Пусть N— число интервалов в гистограмме; обозначим через среднюю точку интервала L Тогда

12.5. Эмпирические распределения

0.2

0.4

0.6

0.8

1.0