От В Уд. стоимость

100 30 9999 9999 9999 30 9999 9999

1 9999

2 9999

4 10

5 60

1 9999

2 15

Поиск решения

Установить целевую ячейку:

1*8*18

Равной: <~

максимальному значению

ЭНЭЧбНИ'О

Выполнить 1 Закрыть I

^с минимальному значению Иэменая ячейки.

|$B*20:$S$39

Ограничения.

$F*19:$F$23 = $G$19:$G$23

"31 Предположить |

ры {

До&аеить

Изменить

J

У_далить

Параметры

Восстановить

Справка

Рис. 6.26. Вычисление кратчайшего пути в Excel

На рис. 6.26 строки от 11 до 15 и столбец К скрыты для экономии места.

6.4. Задача о максимальном потоке

После того как будут введены значения спроса и предложения, рабочий лист пе-ресчитывается автоматически. Выделенные столбцы В, С, F и G содержат исходные данные задачи, необходимые для использования средства Поиск решения. Диапа­зон В20:В39 (изменяемые ячейки для средства Поиск решения) содержит величины потоков, проходящие по каждой дуге. Столбец С содержит значение пропускных способностей дуг (диапазон С20:С39). В задаче поиска кратчайшего пути эти про­пускные способности в вычислениях не участвуют, поэтому они имеют "бесконечные" значения (равные 99999). Ограничения модели представляют ба­лансы потоков, проходящих через каждый узел. Как показано в разделе 5.3.3, с помощью функций СУММЕСЛИ вычисляются чистые потоки через каждый узел, для чего используются данные из столбцов I и J. Все эти вычисления выполняются автоматически. Все, что необходимо сделать вам для решения задачи, — это ука­зать диапазон изменяемых ячеек и задать ограничения в диалоговом окне средства Поиск решения. На рис. 6.26 видно, что изменяемые ячейки составляют диапазон В20:В39, а ограничения задаются в виде равенства F19:F23=G19:G23.

Решение N1-N3 = 1, N3-N4 = 1 и N4-N2 = 1, показанное на рис. 6.26, дает общее расстояние 55 миль. Это решение означает, что кратчайший путь проходит через узлы 1 -» 3 —> 4 —> 2.

УПРАЖНЕНИЯ 6.3.5

1. Измените рабочую книгу ch6SolverShortestRoute.xls применительно к задаче примера 6.3.4, чтобы найти кратчайшие пути между следующими парами узлов.

a) От узла 1 до узла 5.

b) От узла 4 до узла 3.

2. Измените рабочую книгу ch6SolverShortestRoute.xls применительно к задаче из упражнения 6.3.1.2, чтобы найти кратчайший путь между узлами 4 и 7.

6.4. ЗАДАЧА О МАКСИМАЛЬНОМ ПОТОКЕ

Рассмотрим сеть трубопроводов для транспортировки сырой нефти от буровых скважин до нефтеперегонных заводов. Для перекачки нефти предусмотрены магист­ральные насосные станции. Каждый сегмент трубопровода имеет свою пропускную способность. Сегменты трубопровода могут быть как однонаправленные (осуществляют перекачку нефти только в одном направлении), так и двунаправлен­ные. В однонаправленных сегментах положительная пропускная способность пред­полагается в одном направлении и нулевая — в другом. На рис. 6.27 показана типо­вая сеть нефтепроводов. Как определить максимальную пропускную способность (т.е. максимальный поток) между нефтяными скважинами и нефтеперегонными заводами?

При решении данной задачи исходную сеть необходимо свести к сети с одним источником и одним стоком. Этого можно достичь, вводя дополнительные дуги с бесконечной пропускной способностью от источника к скважинам и от нефтепере­гонных заводов к стоку (на рис. 6.27 эти дуги показаны пунктирными линиями).

Для ребра (/, у), где i < у, используем запись (С^,С_у,) для представления пропуск­ных способностей в направлениях i —> у и у —> i соответственно. Во избежание недо­разумений на схеме сети С. будем располагать на ребре (t, у) ближе к узлу i, a C_jt — ближе к узлу у, как показано на рис. 6.28.

Глава 6. Сетевые модели

Источник''"^

■Скважиньп Насосные станции i Нефте­перегонные' заводы

Рис. 6.27. Сеть, связывающая скважины, насосные станции и нефтеперегонные заводы

-4D

Рис. 6.28. Обозначение пропускных способностей

6.4.1. Перебор разрезов

Разрез определяет множество ребер, при удалении которых из сети полностью прекращается поток от источника к стоку. Пропускная способность разреза равна сумме пропускных способностей "разрезанных" ребер. Среди всех разрезов сети раз­рез с минимальной пропускной способностью определяет максимальный поток в сети.

Пример 6.4.1

Рассмотрим сеть, показанную на рис. 6.29. На этом рисунке при обозначении про­пускных способностей двунаправленных ребер придерживались соглашения, при­нятого ранее (рис. 6.28). Например, для ребра (3, 4) пропускная способность в на­правлении 3 —> 4 равна 10, а в направлении 4 —> 3 — только 5. >*

Разрез 2

Рис. 6.29. Пример разрезов сети

6.4. Задача о максимальном потоке 271

Разрезы, представленные на рис. 6.29, имеют следующие пропускные способности.

Разрез	"Разрезанные" ребра	Пропускная способность
	(1,2), (1.3), (1,4)	10 + 30 + 20 =60
	(1,3), (1,4), (2, 3), (2, 5)	30 + 10 + 40 + 30 = 110
	(2, 5), (3, 5), (4, 5)	30 + 20 + 20 = 70

Вывод, который можно сделать на основе этих трех разрезов, заключается в том, что максимальный поток не может превышать 60 единиц. Но мы не можем сказать, каков максимальный поток на самом деле, так как не перебрали все возможные разрезы сети. К сожалению, перебор всех разрезов является непростой задачей. По­этому для определения максимального потока в сети не используются алгоритмы, основанные на полном переборе разрезов. В следующем разделе будет показан эф­фективный алгоритм вычисления максимального потока.

УПРАЖНЕНИЕ 6.4.1

1. Для сети, показанной на рис. 6.29, проведите еще два разреза и найдите их пропускные способности.

6.4.2. Алгоритм нахождения максимального потока

Идея данного алгоритма состоит в поиске сквозных путей с положительными потоками от источника к стоку.

Рассмотрим ребро (i, у) с (начальной) пропускной способностью (С..С,,). В про­цессе выполнения алгоритма части этих пропускных способностей "забираются" потоками, проходящими через данное ребро, в результате каждое ребро будет иметь остаточную пропускную способность. Будем использовать запись (с_ц, с,) для представления остаточных пропускных способностей. Сеть, в которой все ребра имеют остаточную пропускную способность, назовем остаточной.

Для произвольного узла у, получающего поток от узла i, определим метку [а_у, Л, где а — величина потока, протекающего от узла у к узлу i. Чтобы найти макси­мальный поток, выполним следующие действия.

Этап 1. Для всех ребер (t, у) положим остаточную пропускную способность равной первоначальной пропускной способности, т.е. приравняем (с, с^ = (С^,С_;,) . Назначим а, = оо и пометим узел 1 меткой [оо, —]. Полагаем i = 1 и переходим ко второму этапу.

Этап 2. Определяем множество S_l как множество узлов у, в которые можно перейти из узла i по ребру с положительной остаточной пропуск­ной способностью (т.е. с, > 0 для всех у 6 S_t). Если S, ф 0, выполня­ем третий этап, в противном случае переходим к п. 4.

Этап 3. В множестве S_l находим узел к, такой, что

Положим а_к = с_1к и пометим узел к меткой [а_к, П. Если последней меткой помечен узел стока (т.е. если к = п), сквозной путь найден,

Глава 6. Сетевые модели

и мы переходим к пятому этапу. В противном случае полагаем i = kvL возвращаемся к п. 2.

Этап 4. Откат назад. Если i = 1, сквозной путь невозможен, и мы перехо­дим к п. 6. Если находим помеченный узел г, непосредствен­но предшествующий узлу I, и удаляем узел i из множества узлов, смежных с узлом г. Полагаем i = г и возвращаемся ко второму этапу.

Этап 5. Определение остаточной сети. Обозначим через N = {1, k_v k₂, п) множество узлов, через которые проходит р-й найденный сквозной путь от узла источника (узел 1) до узла стока (узел п). Тогда макси­мальный поток, проходящий по этому пути, вычисляется как

/, = min{o„o„,o_H> ...,а„}.

Остаточные пропускные способности ребер, составляющих сквоз­ной путь, уменьшаются на величину / в направлении движения потока и увеличиваются на эту же величину в противоположном направлении. Таким образом, для ребра (£,j), входящего в сквоз­ной путь, текущие остаточные пропускные способности (c_t/, c_jt) из­менятся следующим образом:

a) (с„ ~ /_р. с + /„)> если поток идет от узла i к узлу

b) (с_ч + f , c_/t - f_p), если поток идет от узлаj к узлу L

Далее восстанавливаем все узлы, удаленные в п. 4. Полагаем i — 1 и возвращаемся ко второму этапу для поиска нового сквозного пути.

Этап 6. Решение.

a) При т найденных сквозных путях максимальный поток вы­числяется по формуле

F = f_l+f₂ + ...+f_m.

b) Имея значения начальных (C_v,C_ji) и конечных (с,., с.,) пропуск­ных способностей ребра (i, /'), можно вычислить оптимальный поток через это ребро следующим образом. Положим (а,р) = (С_(/-с,_у,С_у1-с_>,). Если а > 0, поток, проходящий через

ребро (i, j), равен а. Если же Р > 0, тогда поток равен р. (Случай, когда одновременно а > 0 и р > 0, невозможен.)

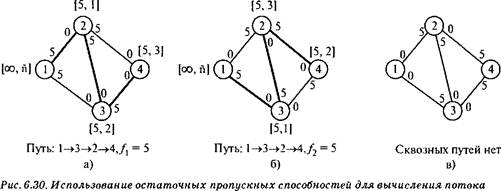
Процесс отката назад на четвертом этапе выполняется тогда, когда алгоритм должен "убить" промежуточный узел до момента реализации сквозного пути. Кор­рекцию пропускных способностей, выполняемых в п. 5, можно пояснить на приме­ре простой сети, показанной на рис. 6.30. На рис. 6.30, а найден первый сквозной путь N_l — {1, 2, 3, 4} с максимальным потоком /, = 5. После этого остаточные пропу­скные способности ребер (1, 2), (2, 3) и (3, 4) изменятся соответственно с (5, 0) на (0, 5). На рис. 6.30, б показан второй сквозной путь N₂ = {1, 3, 2, 4} с максимальным потоком /₂ = 5. После коррекции пропускных способностей получаем сеть, пока­занную на рис. 6.30, в, где уже невозможно построить сквозной путь. Почему так получилось? При вычислении остаточных пропускных способностей в п. 5 при пе­реходе от сети б к сети в невозможна организация потока в направлении 2 -> 3. По­лучается, что алгоритм как бы "помнит", что поток в направлении 2 -> 3 уже был в предыдущих сквозных путях, и поэтому снова (на пятом этапе) изменяет пропу­скную способность с 0 до 5 в направлении от узла 3 к узлу 2.

6.4. Задача о максимальном потоке

Пример 6.4.2

Найдем максимальный поток в сети из примера 6.4.1 (рис. 6.29). На рис. 6.31 предлагается графическая иллюстрация выполнения алгоритма. Считаем полез­ным сравнить описание выполняемых алгоритмом вычислительных итераций с их графическим представлением.

Итерация 1. Положим остаточные пропускные способности (c_i;, c_Jt) всех ребер рав­ными первоначальным пропускным способностям (C_irC_n) ■

Шаг 1. Назначаем я, = оо и помечаем узел 1 меткой [оо, —]. Полагаем ( = 1. Шаг 2. S, = (2, 3, 4} (* 0).

Шаг 3. к = 3, поскольку с,₃ = тах{с₁₂, с₁₃, с_и) = тах{20, 30, 10} = 30. Назна­чаем а₃ = с₁₃ = 30 и помечаем узел 3 меткой [30, 1]. Полагаем ;' = 3 и возвращаемся к шагу 2.

Шаг 4. £,= {4,5}.

Шаг 5. к = 5 и а_ь = с₃₅ = тах{10, 20} = 20. Помечаем узел 5 меткой [20, 3]. Получен сквозной путь. Переходим к шагу 5.

Шаг 6. Сквозной путь определяем по меткам, начиная с узла 5 и заканчи­вая узлом 1: (5) -> [20, 3] -> (3) -> [30, 1] -> (1). Таким образом, N, = {1, 3, 5} и /, = min{fl,, а₃, я₅} = {оо, 30, 20} = 20. Вычисляем остаточ­ные пропускные способности вдоль пути /V,:

(с,,, с„) = (30 - 20, 0 + 20) = (10, 20),

(с„, с₅₃) = (20 - 20, 0 + 20) = (0, 20).

Итерация 2

Шаг 1. Назначаем я, = оо и помечаем узел 1 меткой [оо, —]. Полагаем = 1. Шаг 2. £,= {2,3,4}.

Шаг 3. к =2, назначаем а₂ = с,₂ = тах{20, 10, 10} = 20 и помечаем узел 2 меткой [20, 1]. Полагаем i = 2 и возвращаемся к шагу 2.

Шаг 2. £₂={3, 5}.

Шаг 3. к = 3 и а₃ = с₂₃ = 40. Помечаем узел 3 меткой [40, 2]. Полагаем /' = 3 и возвращаемся к шагу 2.

Глава 6. Сетевые модели

[Ю, 3]

д)/₅ = 10 е) Сквозных путей нет

Рис. 6.31. Последовательное выполнение алгоритма нахождения максимального потока

Шаг 2. S₃ = {4} (отметим, что с₃₅ = 0, поэтому узел 5 не включается в S₃).

Шаг 3. k = 4, назначаем я₄ = с₃₄ = 10 и помечаем узел 4 меткой [10, 3]. По­лагаем /' = 4 и возвращаемся к шагу 2.

Шаг 2. ШагЗ.

S_t = {5} (поскольку узлы 1 и 3 уже помечены, они не включаются в 5₄).

к — 5 и а_& = с₄₅ = 20. Помечаем узел 5 меткой [20, 4]. Получен сквозной путь. Переходим к шагу 5.

6.4. Задача о максимальном потоке

Шаг 5. N₂ = {1, 2, 3, 4, 5} и/₂ = min{oo, 20, 40,10, 20} = 10. Вычисляем оста­точные пропускные способности вдоль пути N₂:

(с„, с₂₁) - (20 - 10, 0 + 10) = (10, 10),

(с_я, с₃₂) = (40 - 10, 0 + 10) = (30, 10),

(c_M,cJ-(10-10, 5+ 10)-(0,15),

(с_4б, cj = (20 - 10, 0 + 10) - (10, 10).

Итерация 3

Шаг1.	Назначаем а, = со и помечаем узел 1 меткой [со, —]. Полагаем i = 1.
Шаг 2.	5, = {2, 3,4}.
ШагЗ.	к =2, назначаем а2 = cl2 = шах{10, 10, 10} = 10 и помечаем узел 2
	меткой [10, 1]. Полагаем /' = 2 и возвращаемся к шагу 2.
Шаг 2.	52={3,5}.
ШагЗ.	^=3ия, = св = 30. Помечаем узел 3 меткой [30, 2]. Полагаем i = 3
	и возвращаемся к шагу 2.
Шаг 2.	Sa = 0 (поскольку с34 = с35 = 0). Переходим к шагу 4.
Шаг 4.	Метка [30, 2] узла 3 показывает номер предшествующего узла г-2.
	На этой итерации узел 3 в дальнейшем во внимание не принимается,
	его метку вычеркиваем. Полагаем /' = г = 2 и возвращаемся к шагу 2.
Шаг 2.	St = {5} (поскольку узел 3 удален из возможного сквозного пути).
Шаг 3.	к = 5 и а5 = с25 = 30. Помечаем узел 5 меткой [30, 2]. Получен
	сквозной путь. Переходим к шагу 5.
Шаг 5.	N3 = {1, 2, 5} и/3 = min{co, 10, 30} = 10. Вычисляем остаточные про-
	пускные способности вдоль пути N3:
	(с12, с21) - (10 - 10, 10 + 10) = (0, 20),
	c«) = («О " 10, 0 + 10) = (20, 10).

Итерация 4. На этой итерации получен путь N₄ = {1, 3, 2, 5} сУ, = 10 (проверьте!).

Итерация 5. На этой итерации получен путь N_s = {1, 4, 5} с/₅ = 10 (проверьте!).

Итерация 6. Новые сквозные пути невозможны, поскольку все ребра, исходящие из узла 1, имеют нулевые остаточные пропускные способности. Переходим к ша­гу 6 для определения решения.

Шаг6. Максимальный объем потока в сети равен F = /, +/₂ + ... +/₅ = 20 + 10 + 10 + 10 + 10 = 60 единиц. Значения потоков по различным ребрам вычисляются путем вычитания последних значений оста­

Глава 6. Сетевые модели

точных пропускных способностей (т.е. (с_|/( с.₍)₆) из первоначальных значений пропускных способностей (С,_у,С). Результаты вычисле­ний приведены в следующей таблице.

Ребро {С^,С_р) - (с,у, Су,)₆ Величина потока Направление

(1.2)	(20, 0) - (0, 20) = (20, -20)		1 ->2
(1.3)	(30, 0) - (0, 30) = (30, -30)		1 ->3
(1,4)	(10, 0)-(0, 10) = (10, -10)		1 ->4
(2, 3)	(40, 0) - (40, 0) = (0, 0)		—
(2, 5)	(30, 0) - (10, 20) = (20,-20)		2->5
(3, 4)	(10, 5)-(0, 15) = (10, -10)		3->4
(3, 5)	(20, 0) - (0, 20) = (20, -20)		3->5
(4, 5)	(20, 0) - (0, 20) = (20, -20)		4->5

Программа TORA позволяет найти максимальный поток или в автоматическом режиме, или последовательно — так, как показано ранее. В меню SOLVE/MODIFY выберите команду Solve problem. После задания выходного формата перейдите в выходное окно и выберите команду Maximum Flows (Максимальный поток) или Iterations. На рис. 6.32 показано выходное окно TORA с первыми двумя итерациями решения задачи из примера 6.4.2 (файл ch6ToraMaxFlowEx6-4-2.txt).

УПРАЖНЕНИЯ 6.4.2

1. В задаче из примера 6.4.2

a) для всех ребер определите величины неиспользованных пропускных спо­собностей;

b) найдите величину потока, проходящего через узлы 2, 3 и 4;

c) можно ли увеличить максимальный поток в сети путем повышения про­пускных спесобностей в направлениях 3 -> 5 и 4 —> 5?

2. Найдите максимальный поток и значения потоков, проходящих через каж­дое ребро сети, показанной на рис. 6.33.

3. Три нефтеперегонных завода транспортируют свою продукцию двум распредели­тельным терминалам по сети трубопроводов, которая включает и насосные стан­ции (рис. 6.34). Направления потоков в сети показаны стрелками, пропускные способности отдельных сегментов сети указаны в миллионах баррелей в день.

a) Определите ежедневную производительность каждого нефтеперегонного завода, соответствующую максимальной пропускной способности сети трубопроводов.

b) Определите ежедневную потребность каждого распределительного терми­нала, соответствующую максимальной пропускной способности сети тру­бопроводов.

c) Определите ежедневную пропускную способность каждой насосной стан­ции, соответствующую максимальной пропускной способности сети тру­бопроводов.

6.4. Задача о максимальном потоке

Нефте-

Рис. 6.33. Сеть для задачи упражнения 2 _{рцс g м Сеть дм задачи упражнения 3}

4. Пусть в сети из предыдущего упражнения (рис. 6.34) пропускная способность насосной станции 6 ограничена 60 миллионами баррелей в день. Найдите максимальную пропускную способность сети с учетом этого ограничения.

5. Зерно из трех зернохранилищ доставляется на грузовиках четырем пти­цеводческим фермам, при этом некоторые зернохранилища не могут

Глава 6. Сетевые модели

непосредственно поставлять зерно определенным фермам. Пропускная способность маршрутов от зернохранилищ до птицеводческих ферм огра­ничена количеством используемых грузовиков и числом выполняемых ежедневно рейсов. В следующей таблице показаны ежедневные предло­жения зернохранилищ и ежедневный спрос птицеводческих ферм (в ты­сячах фунтов), в ячейках таблицы указаны пропускные способности соот­ветствующих маршрутов.

Зернохранилища

Фермы

20 20 200

a) Найдите схему транспортировки зерна, обеспечивающую максимальный спрос птицеводческих ферм.

b) Существует ли при данных условиях схема транспортировки, обеспечи­вающая весь спрос птицеводческих ферм?

6. Пусть в задаче из предыдущего упражнения возможна транспортировка зер­на между зернохранилищами 1 и 2, а также 2 и 3. Кроме того, возможна транспортировка между фермами 1 и 2, 2 и 3, 3 и 4. Максимальная пропуск­ная способность в обоих направлениях указанных маршрутов составляет 50 тысяч фунтов. Как данные предположения скажутся на обеспечении пока неудовлетворенного спроса птицеводческих ферм?

7. Родители имеют пять детей подросткового возраста, которых ежедневно привлекают к пяти видам домашней работы. Опыт трудового воспитания де­тей показал, что принудительное (силовое) назначение на работу чревато конфликтами. Поэтому дети сами составили список своих предпочтений, ко­торый приведен в следующей таблице.

Ребенок "* Предпочтительные работы

Ральф 3, 4 или 5

Мэй 1

Бен 1 или 2

Ким 1,2 или 5

Кен 2

Теперь родителям осталось найти такое распределение работ, которое в наи­большей степени учитывало бы предпочтения детей. Найдите максимальное количество таких распределений работ.

8. Четыре фабрики получают заказ на производство четырех типов игру­шек. В следующей таблице показано, какие игрушки должна произво­дить каждая фабрика.

6.4. Задача о максимальном потоке

Фабрика	Тип игрушки
	1,2,3
	2,3
	1.4
	3,4

Ежедневные производственные возможности фабрик составляют 250, 180, 300 и 100 штук игрушек соответственно. Ежедневный спрос на игрушки че­тырех типов составляет 200, 150, 350 и 100 штук. Разработайте производст­венный план, максимально удовлетворяющий спрос на игрушки.

9. Студенческий совет университета рассматривает представления на шесть студентов, являющихся членами четырех студенческих обществ. Студен­ческий совет имеет три секции: естественных, гуманитарных и инженер­ных наук. Совет может принять не более двух студентов в каждую секцию. В следующей таблице показано членство студентов в каждом из четырех студенческих обществ.

Общество	Студент
	1,2,3
	1,3,5
	3,4, 5
	1,2, 4,6

Приведем также распределение студентов по возможному принятию их в различные секции совета.

Секция Студент

естественных наук 1,2,4 гуманитарных наук 3,4

инженерных наук 4, 5, 6

Каждый студент может быть принят только в одну секцию. Могут ли быть представлены в совете все четыре студенческих общества?

10. Максимальный и минимальный потоки в сети с нижними границами про­пускных способностей. В этом разделе во время поиска максимального по­тока в сети неявно предполагалось, что нижние границы пропускных спо­собностей всех ребер равны нулю. В некоторых задачах нижние границы пропускных способностей могут быть строго положительными. В таком слу­чае возникает интерес к вычислению как максимального, так и минимально­го потоков в сети (см. комплексную задачу 6.3 в конце главы). Наличие по­ложительных нижних границ пропускных способностей вызывает определенные затруднения, так как в этом случае сеть вообще может не иметь допустимого потока. Максимальный и минимальный потоки в сети можно найти, выполняя следующие действия.

Шаг 1. Найдите начальное допустимое решение для сети с положитель­ными нижними границами пропускных способностей.

Глава 6. Сетевые модели

Шаг 2. Используя допустимое решение, найденное на первом этапе, опре­делите максимальный и минимальный потоки в сети.

a) Покажите, что поток через дугу (i, j), величина которого огра­ничена неравенствами 1_Ц < х_ц < и_ц, можно представить в виде стока со спросом J. в узле i, источником с предложением l_if в уз­ле j и потоком, ограниченным неравенствами 0 < x'_tj < и_ц - 1_Ц.

b) Покажите, что нахождение допустимого решения в исходной сети эквивалентно нахождению максимального потока в сети, где 1) поток х через каждую дугу (£, заменен потоком х'- с ог­раничениями 0 < х'д < и_ц - l,j (как показано в предыдущем пунк­те); 2) все источники "слиты" в один с выходящей из него ду­гой, имеющей пропускную способность I ; 3) все стоки "слиты" в один с входящей в него дугой, имеющей пропускную способ­ность /,.; 4) конечный узел t соединен с узлом источника s ис­ходной сети дугой с бесконечной пропускной способностью. Допустимое решение существует, если максимальный поток в новой сети равен сумме нижних границ пропускных способ­ностей исходной сети. Примените описанную процедуру к сле­дующей сети и найдите допустимое решение (поток).

С/у. Щ)

(5, 20) (0, 15) (4, 10) (3, 15) (0, 20)

Дуга (/,./)

(1,2) (1,3) (2, 3) (2, 4) (3, 4)

c) Чтобы вычислить минимальный поток в исходной сети, ис­пользуйте допустимое решение, найденное в предыдущем пункте, совместно с алгоритмом поиска максимального пото­ку. (Совет. Сначала на основе имеющегося допустимого реше­ния найдите остаточную сеть. Далее определите максимальный поток от конечного узла сети к начальному. Теперь, комбини­руя допустимый и максимальный потоки, найдите минималь­ный поток в исходной сети.)

d) Используя алгоритм нахождения максимального потока с до­пустимым решением, найденным в п. Ь, определите макси­мальный поток в исходной сети. (Совет. Начните с определе­ния остаточной сети. Далее примените алгоритм поиска сквозных путей к этой сети.)

6.4.3. Формализация задачи поиска максимального потока как задачи ЛП

Обозначим через * . величину потока, проходящего по дуге (£, j), пусть с,. — про­пускная способность этой же дуги. Предположим, что необходимо найти макси­мальный поток между начальным узлом s и конечным узлом t.

6.4. Задача о максимальном потоке

Ограничениями задачи ЛП будут уравнения баланса входного и выходного по­токов для каждого узла. Целевая функция максимизирует или величину общего потока, "выходящего" из начального узла, или величину общего потока, "входящего" в конечный узел.

Пример 6.4.3

В задаче вычисления максимального потока в сети, показанной на рис. 6.29 (пример 6.4.2), s=l и f=5. В следующей таблице приведена соответствующая за­дача ЛП с двумя различными целевыми функциями, одна из которых максимизи­рует поток, выходящий из узла 1 (функция z_t), вторая максимизирует поток, вхо­дящий в узел 5 (функция г_г).

Х12	*13		Х23	Х25	Х34	Х35	Х43	Х45
Максимизировать Zi 1 Максимизировать z2
Узел 2 1 УзелЗ Узел 4			-1 1	-1	-1 1	-1	-1	II II II ООО
Пропускная способность 20
Оптимальное решение этой задачи ЛП с использованием любой целевой функции составляют х1г = 20, хп = 30, х14=10, х2Ъ = 20, х34=10, хзъ = 20, xi5 = 2Q. Макси­мальный поток равен г2 = 60.

УПРАЖНЕНИЯ 6.4.3

1. Решите задачу из упражнения 6.4.2.2 как задачу линейного программирования.

2. Решите задачу из упражнения 6.4.2.5 как задачу линейного программирования.

6.4.4. Решение задачи определения максимального потока в Excel

Шаблон Excel, предназначенный для решения общей транспортной задачи (см. раздел 5.3.3), можно немного модифицировать, чтобы найти максимальный поток. Максимальный размер сети — 10 узлов. На рис. 6.35 показан рабочий лист, на котором решается задача из примера 6.4.2 (файл ch6SolverMaxFlow.xls). Мат­рица пропускных способностей записана в диапазоне В6:К15.⁴ Незаполненные ячейки матрицы пропускных способностей показывают, что соответствующие дуги имеют бесконечную пропускную способность. Нулевое значение пропускных спо­собностей вводится для несуществующих дуг.

После того как будут введены значения пропускных способностей, рабочий лист пе-ресчитывается автоматически. Выделенные столбцы В, С, F и G содержат исходные данные задачи, необходимые для использования средства Поиск решения. Диапа­зон В20:В39 (изменяемые ячейки для средства Поиск решения) содержит величины по­токов, проходящие по каждой дуге. Столбец С содержит значение пропускных способ­

⁴ На рис. 6.35 строки от 11 до 16 скрыты для экономии места.

Главв 6. Сетевые модели

ностей дуг (диапазон С20:С39). Все эти вычисления выполняются автоматически. Все, что необходимо сделать вам для решения задачи, — это указать диапазон изменяемых ячеек и задать ограничения в диалоговом окне средства Поиск решения. На рис. 6.35 видно, что изменяемые ячейки составляют диапазон В20:В39, а ограничения задают­ся как F20:F22=G20:G22 (баланс потоков для узлов 2, 3 и 4) и В20:В39<=С20:С39 (ограничения пропускных способностей дуг). Отметим, что целевая ячейка устанав­ливается автоматически и ее не надо изменять. Следует установить переключатель Равной максимальному значению, поскольку решается задача максимизации.