Методы регрессионного анализа
Методы регрессионного анализа
Сущность и задачи регрессионного анализа
В дальнейшем будем рассматривать две модели регрессионного анализа (РА). Модель 1. В данной модели зависимая переменная – случайная величина, а… Модель 2. В данной модели как зависимая переменная, так и независимые переменные являются случайными величинами.…Однофакторный регрессионный анализ
Модели однофакторного регрессионного комплекса
, соответственно. Данные модели могут быть представлены в несколько иной форме, а именно:Построение уравнения регрессии
y = f(x). (9.2.6) Эта функция определяется также и вектором числовых параметров (a0, a1,…, ak)т = A<k+1>. (9.2.7)Проверка адекватности уравнения регрессии
Адекватность уравнения определяется, прежде всего, правильным выбором класса Y функций регрессии. Для проверки соответствия выбранного класса функций регрессии опытным данным… , . (9.2.21)Проверка значимости коэффициентов регрессии
H0j: aj ¹ 0, при соответствующих конкурирующих гипотезах H1j: aj = 0. В качестве показателя согласованности при проверке гипотез H0j используется выражениеПримеры однофакторного регрессионного анализа
Из вышеизложенного следует, что однофакторный регрессионный анализ проводится в следующей последовательности.
1. Выбирается вид функции регрессии.
2. Составляется система нормальных уравнений.
3. Находится решение системы нормальных уравнений (определяются оценки коэффициентов регрессии).
4. Проверяется адекватность построенного уравнения регрессии экспериментальным данным.
5. Проверяется значимость коэффициентов регрессии.
6. Повторно проверяется адекватность уравнения регрессии после исключения незначимых коэффициентов.
П р и м е р 9.1. Для исследования зависимости выходного сигнала y системы от входного воздействия x проведены испытания, результаты которых сведены в табл.9.3.
Необходимо построить уравнение регрессии y = f(x) в предположении, что оно является алгебраическим полиномом третьей степени. Расчёты произвести в скалярной форме.
Таблица 9.3
Массив экспериментальных данных
| x | –2 | –1 | |||
| y | –39 |
▼ 1. Класс функций Y задан в условии задачи – это полиномы третьей степени
y = a0x3 + a1x2 + a2x + a3. (9.2.31)
Они являются функциями вида (9.2.11). Для данного случая выражение (9.2.11) представляется как
y = a0 f0(x) + a1 f1(x) + a2 f2(x) + a3 f3(x), (9.2.32)
где f0(x) = x3, f1(x) = x2, f2(x) = x, f3(x) = 1. (9.2.33)
2. Для функции (9.2.32) и заданного количества опытов система нормальных уравнений (9.2.17) принимает вид
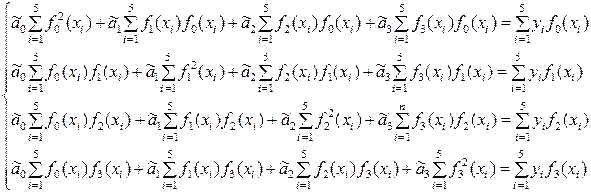
(9.2.34)
С учётом (9.2.33) система уравнений (9.2.34) преобразуется следующим образом:
 (9.2.35)
(9.2.35)
3. Оценки коэффициентов уравнения регрессии (т.е. решение системы линейных уравнений (9.2.35)) находим по формулам (9.2.18):
 . (9.2.36)
. (9.2.36)
Развёрнутый вид определителей в соотношениях (9.2.36):
 ;
; 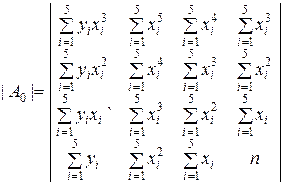 ;
;
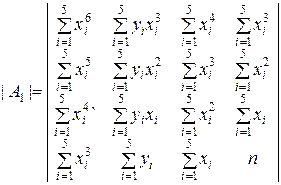 ;
;  ;
;
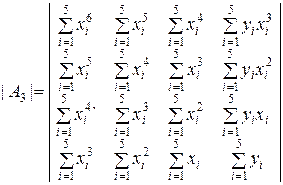 .
.
Составляем расчётную таблицу 9.4 для вычисления коэффициентов системы линейных уравнений (9.2.35).
Таблица 9.4
Расчётная таблица
| xi | yi | 
| 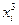
| 
| 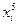
| 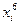
| 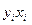
| 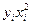
| 
|
| –2 | –8 | –32 | –10 | –40 | |||||
| –1 | –1 | –1 | –4 | –4 | |||||
| –39 | –117 | –351 | –1053 | ||||||
 =
=1 =
=1
| 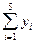 =
= –23 =
= –23
|  =
=15 =
=15
|  =
=19 =
=19
|  =
=99 =
=99
| 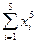 =
=211 =
=211
| 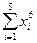 =
=795 =
=795
| 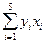 =
= –129 =
= –129
| 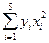 =
= –325 =
= –325
| 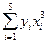 =
= –1095 =
= –1095
|
Получаем систему уравнений (9.2.35) с числовыми значениями коэффициентов при неизвестных:
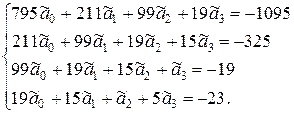
Определитель | A | четвёртого порядка вычисляем разложением по первой строке:
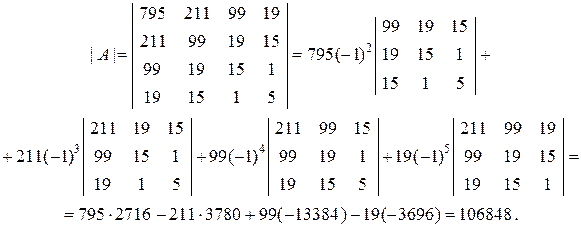
При разложении определителя | A | получены четыре определителя третьего порядка, которые вычисляем также разложением по первой строке:

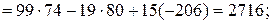
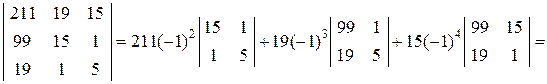
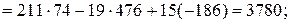
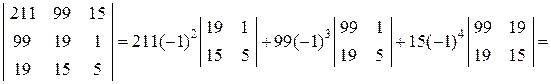

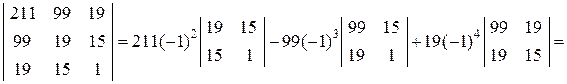

Аналогично находим
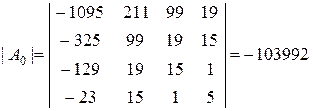 ;
;
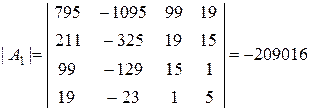 ;
;
 ;
;
 .
.
По формулам (9.2.36) вычисляем оценки коэффициентов регрессии:

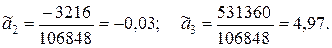
Получили уравнение регрессии
 .
.
4. Проверяем адекватность регрессионной зависимости экспериментальным данным. Для этого необходимо вычислить оценки дисперсий (9.2.25) и (9.2.26). Составляем табл.9.5.
Таблица 9.5
Расчётная таблица
| xi | yi | 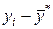
| 
| 
| 
| 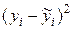
|
| –2 | 9,6 | 92,16 | 4,95 | 0,05 | 0,0025 | |
| –1 | 8,6 | 73,96 | 4,01 | –0,01 | 0,0001 | |
| 9,6 | 92,16 | 4,97 | 0,03 | 0,0009 | ||
| 6,6 | 43,56 | 2,01 | –0,01 | 0,0001 | ||
| –39 | –34,4 | –38,95 | –0,05 | 0,0025 | ||
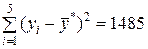
| 
|
Оценка математического ожидания выходной переменной y, которая используется при расчётах в табл.9.5, найдена по формуле (5.1.1):
 .
.
Необходимые данные для вычисления оценок дисперсий s2 и 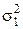 берём из табл.9.5:
берём из табл.9.5:
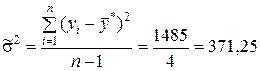 ;
;
 .
.
Наблюдаемое значение показателя согласованности (9.2.23):
 .
.
Критическое значение показателя согласованности при уровне значимости a = 0,01 и степенях свободы f1 = n – 1 = 4, f2 = n – k – 1 = 1, находим в приложении 5:
F(0,01; 4; 1) = 5625.
Очевидно, что неравенство (9.2.24) выполняется, т.е. F >F(0,01; 4; 1). Следовательно, нулевая гипотеза H0 о соответствии функции регрессии вида (9.2.31) экспериментальным данным принимается.
5. Проверяем значимость коэффициентов уравнения регрессии.
Для вычисления наблюдаемых значений показателя согласованности (9.2.30) необходимо найти диагональные элементы корреляционной матрицы (9.2.28). В рассматриваемом примере матрица F представляется следующим образом:
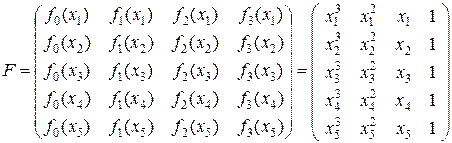 . (9.2.37)
. (9.2.37)
Находим произведение транспонированной матрицы F на исходную:

 (9.2.38)
(9.2.38)
Далее требуется найти элементы главной диагонали матрицы  :
:
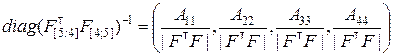 ,
,
где 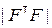 – определитель матрицы
– определитель матрицы 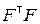 ; Aii,
; Aii, 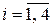 – алгебраические дополнения элементов главной диагонали этой же матрицы.
– алгебраические дополнения элементов главной диагонали этой же матрицы.
Вычисляем определитель и алгебраические дополнения:
 ;
;

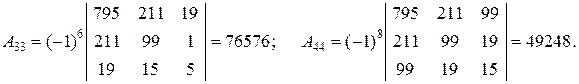
Таким образом, имеем
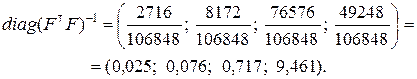
Главная диагональ (9.2.29) корреляционной матрицы вектора оценок коэффициентов регрессии:

 .
.
Вычисляем оценки средних квадратических отклонений коэффициентов  ,
,  :
:
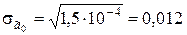 ;
; 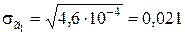 ;
;
 ;
;  .
.
Находим наблюдаемые значения показателя (9.2.27):
 .
.
Критическое значение показателя согласованности при уровне значимости a = 0,01 и одной степени свободы f = 1 находим в приложении 6: t(0,01; 1) = 63,7.
Проверяем условие (9.2.30) и получаем:
t0 > t(0,01; 1); t1 > t(0,01; 1); t2 < t(0,01; 1); t3 > t(0,01; 1).
На основе приведённых неравенств делаем вывод, что коэффициенты a0, a1 и a3 являются значимыми, а коэффициент a2 принимаем равным нулю.
Окончательный вид уравнения регрессии
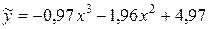 .
.
6. Проверяем адекватность последнего уравнения по критерию Фишера. Составляем табл.9.6.
Таблица 9.6
Расчётная таблица
| xi | yi | 
| 
| 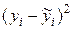
|
| –2 | 4,89 | 0,11 | 0,0121 | |
| –1 | 3,98 | 0,02 | 0,0004 | |
| 4,97 | 0,03 | 0,0009 | ||
| 2,04 | –0,04 | 0,0016 | ||
| –39 | –38,86 | –0,14 | 0,0196 | |
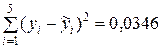
|
Вычисляем оценку остаточной дисперсии с учётом результата, полученного в табл.9.6:
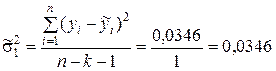 .
.
Общая дисперсия остаётся прежней. Поэтому наблюдаемое значение показателя согласованности (9.2.33) будет следующим:
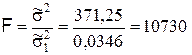 .
.
Очевидно, что при критическом значении показателя согласованности F(0,01; 4; 1) = 5625 неравенство (9.2.24) выполняется. Таким образом, повторная проверка адекватности по критерию Фишера подтверждает справедливость гипотезы о соответствии функции регрессии вида (9.2.31) экспериментальным данным.
▲
П р и м е р 9.2. В условиях примера 9.1 построить уравнение регрессии, но расчёты произвести в матричной форме.
▼ Матричное уравнение (9.2.19) для рассматриваемого примера имеет вид
 , (9.2.39)
, (9.2.39)
где матрицы F и  представлены выражениями (9.2.37), (9.2.38) соответственно;
представлены выражениями (9.2.37), (9.2.38) соответственно;
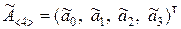 ;
; 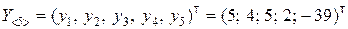 .
.
Выражение (9.2.20) для вычисления оценок коэффициентов регрессии представляется в виде
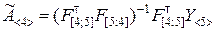 . (9.2.40)
. (9.2.40)
Вычисляем обратную матрицу  для матрицы
для матрицы
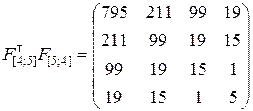 .
.
Алгебраические дополнения элементов матрицы 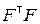 :
:
A11 = 2716; A21 = –3780; A31 = –13384; A41 = 3696;
A12 = –3780; A22 = 8172; A32 = 15480; A42 = –13248;
A13 = –13384; A23 = 126304; A33 = 76576; A43 = –10896;
A14 = 3696; A24 = –13248; A34 = –10896; A44 = 49248.
Определитель указанной матрицы |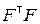 | = 106848.
| = 106848.
В результате получили обратную матрицу

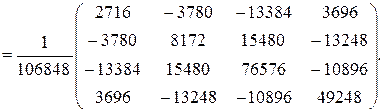
Далее вычисляем матрицу в правой части уравнения (9.2.39):
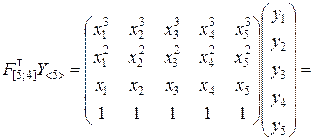
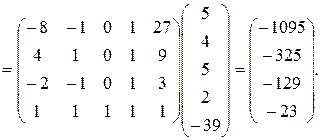
По формуле (9.2.40) находим оценки коэффициентов регрессии
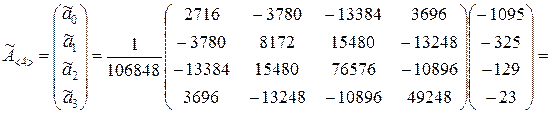

Так же, как и в примере 9.1 при расчётах в скалярной форме, получили уравнение регрессии
 .
.
Проверка адекватности уравнения экспериментальным данным и значимость коэффициентов регрессии выполняется аналогично тому, как это сделано в примере 9.1.
▲
Многофакторный линейный регрессионный анализ
Модели многофакторного линейного регрессионного анализа
В настоящем подпараграфе рассмотрим модели многофакторного (множественного) регрессионного анализа, являющиеся линейными как относительно… Модель РА-1 определяется выражением , (9.3.1)Построение уравнения множественной регрессии
(9.3.3) в выражении . (9.3.4)Проверка адекватности уравнения множественной регрессии
, (9.3.17) где – оценка общей дисперсии наблюдаемой переменной; – оценка остаточной… Оценки дисперсий, входящих в соотношение (9.3.17), определяются по формуламСелекция факторов
Следуя представленной в указанном подпараграфе схеме, необходимо проверить нулевые гипотезы о неравенстве нулю коэффициентов bj: H0j: bj ¹ 0, . Конкурирующие гипотезы состоят в предположении о равенстве нулю коэффициентов:Пример многофакторного линейного регрессионного анализа
Из вышеизложенного очевидно, что многофакторный линейный регрессионный анализ проводится в следующей последовательности.
1. Определяется количество слагаемых в линейной функции регрессии вида (9.3.1) или (9.3.2) в зависимости от числа факторов.
2. Выполняется центрирование факторов.
3. Составляется система нормальных уравнений.
4. Находится решение системы нормальных уравнений (определяются оценки коэффициентов регрессии).
5. Проверяется адекватность построенного уравнения регрессии экспериментальным данным.
6. Производится селекция факторов.
7. Повторно проверяется адекватность уравнения регрессии после исключения незначимых факторов.
П р и м е р 9.3. Для исследования зависимости выходного сигнала y системы от входного воздействия X<2> = (x1, x2)т, проведены испытания, результаты которых сведены в табл.9.9.
Необходимо построить регрессионную зависимость y от X<2> в предположении, что она является линейным алгебраическим полиномом.
Таблица 9.9
Массив экспериментальных данных
| x1 | –0,5 | 0,8 | 0,4 | 0,5 | 0,6 | |
| x2 | –3 | –1 | 0,5 | 1,5 | ||
| y | –15,1 | –1 | 19,9 | 9,5 | 16,5 | 47,9 |
▼ 1. В рассматриваемой задаче функция регрессии представляет собой линейный алгебраический полином от двух независимых переменных
y = b0 + b1x1 + b2x2.
2. Составляем таблицу экспериментальных данных с центрированными значениями факторов.
Предварительно вычисляем средние значения факторов:
 ;
;
 ;
;
Используя формулы (9.3.5), производим центрирование факторов, результаты заносятся в таб.9.10.
Таблица 9.10
Массив экспериментальных данных с центрированными значениями факторов
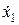
| –0,8 | –0,3 | 0,5 | 0,1 | 0,2 | 0,3 |
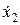
| –4 | –2 | –0,5 | 0,5 | ||
| y | –15,1 | –1 | 19,9 | 9,5 | 16,5 | 47,9 |
Таким образом, вначале коэффициенты регрессии оцениваем в выражении функции (9.3.7), которая для данной задачи принимает вид
 (9.3.24)
(9.3.24)
3. Система нормальных уравнений представляется следующим образом:
 (9.3.25)
(9.3.25)
4. Представим и решим систему (9.3.25) в матричной форме.
Матричное уравнение, эквивалентное данной системе, принимает вид
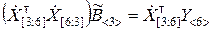 , (9.3.26)
, (9.3.26)
где  ;
;
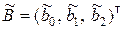 ;
; 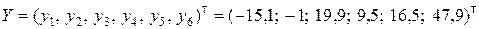 .
.
Выражение (9.3.16) для вычисления оценок коэффициентов регрессии представляется равенством
 . (9.3.27)
. (9.3.27)
Вычисляем матрицу  :
:
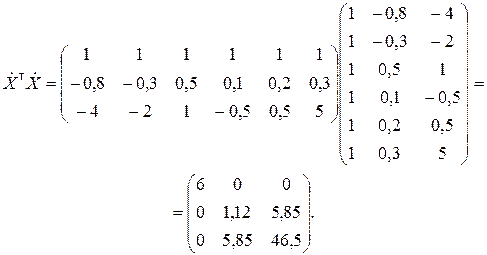
Для полученной матрицы находим обратную матрицу:
 (9.3.28)
(9.3.28)
Далее находим матрицу в правой части уравнения (9.3.26):

По формуле (9.3.27) вычисляем оценку вектора коэффициентов регрессии
 .
.
Получим следующее уравнение регрессии:
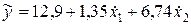 . (9.3.29)
. (9.3.29)
5. Проверяем адекватность уравнения (9.3.29) экспериментальным данным.
Предварительно вычисляем оценки дисперсий (9.3.18) и (9.3.19). Для этого составляем табл.9.11.
Таблица 9.11
Расчётная таблица
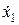
| 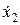
| yi | 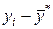
| 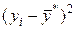
| 
| 
| 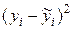
|
| –0,8 | –4 | –15,1 | –28 | –15,2 | 0,01 | 0,0001 | |
| –0,3 | –2 | –1 | –13,9 | –0,98 | –0,02 | 0,0004 | |
| 0,5 | 19,9 | 20,3 | –0,40 | 0,16 | |||
| 0,1 | –0,5 | 9,5 | –3,4 | 11,6 | 9,66 | 0,16 | 0,0256 |
| 0,2 | 0,5 | 16,5 | 3,6 | 16,6 | –0,10 | 0,01 | |
| 0,3 | 47,9 | 0,90 | 0,81 | ||||
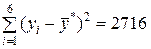
| 
|
Оценка математического ожидания выходной переменной y, используемая при расчётах в табл.9.11, найдена по формуле (5.1.1):
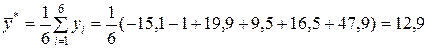 .
.
Необходимые данные для вычисления оценок дисперсий берём из табл.9.11:
 ,
,
 , (9.3.30)
, (9.3.30)
Наблюдаемое значение показателя согласованности (9.3.17):

Для отыскания критического значения показателя согласованности при уровне значимости a = 0,01 и степенях свободы f1 = n – 1 = 5, f2 = n – k – 1 = 3 используем приложение 5 и получаем F(0,01;5;3) = 28,24.
Поскольку неравенство (9.3.20) выполняется (F > F(0,01;5;3)), нулевую гипотезу об адекватности функции регрессии вида (9.3.24) экспериментальным данным принимаем.
6. Выполняем селекцию факторов. Для этого находим элементы главной диагонали корреляционной матрицы (9.3.22). Учитывая выражения (9.3.28) и (9.3.30), имеем
 .
.
Оценки средних квадратических отклонений коэффициентов 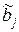 ,
, 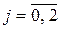 принимают значения:
принимают значения:
 ;
; 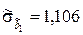 ;
;  .
.
Для каждого фактора находим наблюдаемое значение показателя согласованности (9.3.21):
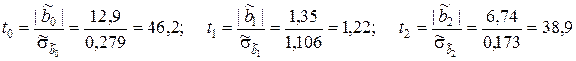 .
.
Для числа степеней свободы f = n – k –1 = 3 и уровня значимости a = 0,01 критическое значение показателя согласованности t(0,01;3) = 5,84. Следовательно,
t0 > t(0,01;3), t1 < t(0,01;3), t3 > t(0,01;3).
В отношении фактора 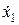 принимаем конкурирующую гипотезу о его незначимости. Тогда в правой части выражения (9.3.24) второе слагаемое приравниваем к нулю. Поскольку в исходной матрице
принимаем конкурирующую гипотезу о его незначимости. Тогда в правой части выражения (9.3.24) второе слагаемое приравниваем к нулю. Поскольку в исходной матрице 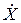 исключается второй столбец, оценки коэффициентов регрессии b0 и b2 необходимо пересчитать.
исключается второй столбец, оценки коэффициентов регрессии b0 и b2 необходимо пересчитать.
Пересчёт выполняем в том же порядке, который приведён выше (сохраняем ту же нумерацию пунктов).
1. Функция регрессии в данном случае представляет собой линейный алгебраический полином от одной независимой переменной
y = b0 + b2x2. (9.3.31)
2. Составляем табл.9.12 экспериментальных данных с центрированными значениями фактора x2.
Таблица 9.12
Массив экспериментальных данных с центрированными значениями фактора
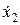
| –4 | –2 | –0,5 | 0,5 | ||
| y | –15,1 | –1 | 19,9 | 9,5 | 16,5 | 47,9 |
Коэффициенты регрессии предварительно оцениваем в уравнении
 . (9.3.32)
. (9.3.32)
3. Система нормальных уравнений принимает вид
 (9.3.33)
(9.3.33)
4. Матричное уравнение, эквивалентное системе (9.3.33), представляется как
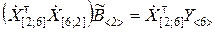 , (9.3.34)
, (9.3.34)
где
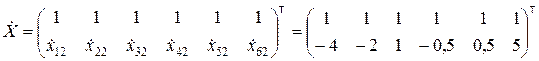 ;
;
 ;
;
 .
.
Оценки коэффициентов регрессии определяются равенством
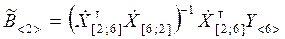 . (9.3.35)
. (9.3.35)
Вычисляем матрицу  :
:
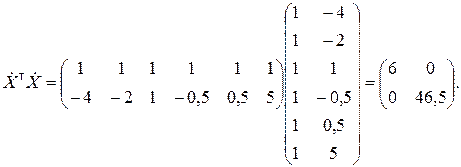
Находим обратную матрицу:
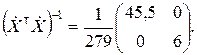 .
.
Матрица в правой части уравнения (9.3.33) есть не что иное, как вектор-столбец с двумя компонентами:

Оценку вектора коэффициентов регрессии находим по формуле (9.3.35):
 .
.
Получим уравнение регрессии с одним фактором
 . (9.3.36)
. (9.3.36)
5. Проверяем адекватность уравнения (9.3.36) экспериментальным данным.
Для вычисления оценки дисперсии (9.3.19) составляем расчётную табл.9.13. Оценка дисперсии (9.3.18) остаётся прежней.
Таблица 9.13
Расчётная таблица

| yi | 
| 
| 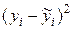
|
| –4 | –15,1 | –14,7 | –0,4 | 0,16 |
| –2 | –1 | –0,9 | –0,1 | 0,01 |
| 19,9 | 19,8 | 0,1 | 0,01 | |
| –0,5 | 9,5 | 9,4 | 0,1 | 0,01 |
| 0,5 | 16,5 | 16,3 | 0,2 | 0,04 |
| 47,9 | 47,4 | 0,5 | 0,25 | |
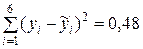
|
Получаем оценку остаточной дисперсии:
 .
.
Показатель согласованности (9.3.17) принимает значение
 .
.
Критическое значение данного показателя при a = 0,01, f1 = n – 1 = 5, f2 = n – k – 1 = 4 составляет F(0,01;5;4) = 15,52. Поскольку имеет место неравенство F > F(0,01;5;4), нулевая гипотеза об адекватности функции регрессии (9.3.31) экспериментальным данным принимается.
6. Выполняем селекцию факторов. Главная диагональ корреляционной матрицы (9.3.22) с учётом выражений (9.3.28) и (9.3.30) принимает вид
 .
.
Из полученного результата следует, что
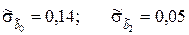 .
.
Наблюдаемые значения показателя согласованности (9.3.21) для факторов  и
и 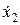 :
:
 .
.
Находим критическое значение данного показателя в приложении 6, оно составляет t(0,01;4) = 4,6. Таким образом,
t0 > t(0,01; 4), t2 > t(0,01;4).
Принимаем нулевую гипотезу о значимости факторов  и
и 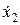 в уравнении (9.3.36).
в уравнении (9.3.36).
Переходим к уравнению вида (9.3.31) с нецентрированными факторами:
 ,
,
т.е.
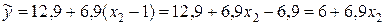
или, окончательно
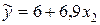 .
.
▲