Доказательство.

Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2=B2B3.
Проведем через точку В2 прямую С1С2, параллельную прямой A1A2. Получаем параллелограммы A1C1BA2 и A2B2C2A3. По свойствам параллелограмма, A1A2 = C1B2 и A2A3 = B2C2. Так как A1A2 = A2A3, то C1B2 = B2C2.
Δ C1B2B1 = Δ C2B2B3 по второму признаку равенства треугольников (C1B2 = B2C2, ∠ C1B2B1 = ∠ C2B2B3, как вертикальные, ∠ B1C1B2 = ∠ = B3C2B2, как внутренние накрест лежащие при прямых B1C1 и C2B3 и секущей С1С2). Из равенства треугольников следует, что B1B2=B2B3. Теорема доказана.

2)
Окружность, вписанная в треугольник.

Окружность называется вписанной в треугольник, если она касается всех его сторон.

[П] Теорема о центре окружности, вписанной в треугольник.

Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

Дано: АВС — данный треугольник; О — центр вписанной в него окружности; D, Е и F — точки касания окружности со сторонами треугольника (рис. 27).

Доказать: О — точка пересечения биссектрис.

Доказательство. Прямоугольные треугольники AOD иАОЕ равны по гипотенузе и катету. У них гипотенуза ОА — общая, а катеты OD и ОЕ равны как радиусы. Из равенства треугольников следует равенство углов OAD и ОАЕ. А это значит, что точка О лежит на биссектрисе треугольника, проведенной из вершины А. Точно так же доказывается, что точка О лежит на двух биссектрисах треугольника.

[А] Теорема об окружности, вписанной в треугольник.

В любой треугольник можно вписать окружность.



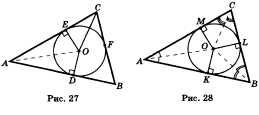
Дано: A ABC — данный треугольник, О — точка пересечения биссектрис, М, L и К — точки касания окружности со сторонами треугольника (рис. 28).

Доказать: О — центр окружности, вписанной в АВС.

Доказательство. Проведем из точки О перпендикуляры OK, OL и ОМ соответственно к сторонам АВ, ВС и СА (см. рис. 28). Так как точка О равноудалена от сторон треугольника ABC, то О К = OL = = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки K L M. Стороны треугольника ABC касаются этой окружности в точках К, L, М, так как они перпендикулярны к радиусам ОК, OL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник ABC. Теорема доказана.

Замечание. Отметим, что в треугольник можно вписать только одну окружность. В самом деле, допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают.

Билет№3.

1. Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

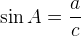
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

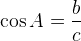
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

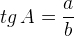
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

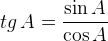
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

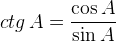
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

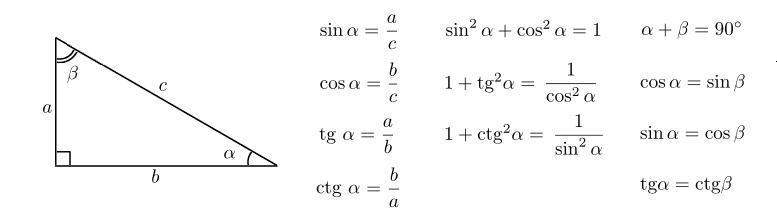
2.
Прямоугольник — это параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны.

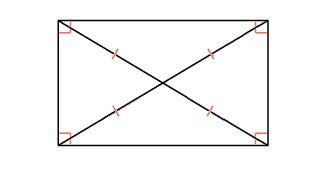Свойства прямоугольника.

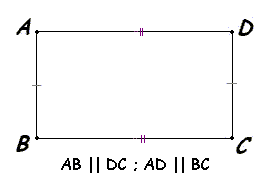
	1. Противолежащие стороны параллельны и равны(как частный случай параллелограмма).
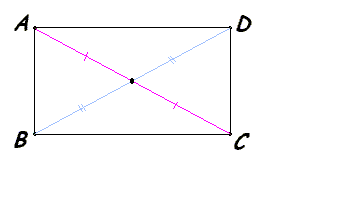
	2. Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам(как частный случай параллелограмма)..
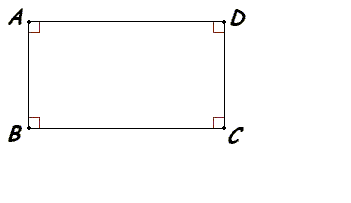
	3. Все углы прямоугольника равны 900 (по определению).
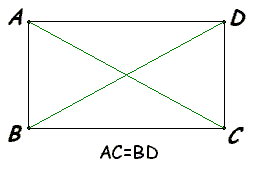
	4. Диагонали прямоугольника равны

Рубрика: «Докажи сам».

Билет№14.

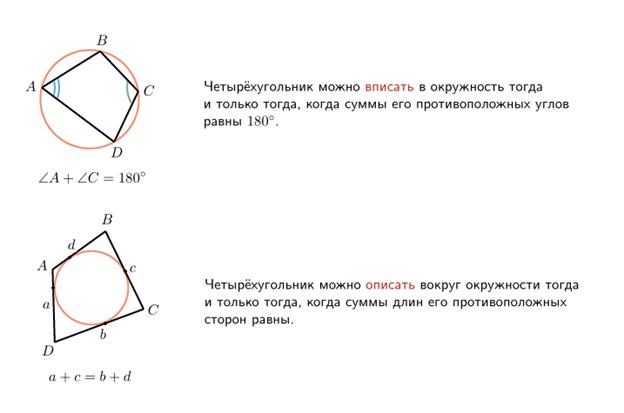
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники.