рефераты конспекты курсовые дипломные лекции шпоры

Раздел Образование
/
Свойства параллелограмма

Реферат Курсовая Конспект

Выберите учебное заведение

Свойства параллелограмма

Свойства параллелограмма - раздел Образование, Центральная и осевая симметрии. Сравнение симметрий. Параллелограмм. Признаки параллелограмма. Теоремы Для Параллелограмма Верно Каждое Из Последующих Утверждений ...

Для параллелограмма верно каждое из последующих утверждений

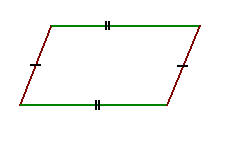
	Противолежащие стороны попарно равны		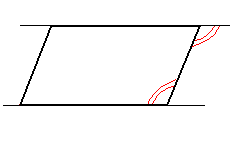Противолежащие стороны попарно параллельны
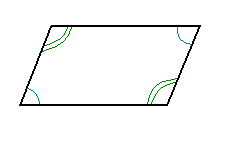
	Противолежащие углы равны		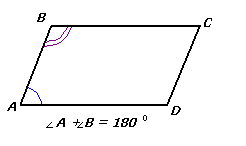Сумма углов, прилежащих к одной стороне, равна 180⁰
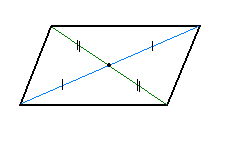
	Диагонали пересекаются и точкой пересечения делятся пополам		Каждая диагональ делит параллелограмм на два равных треугольника

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм.

Доказательство

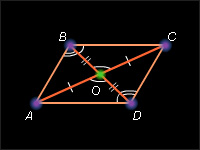
Пусть ABCD – данный четырехугольник. По условию AO = OC, BO = OD. Так как углы (AOB) и (COD) равны как вертикальные, то треугольник AOB равен треугольнику COD, и, следовательно, углы (OAB) и (OCD) равны. Эти углы являются внутренними накрест лежащими при прямых (AB) и (CD) и секущей (AC) и по прямые (AB) и (CD) параллельны. Аналогично из равенства треугольников AOD и COB следует равенство углов (OAD) и (OCB) и по теореме 3.2 – параллельность прямых (AD) и (BC). Из полученных результатов следует, что четырехугольник ABCD – параллелограмм. Теорема доказана.

Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.

Доказательство

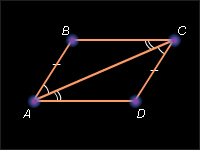
Пусть ABCD – данный четырехугольник и (AB) || (CD), AB = CD.

Рисунок 7.2.2. К теореме 7.2

Проведем диагональ AC. Получившиеся треугольники ABC и ADC равны. Действительно, стороны AB и CD равны по условию, сторона AC – общая, углы ACD и BAC равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей AC. Из равенства треугольников следует равенство углов CAD и ACB. Данные углы являются внутренними накрест лежащими при прямых BC и AD и секущей AC. По теореме 3.2 прямые BC и AD параллельны. Следовательно, четырехугольник ABCD параллелограмм по определению. Теорема доказана.

Билет № 17.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Центральная и осевая симметрии. Сравнение симметрий. Параллелограмм. Признаки параллелограмма. Теоремы

Многоугольник называется выпуклым если он лежит в одной полуплоскости относительно любой прямой содержащей его сторону Сумма углов выпуклого... Центральная и осевая симметрии Центральная... Сравнение симметрий...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свойства параллелограмма

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Центральная симметрия
Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1 (рис.1). Точка О считается симметричной самой себе. Пример центральной с

Осевая симметрия
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему (рис.3). Каждая точка прямой а сч

Пропорциональные отрезки
Отношением отрезков AB и CD называется отношение их длин, то есть . Говорят, что отрезки AB и СD пр

Доказательство.
Пусть ABCD – данный параллелограмм, O – точка пересечения диагоналей данного параллелограмма. Δ AOD = Δ COB по первому признаку равенства треугольников (OD = OB, AO = OC по условию т

Теорема.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.

Доказательство.
Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA. Проведе

Доказательство.
Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A

Теорма о средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Пусть MN — средняя линия треугольника ABC (рис 1). Докажем, что MN || AC и MN = 1/2 AC. Т

Доказательство
Рассмотрим прямоугольник со сторонами a, b и площадью S. Докажем, что S = ab. Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке

Площадь параллелограмма
Одну из параллельных сторон параллелограмма назовем основанием, а отрезок, опущенный из любой точки основания на противолежащую сторону – высотой

Теоремы о касательной к окружности.
Теорема 1. Прямая, перпендикулярная к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности. Пусть ОМ— радиус окружности, СD_|_OМ (черт

Доказательство.
Рассмотрим трапецию ABCD с основаниями AD иBC, выс

Теорема доказана.
Так же площадь трапеции можно найти с помощью следующих формул: 1. S = mh, где m — средняя линия, h — высота трапеции. 2.

Построения, основанные на свойствах прямоугольного треугольника
Задача 2. Даны два отрезка a и b. Постройте отрезок: а) x = ; б) x =

Теорема, обратная теореме Пифагора
Теорема (теорема, обратная теореме Пифагора). Если в треугольнике со сторонами a, b и c выполняется равенство c2 = a 2 + b 2

Доказательство
Рассмотрим пря