Теорма о средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Пусть MN — средняя линия треугольника ABC (рис 1). Докажем, что MN || AC и MN = 1/2 AC.

Треугольники BMN и BAC подобны по второму признаку подобия треугольников (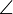B — общий, BM / BA = BN / BC = 1 / 2), поэтому 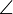1 = 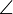2 и MN / AC = 1 / 2. Из равенства 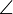1 = 2 следует, что MN || AC, а из второго равенства, что MN = 1 / 2 AC. Теорема доказана.

 

 

Билет№4.

1. Следующая группа углов - это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так... Исторически.) Дальше будет видно, чем хороши эти углы.

Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:

 

Угол х (в градусах)
Угол х (в радианах)
sin x
cos x
tg x					не сущ.
ctg x	не сущ.

 

 

2. Ромб и его свойства

По определению, ромб — это параллелограмм, все стороны которого равны.

Свойства ромба:

· Все свойства параллелограмма.

· Диагонали ромба взаимно перпендикулярны.

· Диагонали ромба являются биссектрисами углов.

· В ромб всегда можно вписать окружность.

 

 

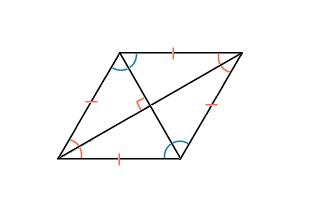
Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.
Доказательство.
Пусть ABCD – данный ромб. Диагонали ромба пересекаются в точке O.
По свойству параллелограмма AO = OC, значит BO – медиана Δ ABC. А так как треугольник ABC - равнобедренный, то по свойствам медианы равнобедренного треугольника проведенной к основанию, BO является также высотой и биссектрисой. Значит прямая BO ⊥ AC и ∠ ABO = ∠ CBO. Теорема доказана.

 

Билет№13.

Инструкция

При определении высоты удаленного предмета, основание которого недоступно, а расстояние до него нельзя измерить непосредственно, используйте простые вычисления с приемением подручных предметов или специальных приспособлений. Первый этап – определение расстояния до объекта.

Допустим, что от предмета с неизвестной вам высотой (точка Х) вас отделяет непреодолимое препятствие, например, река. Выберите на своей стороне точку А, располагающуюся примерно напротив нужного вам объекта.

Теперь повернитесь под прямым углом вправо и сделайте 15-20 шагов. В этом месте воткните в землю ветку или палочку. Это будет точка О. Проделайте точно такое же число шагов в том же направлении. Вы получили точку В; отметьте ее также каким-либо предметом.

От точки В двигайтесь под прямым углом, удаляясь от берега. В тот момент, когда точка вашего нахождения будет располагаться между объектом (точка Х) и точкой О, остановитесь. Расстояние от вас до точки В будет равно расстоянию от первой точки (А) до точки Х, обозначаемой нужный вам объект. Измерить расстояние теперь можно шагами, а затем перевести их в метры.

Теперь, когда расстояние до объекта известно, переходите к определению его высоты. Для этого вам понадобится длинный шест или палка с вращающейся планкой. Поставьте на удалении от измеряемого объекта шест АС с вращающейся планкой и направьте ее на верхнюю точку объекта (точка С’).

 

Отметьте на поверхности земли точку В, чтобы в этой точке прямая АА' пересекалась бы с поверхностью земли. Треугольники А'С'В и АСВ будут подобными, поскольку имеют общий угол и по углу, равному 90 градусов. Из этого следует, что:
А'С' / АС = ВА' / ВА или

Высота предмета, таким образом, будет равняться:
А'С' = АС х ВА' / ВА.

Следующий способ предполагает более сложные вычисления. Допустим, вам требуется определить высоту АН удаленного предмета. Отметьте на определенном расстоянии от основания Н точку В и измерьте при помощи астролябии угол АВН, а затем по этим данным из прямоугольного треугольника АНВ найдите высоту объекта по формуле:

АН = НВ х tgАВН.

 

 

2) Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.

На рисунке — центральные и вписанные углы, а также их важнейшие свойства.

 

Тео рема о вписанном угле. Вписанный угол равен половине центрального угла,

опирающегося на ту же дугу.

Следствие . Вписанные углы, опирающиеся на одну и ту же дугу (или равные дуги),

равны.

Определение. Угловой величиной дуги называется величина опирающегося не нее

центрального угла.

1. а) Получите из теоремы о вписанном угле свойство вписанного угла, опирающегося на

диаметр.

б) Вписанный угол АВС прямой. Что можно сказать о расположении точек А и С?

в) АС – диаметр окружности, точка В не принадлежит прямой АС. Докажите, что угол АВС

является острым (прямым, тупым) тогда и только тогда, когда точка В находится вне (на,

внутри) окружности.

18. Сформулируйте и докажите теорему о вписанных углах,

опирающихся на полуокружность. Вписанный угол, опираю-

щийся на полуокружность – прямой. (Вписанный угол, опираю-

щийся на диаметр – прямой.)

Рис. 17

— AКС, — AМС, — AВС и — AFС опира-

ются на полуокружность, градусная мера

которой равна 180° (рис. 17). Так как

вписанные углы измеряются половиной

дуги на которую опираются, то

— AКС =— AМС =— AВС =— AFС = 90o

.

19. Что такое хорда окружности? Какая хорда называется

диаметром? Отрезок, соединяющий две точки окружности, назы-

вается хордой. Хорда, проходящая через центр окружности, назы-

вается диаметром.

Рис. 18

Диаметр – самая большая

хорда, любой диаметр – хорда, но не

всякая хорда является диаметром. На

рисунке 18 АВ, DE, EC, MN – хорды.

20. Сформулируйте и докажите теорему об отрезках пересе-

кающихся хорд. Следствие.

Теорема. Если две хорды окружности пересекаются, то

произведение отрезков одной хорды равно произведению отрезков

другой хорды.

Билет№5.

1.
Прямая, принадлежащая плоскости окружности и имеющая с окружностью только одну общую точку, называется касательнойк этой окружности.

Для того чтобы прямая была касательной к окружности, необходимо и достаточно, чтобы эта прямая была перпендикулярна диаметру окружности и проходила через его конец.

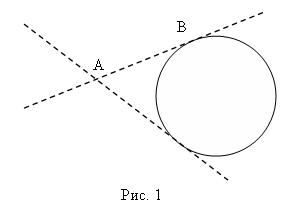
Через любую точку, лежащую вне окружности и принадлежащую плоскости окружности, можно провести две различные касательные (рис. 1).

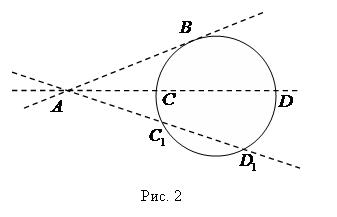
Прямая, имеющая с окружностью две общие точки, называется секущей. На рис. 2 AD и AD1 - секущие.

Если через точку A, лежащую вне круга, провести касательную в секущую (см. рис. 2), то отрезки касательной и секущей связаны равенством

∣AB∣2=∣AD∣·∣AC∣=∣ ∣ AD1∣ ∣ ·∣ ∣ AC1∣ ∣

Секущая — это прямая, которая на некотором участке пересекает в двух точках данную кривую.

Путём приближения из секущей можно получить касательную в некоторой точке P. Если секущая определяется двумя точками пересечения с данной кривой, P и Q, где положение точки P фиксировано, а положение точки Q может изменяться, то по мере того, как точка Q приближается к точке P вдоль кривой, направление секущей приближается к направлению касательной в точке P (считаем, что первая производная кривой является непрерывной в точке P, и поэтому существует только одна касательная в этой точке). Можно сказать, что по мере того, как точка Q приближается к P, наклон секущей, или направление, в пределе приближается к наклону касательной. Эта идея является основой для геометрического определения производной.

Хорда — это участок секущей, который лежит между двумя точками пересечения с кривой.

Касание — свойство двух линий или линии и поверхности иметь в некоторой точке общую касательную прямую или свойство двух поверхностей иметь в некоторой точке общую касательную плоскость.

Точка в которой две геометрические фигуры имеют касание, называется точкой касания или точкой соприкосновения.

Характеристикой близости двух линий, линии и поверхности или двух поверхностей в окрестности их общей точки является порядок касания.

[править]